A link 🔗¶
The following headline, in Everyday Health, is about a review published in July 2020 in the European Journal of Preventive Cardiology.
The following headline, in Everyday Health, is about a review published in July 2020 in the European Journal of Preventive Cardiology.
Is there any relation between chocolate consumption ๐ซ and heart disease โค๏ธ?
Association is another term for "any relation" or "link" ๐.
Researchers examined [...] a total of 336,289 participants [...] which found that eating any kind of chocolate more than once per week was linked with an 8 percent reduced risk of coronary artery disease.
Does chocolate consumption ๐ซ lead to a reduction in heart disease โค๏ธ?
This is called causation or a "causal" relation.
Other headlines about the same research article:
What can you say about the relationship between chocolate consumption ๐ซ and a reduction in heart disease โค๏ธ?
A. The data shows that there is an association and this is a causal link. Eating chocolate reduces the risk of heart disease.
B. The data shows evidence of an association but not causation.
C. The data doesn't necessarily show an association, as there could be another explanation for these results not considered here.
Not this Jon Snow...
from IPython.display import HTML
HTML('images/snow_map.html')
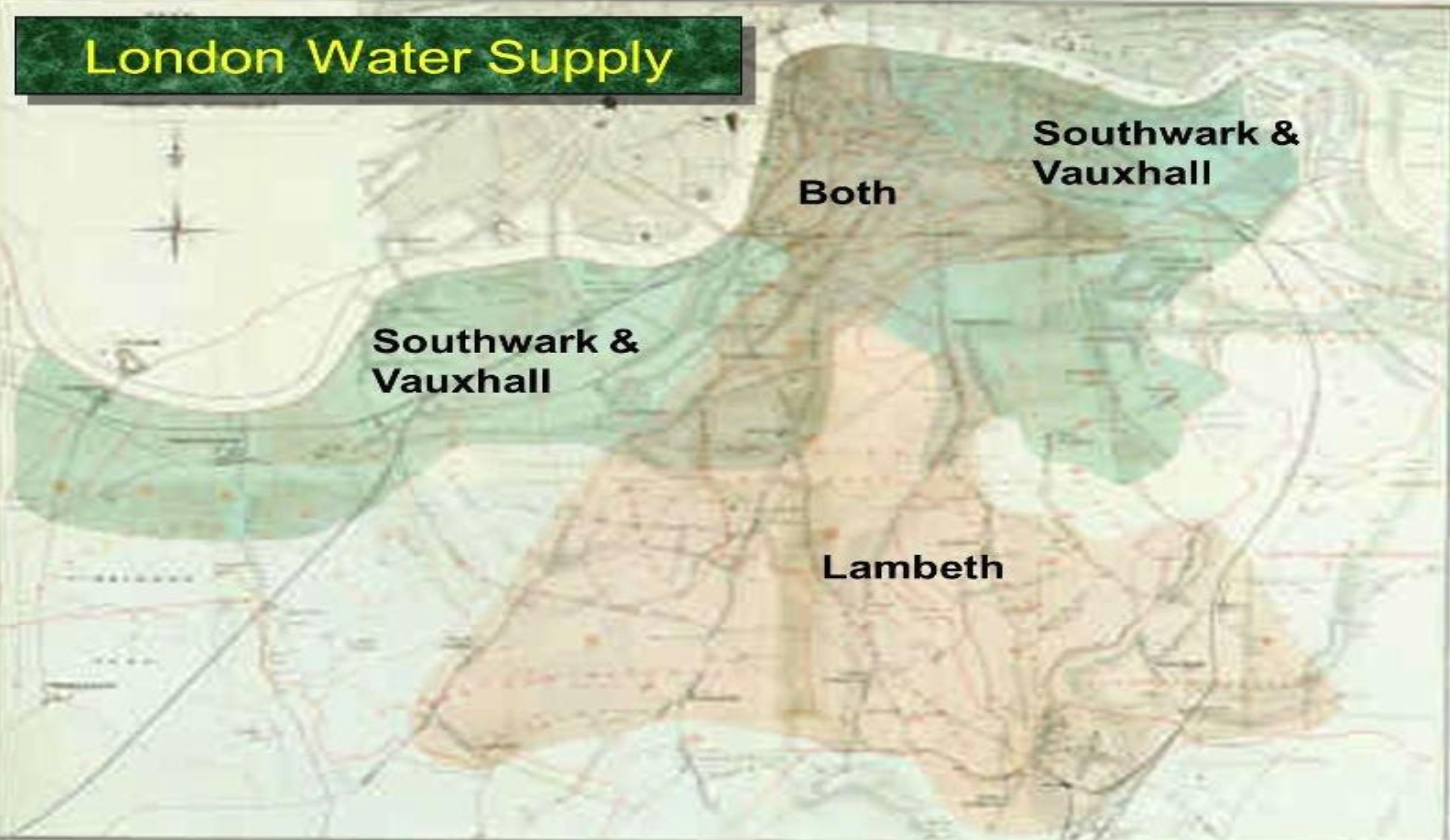
Which houses ๐ were part of the treatment group?
A. All houses in the region of overlap.
B. Houses served by S&V (dirty water) in the region of overlap.
C. Houses served by Lambeth (clean water) in the region of overlap.
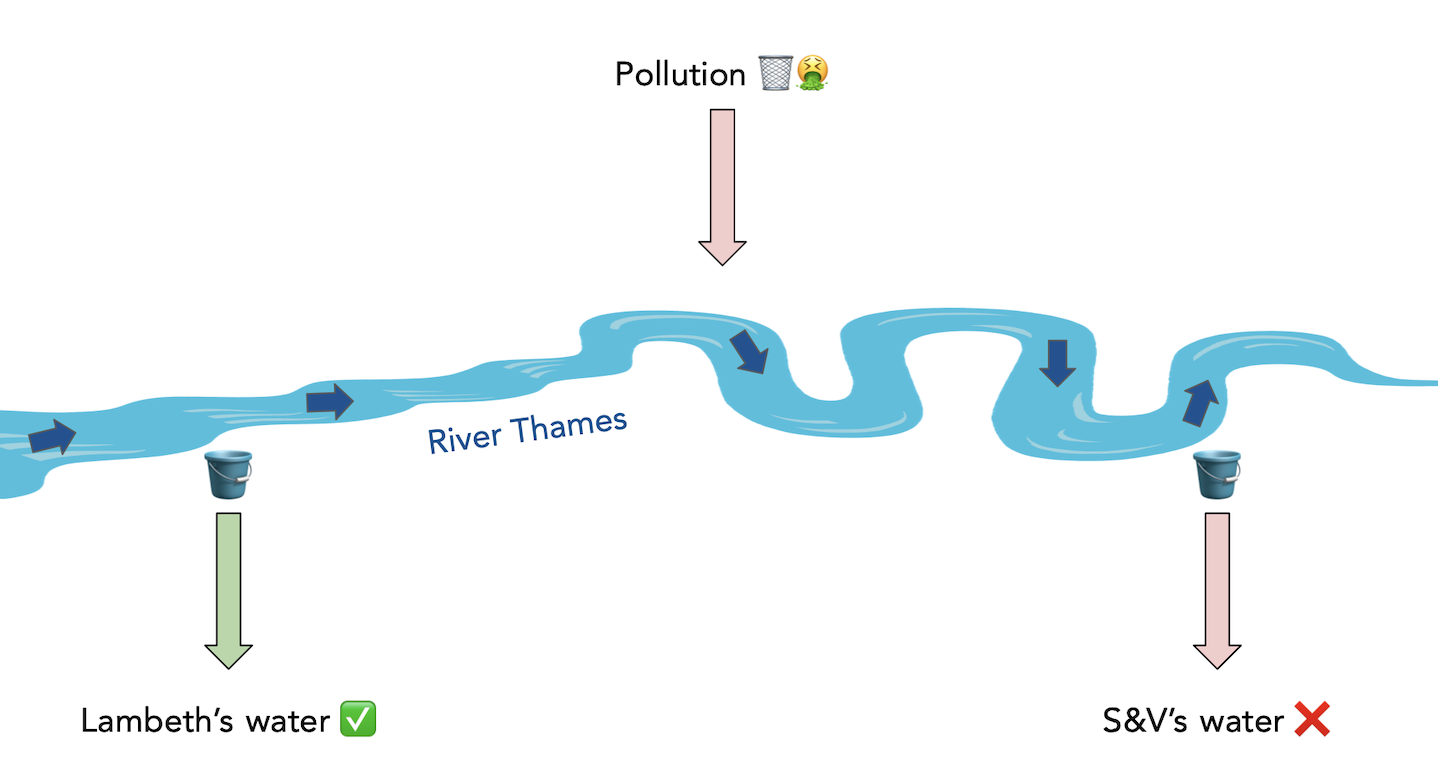
โโฆ there is no difference whatever in the houses or the people receiving the supply of the two Water Companies, or in any of the physical conditions with which they are surrounded โฆโ
In other words, the two groups were similar except for the treatment.
Snow collected this data:
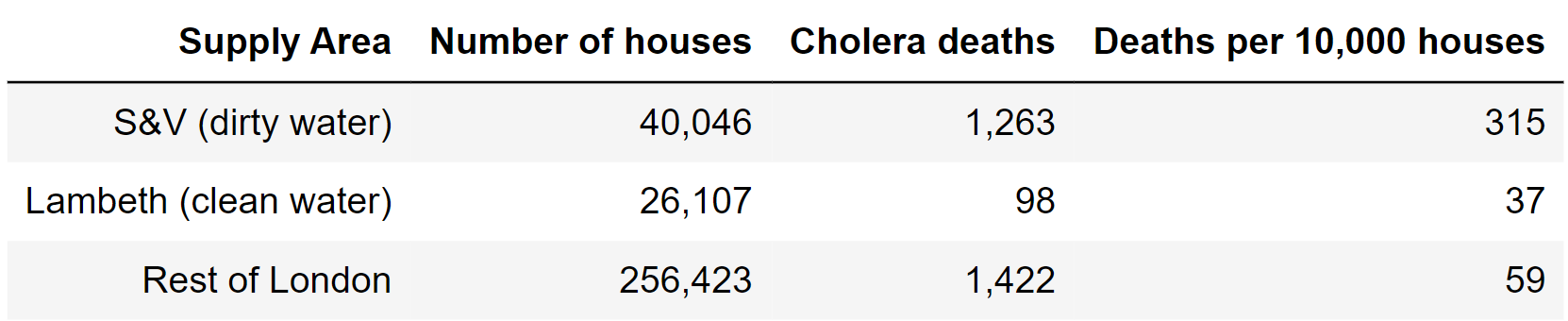
Does dirty water cause cholera?
A. Yes โ๏ธ, I think so.
B. No โ, I don't think so.
C. Maybe โ, I can't tell.
If the treatment and control groups are similar apart from the treatment, then the differences between the outcomes in the two groups can be ascribed to the treatment.
If the treatment and control groups have systematic differences other than the treatment, then it might be difficult to identify causality.
In an observational study, participants self-select or naturally fall into groups. Not controlled and not random!
Are the outcomes different because of the treatment or because of other systematic differences? ๐ Hard to tell!
These other differences are called confounding factors (confounding means confusing).
Example: previously, it was widely accepted that coffee โ caused lung cancer. Why?
If you assign individuals to the treatment and control groups at random, then the two groups are likely to be similar apart from the treatment.
You can account โ mathematically โ for variability in the assignment.
Such an experiment is known as a randomized controlled experiment (or "randomized controlled trial" or RCT).
Which of these questions would we not be able to answer by setting up a randomized controlled trial?
A. Does daily meditation ๐ reduce anxiety?
B. Does playing video games ๐ฎ increase aggressive behavior?
C. Does smoking cigarettes ๐ฌ cause weight loss?
D. Does early exposure to classical music ๐ป increase a personโs IQ?
Group by some treatment and measure some outcome.
Simplest setting: a treatment group and a control group.
If the outcome differs between these two groups, that's evidence of an association (or relation).
If, in addition, the two groups are similar in all ways but the treatment, differences in the outcome can be ascribed to the treatment. This is causation.
If the treatment and control groups have systematic differences other than the treatment itself, then it's hard to identify a causal link.
Such systematic differences are called confounding factors.
Confounding factors are often present in observational studies.
When subjects are split up randomly, it's unlikely that there will be systematic differences between the groups.
And it's possible to account for the chance of a difference.
Therefore, randomized controlled experiments are the most reliable way to establish causal relations.
On Wednesday, we'll switch gears and start programming ๐ป in Python ๐.
Further reading ๐:
