# Set up packages for lecture. Don't worry about understanding this code,
# but make sure to run it if you're following along.
import numpy as np
import babypandas as bpd
import pandas as pd

import matplotlib.pyplot as plt
from matplotlib_inline.backend_inline import set_matplotlib_formats
set_matplotlib_formats("svg")
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = (10, 5)

np.set_printoptions(threshold=20, precision=2, suppress=True)
pd.set_option("display.max_rows", 7)
pd.set_option("display.max_columns", 8)
pd.set_option("display.precision", 2)

from IPython.display import display, IFrame

def binning_animation():
    src="https://docs.google.com/presentation/d/e/2PACX-1vTnRGwEnKP2V-Z82DlxW1b1nMb2F0zWyrXIzFSpQx_8Wd3MFaf56y2_u3JrLwZ5SjWmfapL5BJLfsDG/embed?start=false&loop=false&delayms=60000&rm=minimal"
    width=900
    height=270
    display(IFrame(src, width, height))
    
import warnings
warnings.simplefilter('ignore')

Lecture 7 – Histograms and Overlaid Plots

DSC 10, Spring 2023

Announcements

• Homework 1 is due tomorrow at 11:59PM.
• Lab 2 is due on Saturday 4/22 at 11:59PM.
• Come to office hours for help! The schedule is here.
• Watch these optional extra videos from past quarters to supplement the last lecture:
  • Using str.contains().
  • How line plots work with sorting.
• Check out the new Diagrams page on the course website.

Agenda

• Distributions.
• Density histograms.
• Overlaid plots.

Today's material is quite theoretical – make sure to go to discussion this week!

Review: Types of visualizations

The type of visualization we create depends on the kinds of variables we're visualizing.

• Scatter plot: Numerical vs. numerical.
  • Example: Weight vs. height.
• Line plot: Sequential numerical (time) vs. numerical.
  • Example: Height vs. time.
• Bar chart: Categorical vs. numerical.
  • Example: Heights of different family members.
• Histogram: Distribution of numerical.

We may interchange the words "plot", "chart", and "graph"; they all mean the same thing.

Some bad visualizations

Distributions

What is the distribution of a variable?

• The distribution of a variable consists of all values of the variable that occur in the data, along with their frequencies.
• Distributions help you understand:

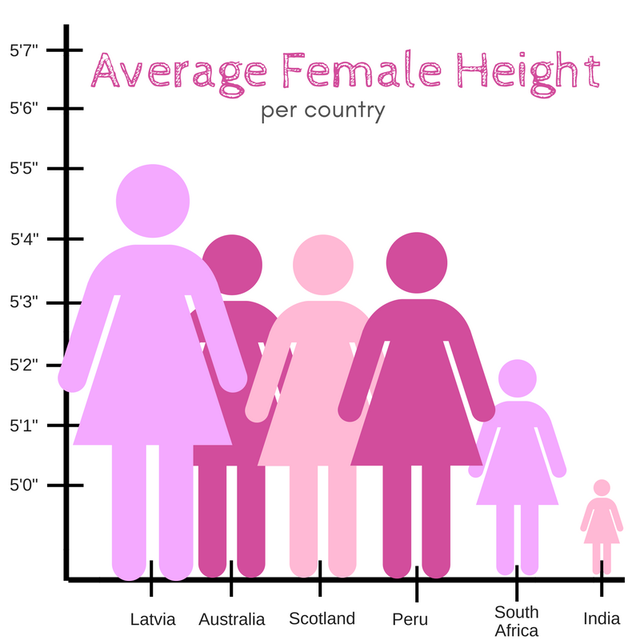
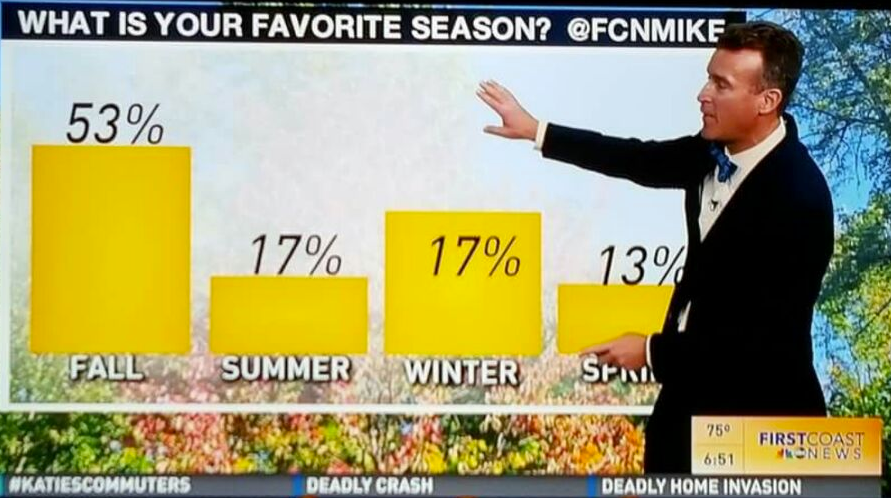
  How often does a variable take on a certain value?

• Both categorical and numerical variables have distributions.

Categorical variables

The distribution of a categorical variable can be displayed as a table or bar chart, among other ways! For example, let's look at the colleges of students enrolled in DSC 10 this quarter.

colleges = bpd.read_csv('data/colleges-sp23.csv')
colleges

	College	# Students
0	Sixth	66
1	Warren	47
2	Seventh	40
3	Marshall	37
4	Revelle	35
5	ERC	28
6	Muir	20

colleges.plot(kind='barh', x='College', y='# Students');

colleges.plot(kind='bar', x='College', y='# Students');

Recap: Top 200 songs in the US on Spotify as of Thursday (4/13/2023)

charts = (bpd.read_csv('data/regional-us-daily-2023-04-13.csv')
          .set_index('rank')
          .get(['track_name', 'artist_names', 'streams', 'uri'])
         )
charts

	track_name	artist_names	streams	uri
rank
1	Last Night	Morgan Wallen	1801636	spotify:track:7K3BhSpAxZBznislvUMVtn
2	Search & Rescue	Drake	1515162	spotify:track:7aRCf5cLOFN1U7kvtChY1G
3	Kill Bill	SZA	1412326	spotify:track:1Qrg8KqiBpW07V7PNxwwwL
...	...	...	...	...
198	Redbone	Childish Gambino	291222	spotify:track:0wXuerDYiBnERgIpbb3JBR
199	You're On Your Own, Kid	Taylor Swift	290995	spotify:track:4D7BCuvgdJlYvlX5WlN54t
200	Fall In Love	Bailey Zimmerman	290535	spotify:track:5gVCfYmQRPy1QJifP8f5gg

200 rows × 4 columns

Distribution of artists, a categorical variable

That is, how many songs does the artist with the most songs have? What about the artist with the second most songs?

First, let's create a DataFrame with a single column that describes the number of songs in the top 200 per artist. This involves using .groupby with .count(). Since we want one row per artist, we will group by 'artist_names'.

charts

	track_name	artist_names	streams	uri
rank
1	Last Night	Morgan Wallen	1801636	spotify:track:7K3BhSpAxZBznislvUMVtn
2	Search & Rescue	Drake	1515162	spotify:track:7aRCf5cLOFN1U7kvtChY1G
3	Kill Bill	SZA	1412326	spotify:track:1Qrg8KqiBpW07V7PNxwwwL
...	...	...	...	...
198	Redbone	Childish Gambino	291222	spotify:track:0wXuerDYiBnERgIpbb3JBR
199	You're On Your Own, Kid	Taylor Swift	290995	spotify:track:4D7BCuvgdJlYvlX5WlN54t
200	Fall In Love	Bailey Zimmerman	290535	spotify:track:5gVCfYmQRPy1QJifP8f5gg

200 rows × 4 columns

songs_per_artist = charts.groupby('artist_names').count()
songs_per_artist

	track_name	streams	uri
artist_names
21 Savage	1	1	1
21 Savage, Metro Boomin	2	2	2
Arctic Monkeys	2	2	2
...	...	...	...
Yng Lvcas, Peso Pluma	1	1	1
Zach Bryan	2	2	2
d4vd	2	2	2

136 rows × 3 columns

Using .assign and .drop, we'll create a column named 'count' that contains the same information that the other 3 columns contain, and then .get only that column (or equivalently, drop the other 3 columns).

# If we give .get a list, it will return a DataFrame instead of a Series!
songs_per_artist = (songs_per_artist
                    .assign(count=songs_per_artist.get('streams'))
                    .get(['count']))
songs_per_artist

	count
artist_names
21 Savage	1
21 Savage, Metro Boomin	2
Arctic Monkeys	2
...	...
Yng Lvcas, Peso Pluma	1
Zach Bryan	2
d4vd	2

136 rows × 1 columns

Let's try and create a bar chart directly.

songs_per_artist.plot(kind='barh', y='count');

That's hard to read! There are 136 bars, since there are 136 rows in songs_per_artist. To keep things concise, let's just look at the artists with at least 3 songs on the charts.

(
    songs_per_artist[songs_per_artist.get('count') >= 3]
    .sort_values('count')
    .plot(kind='barh', y='count')
);

Better!

Distribution of streams, a numerical variable

• In the previous slide, we looked at the distribution of artists; artist names are a categorical variable.
• Now, let's try and look at the distribution of the number of streams, which is a numerical variable.
• As we'll see, a bar chart is not the right choice of visualization.

# Instead of streams, we'll look at millions of streams.
charts = charts.assign(million_streams=np.round(charts.get('streams') / 1000000, 2))
charts

	track_name	artist_names	streams	uri	million_streams
rank
1	Last Night	Morgan Wallen	1801636	spotify:track:7K3BhSpAxZBznislvUMVtn	1.80
2	Search & Rescue	Drake	1515162	spotify:track:7aRCf5cLOFN1U7kvtChY1G	1.52
3	Kill Bill	SZA	1412326	spotify:track:1Qrg8KqiBpW07V7PNxwwwL	1.41
...	...	...	...	...	...
198	Redbone	Childish Gambino	291222	spotify:track:0wXuerDYiBnERgIpbb3JBR	0.29
199	You're On Your Own, Kid	Taylor Swift	290995	spotify:track:4D7BCuvgdJlYvlX5WlN54t	0.29
200	Fall In Love	Bailey Zimmerman	290535	spotify:track:5gVCfYmQRPy1QJifP8f5gg	0.29

200 rows × 5 columns

To see the distribution of the number of streams, we need to group by the 'million_streams' column.

stream_counts = charts.groupby('million_streams').count()
stream_counts = (
    stream_counts
    .assign(count=stream_counts.get('track_name'))
    .get(['count'])
)
stream_counts

	count
million_streams
0.29	4
0.30	16
0.31	11
...	...
1.41	1
1.52	1
1.80	1

55 rows × 1 columns

stream_counts.plot(kind='bar', y='count', figsize=(15,5));

The horizontal axis should be numerical (like a number line), not categorical. There should be more space between certain bars than others.

For instance, the song with the most streams has 280k more streams than any other song, but that's not clear from this plot.

Density histograms

Density histograms show the distribution of numerical variables

Instead of a bar chart, we'll visualize the distribution of a numerical variable with a density histogram. Let's see what a density histogram for 'million_streams' looks like. What do you notice about this visualization?

# Ignore the code for right now.
charts.plot(kind='hist', y='million_streams', density=True, bins=np.arange(0, 2, 0.125), ec='w');

First key idea behind histograms: Binning 🗑️

• Binning is the act of counting the number of numerical values that fall within ranges defined by two endpoints. These ranges are called “bins”.
• A value falls in a bin if it is greater than or equal to the left endpoint and less than the right endpoint.
  • [a, b): a is included, b is not.
• The width of a bin is its right endpoint minus its left endpoint.

binning_animation()

Plotting a density histogram

• Density histograms (not bar charts!) visualize the distribution of a single numerical variable by placing numbers into bins.
• To create one from a DataFrame df, use

  df.plot(
    kind='hist', 
    y=column_name,
    density=True
  )
  

• Optional but recommended: Use ec='w' to see where bins start and end more clearly.

Customizing the bins

• By default, Python will bin your data into 10 equally sized bins.
• You can specify another number of equally sized bins by setting the optional argument bins equal to some other integer value.
• You can also specify custom bin start and endpoints by setting bins equal to a list or array of bin endpoints.

# There are 10 bins by default, some of which are empty.
charts.plot(kind='hist', y='million_streams', density=True, ec='w');

charts.plot(kind='hist', y='million_streams', density=True, bins=20, ec='w');

charts.plot(kind='hist', y='million_streams', density=True,
            bins=[0, 0.5, 1, 1.5, 2],
            ec='w');

In the three histograms above, what is different and what is the same?

Observations

• The general shape of all three histograms is the same, regardless of the bins. This shape is called right-skewed.
• More bins gives a finer, more granular picture of the distribution of the variable 'million_streams'.
• The $y$-axis values seem to change a lot when we change the bins. Hang onto that thought; we'll see why shortly.

Bin details

• In a histogram, only the last bin is inclusive of the right endpoint!
• The bins you specify don't have to include all data values; data values not in any bin won't be shown in the histogram.
• For equally sized bins, use np.arange.
  • Be very careful with the endpoints.
  • For example, bins=np.arange(4) creates the bins [0, 1), [1, 2), [2, 3].
• Bins can have different sizes!

charts.plot(kind='hist', y='million_streams', density=True,
            bins=np.arange(0, 1.5, 0.1),
            ec='w');

In the above example, the top song – Last Night by Morgan Wallen – is not included because the rightmost bin is [1.3, 1.4] and Last Night had 1.8 million streams.

charts.plot(kind='hist', y='million_streams', density=True,
            bins=[0, 0.2, 0.5, 1, 1.25, 1.5, 2],
            ec='w');

In the above example, the bins have different widths!

Second key idea behind histograms: Total area is 1

• In a density histogram, the $y$-axis can be hard to interpret, but it's designed to give the histogram a very nice property:

The bars of a density histogram
have a combined total area of 1.

• Important: The area of a bar is equal to the proportion of all data points that fall into that bin.

• Proportions and percentages represent the same thing.
  • A proportion is a decimal between 0 and 1, a percentage is between 0\% and 100\%.
  • The proportion 0.34 means 34\%.

Example calculation

charts.plot(kind='hist', y='million_streams', density=True,
            bins=[0, 0.2, 0.5, 1, 1.25, 1.5, 2],
            ec='w');

Based on this histogram, what proportion of the top 200 songs had less than half a million streams?

Example calculation

• The height of the [0.2, 0.5) bar looks to be around 2.4.

• The width of the bin is 0.5 - 0.2 = 0.3.

• Therefore, using the formula for the area of a rectangle,

$$\begin{align}\text{Area} &= \text{Height} \times \text{Width} \\ &= 2.4 \times 0.3 \\ &= 0.72 \end{align}$$

• Since areas represent proportions, this means that the proportion of top 200 songs with less than half a million streams was roughly 0.72 (or 72\%).

Check the math

first_bin = charts[charts.get('million_streams') < 0.5].shape[0]
first_bin

145

first_bin / 200

0.725

This matches the result we got. (Not exactly, since we made an estimate for the height.)

Calculating heights in a density histogram

Since a bar of a histogram is a rectangle, its area is given by

$$\text{Area} = \text{Height} \times \text{Width}$$

That means

$$\text{Height} = \frac{\text{Area}}{\text{Width}} = \frac{\text{Proportion (or Percentage)}}{\text{Width}}$$

This implies that the units for height are "proportion per ($x$-axis unit)". The $y$-axis represents a sort of density, which is why we call it a density histogram.

charts.plot(kind='hist', y='million_streams', density=True,
            bins=[0, 0.2, 0.5, 1, 1.25, 1.5, 2],
            ec='w');

The $y$-axis units here are "proportion per million streams", since the $x$-axis represents millions of streams.

• Unfortunately, the $y$-axis units on the histogram always displays as "Frequency". This is wrong!
• We can fix this with plt.ylabel(...) but we usually don't.

Concept Check ✅ – Answer at cc.dsc10.com

Suppose we created a density histogram of people's shoe sizes. 👟 Below are the bins we chose along with their heights.

Bin	Height of Bar
[3, 7)	0.05
[7, 10)	0.1
[10, 12)	0.15
[12, 16]	$X$

What should the value of $X$ be so that this is a valid histogram?

A. 0.02              B. 0.05              C. 0.2              D. 0.5              E. 0.7             

Bar charts vs. histograms

Bar chart	Histogram
Shows the distribution of a categorical variable	Shows the distribution of a numerical variable
1 categorical axis, 1 numerical axis	2 numerical axes
Bars have arbitrary, but equal, widths and spacing	Horizontal axis is numerical and to scale
Lengths of bars are proportional to the numerical quantity of interest	Height measures density; areas are proportional to the proportion (percent) of individuals

🌟 Important 🌟

In this class, "histogram" will always mean a "density histogram". We will only use density histograms.

Note: It's possible to create what's called a frequency histogram where the $y$-axis simply represents a count of the number of values in each bin. While easier to interpret, frequency histograms don't have the important property that the total area is 1, so they can't be connected to probability in the same way that density histograms can. That makes them far less useful for data scientists.

Overlaid plots

Example: Populations of San Diego and San Jose over time

The data for both cities comes from macrotrends.net.

population = bpd.read_csv('data/sd-sj-2023.csv').set_index('date')
population

	Pop SD	Growth SD	Pop SJ	Growth SJ
date
1970	1209000	3.69	1009000	4.34
1971	1252000	3.56	1027000	1.78
1972	1297000	3.59	1046000	1.85
...	...	...	...	...
2021	3272000	0.65	1799000	0.45
2022	3295000	0.70	1809000	0.56
2023	3319000	0.73	1821000	0.66

54 rows × 4 columns

Recall: Line plots

population.plot(kind='line', y='Growth SD', 
                title='San Diego population growth rate', legend=False);

population.plot(kind='line', y='Growth SJ', 
                title='San Jose population growth rate', legend=False);

Notice the optional title and legend arguments. Some other useful optional arguments are figsize, xlabel, and ylabel. There are many optional arguments.

Overlaying plots

If y=column_name is omitted, all columns are plotted!

population.plot(kind='line');

Why are there only three lines shown, but four in the legend? 🤔

Selecting multiple columns at once

• To select multiple columns, use .get([column_1, ..., column_k]).
• Passing a list of column labels to .get returns a DataFrame.
  • .get([column_name]) will return a DataFrame with just one column!

growths = population.get(['Growth SD', 'Growth SJ'])
growths

	Growth SD	Growth SJ
date
1970	3.69	4.34
1971	3.56	1.78
1972	3.59	1.85
...	...	...
2021	0.65	0.45
2022	0.70	0.56
2023	0.73	0.66

54 rows × 2 columns

growths.plot(kind='line');

Plotting multiple graphs at once

Recipe:

1. .get only the columns that contain information relevant to your plot (or, equivalently, .drop all extraneous columns).
2. Specify the column for the $x$-axis (if not the index) in .plot(x=column_name).
3. Omit the y argument. Then all other columns will be plotted on a shared $y$-axis.

The same thing works for 'barh', 'bar', and 'hist', but not 'scatter'.

Another example: Heights of children and their parents 👪 📏

• The data below was collected in the late 1800s by Francis Galton.
  • He was a eugenicist and proponent of scientific racism, which is why he collected this data.
  • Today, we understand that eugenics is immoral, and that there is no scientific evidence or any other justification for racism.
• We will revisit this dataset later on in the course.
• For now, we'll only need the 'mother', and 'childHeight' columns.

mother_child = bpd.read_csv('data/galton.csv').get(['mother', 'childHeight'])
mother_child

	mother	childHeight
0	67.0	73.2
1	67.0	69.2
2	67.0	69.0
...	...	...
931	66.0	61.0
932	63.0	66.5
933	63.0	57.0

934 rows × 2 columns

Plotting overlaid histograms

alpha controls how transparent the bars are (alpha=1 is opaque, alpha=0 is transparent).

height_bins = np.arange(55, 80, 2.5)
mother_child.plot(kind='hist', density=True, ec='w',
                  alpha=0.65, bins=height_bins);

Why do children seem so much taller than their mothers?

Extra Practice

Try to answer these questions based on the overlaid histogram.

1. What proportion of children were between 70 and 75 inches tall?

2. What proportion of mothers were between 60 and 63 inches tall?

✅ Click here to see the answers to the problems above after you've tried them on your own.

Question 1 The height of the $[70, 72.5)$ bar is around $0.08$, meaning that $0.08 \cdot 2.5 = 0.2$ of children had heights in that interval. The height of the $[72.5, 75)$ bar is around $0.02$, meaning $0.02 \cdot 2.5 = 0.05$ of children had heights in that interval. Thus, the overall proportion of children who were between $70$ and $75$ inches tall was around $0.20 + 0.05 = 0.25$, or $25\%$. To verify our answer, we can run heights[(heights.get('childHeight') >= 70) & (heights.get('childHeight') < 75)].shape[0] / heights.shape[0] Question 2 We can't tell. We could try and breaking it up into the proportion of mothers in $[60, 62.5)$ and $[62.5, 63)$, but we don't know the latter. In the absence of any additional information, we can't infer about the distribution of values within a bin. For example, it could be that everyone in the interval $[62.5, 65)$ actually falls in the interval $[62.5, 63)$ - or it could be that no one does!

Summary, next time

Summary

• Histograms (not bar charts!) are used to display the distribution of a numerical variable.
• We will always use density histograms.
  • In a density histograms, the area of a bar represents the proportion (percentage) of values within its bin.
  • The total area of all bars is 1 (100%).
• We can overlay multiple line plots, bar charts, and histograms on top of one another to look at multiple relationships or distributions.

Next time

• Writing our own functions.
• Applying functions to the data in a DataFrame.