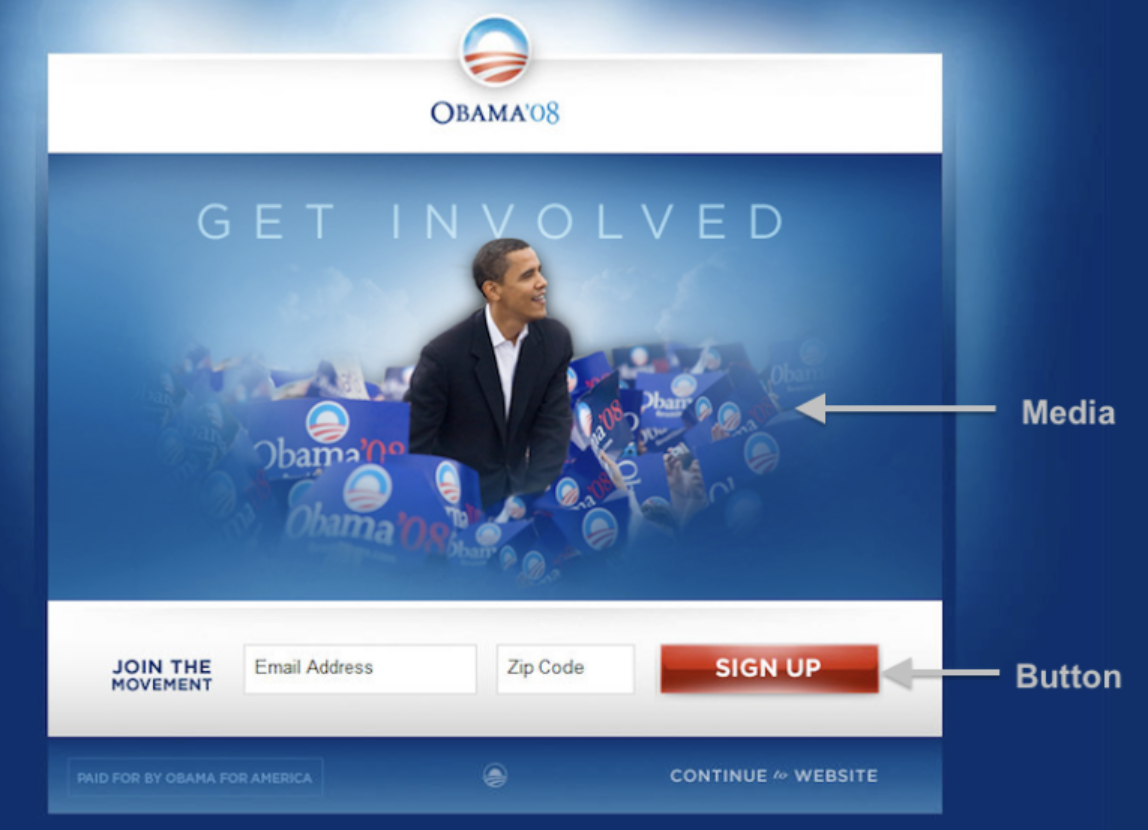
2008 Obama Campaign¶
# Set up packages for lecture. Don't worry about understanding this code,
# but make sure to run it if you're following along.
import numpy as np
import babypandas as bpd
import pandas as pd
from matplotlib_inline.backend_inline import set_matplotlib_formats
import matplotlib.pyplot as plt
set_matplotlib_formats("svg")
plt.style.use('ggplot')
np.set_printoptions(threshold=20, precision=2, suppress=True)
pd.set_option("display.max_rows", 7)
pd.set_option("display.max_columns", 8)
pd.set_option("display.precision", 2)
from IPython.display import display, IFrame, HTML
def show_permutation_testing_intro():
src="https://docs.google.com/presentation/d/e/2PACX-1vT3IfZAbqXtscEPu-nTl6lWZcXh6AWfjKsXZpWDNc0UhueXsOYQ7ivShlwbn-PW1EZm7CunTLtq7rmt/embed?start=false&loop=false&delayms=60000"
width = 960
height = 635
display(IFrame(src, width, height))
def show_permutation_testing_summary():
src = "https://docs.google.com/presentation/d/e/2PACX-1vSovXDonR6EmjrT45h4pY1mwmcKFMWVSdgpbKHC5HNTm9sbG7dojvvCDEQCjuk2dk1oA4gmwMogr8ZL/embed?start=false&loop=false&delayms=3000"
width = 960
height = 569
display(IFrame(src, width, height))
We have two distributions:
jury = bpd.DataFrame().assign(
Ethnicity=['Asian', 'Black', 'Latino', 'White', 'Other'],
Eligible=[0.15, 0.18, 0.12, 0.54, 0.01],
Panels=[0.26, 0.08, 0.08, 0.54, 0.04]
)
jury
| Ethnicity | Eligible | Panels | |
|---|---|---|---|
| 0 | Asian | 0.15 | 0.26 |
| 1 | Black | 0.18 | 0.08 |
| 2 | Latino | 0.12 | 0.08 |
| 3 | White | 0.54 | 0.54 |
| 4 | Other | 0.01 | 0.04 |
The Total Variation Distance (TVD) of two categorical distributions is the sum of the absolute differences of their proportions, all divided by 2.
def total_variation_distance(dist1, dist2):
'''Computes the TVD between two categorical distributions,
assuming the categories appear in the same order.'''
return np.abs((dist1 - dist2)).sum() / 2
jury
| Ethnicity | Eligible | Panels | |
|---|---|---|---|
| 0 | Asian | 0.15 | 0.26 |
| 1 | Black | 0.18 | 0.08 |
| 2 | Latino | 0.12 | 0.08 |
| 3 | White | 0.54 | 0.54 |
| 4 | Other | 0.01 | 0.04 |
# Calculate the TVD between the distribution of ethnicities in the eligible population
# and the distribution of ethnicities in the observed panelists
total_variation_distance(jury.get('Eligible'), jury.get('Panels'))
0.14
One way of interpreting it is as the total overrepresentation across all categories.
jury.plot(kind='barh', x='Ethnicity', figsize=(10, 5))
plt.annotate('If you add up the total amount by which the blue bars\n are longer than the red bars, you get 0.14.', (0.08, 3.9), bbox=dict(boxstyle="larrow,pad=0.3", fc="#e5e5e5", ec="black", lw=2));
plt.annotate('If you add up the total amount by which the red bars\n are longer than the blue bars, you also get 0.14!', (0.23, 0.9), bbox=dict(boxstyle="larrow,pad=0.3", fc="#e5e5e5", ec="black", lw=2));
What is the TVD between the distributions of class standing in DSC 10 and DSC 40A?
| Class Standing | DSC 10 | DSC 40A |
|---|---|---|
| Freshman | 0.45 | 0.15 |
| Sophomore | 0.35 | 0.35 |
| Junior | 0.15 | 0.35 |
| Senior+ | 0.05 | 0.15 |
Note: np.random.multinomial creates samples drawn with replacement, even though real jury panels would be drawn without replacement. However, when the sample size (1453) is small relative to the population (number of people in Alameda County), the resulting distributions will be roughly the same whether we sample with or without replacement.
eligible = jury.get('Eligible')
sample_distribution = np.random.multinomial(1453, eligible) / 1453
sample_distribution
array([0.15, 0.19, 0.14, 0.51, 0.01])
total_variation_distance(sample_distribution, eligible)
0.030708878183069534
We need to repeat the process of drawing a sample and computing the total variation distance many, many times.
tvds = np.array([])
repetitions = 10000
for i in np.arange(repetitions):
sample_distribution = np.random.multinomial(1453, eligible) / 1453
new_tvd = total_variation_distance(sample_distribution, eligible)
tvds = np.append(tvds, new_tvd)
observed_tvd = total_variation_distance(jury.get('Panels'), eligible)
bpd.DataFrame().assign(tvds=tvds).plot(kind='hist', density=True, bins=20, ec='w', figsize=(10, 5),
title='Empirical Distribution of TVD Between Eligible Population and Random Sample')
plt.axvline(observed_tvd, color='black', linewidth=4, label='Observed Statistic')
plt.legend();
np.count_nonzero(tvds >= observed_tvd) / repetitions
0.0
jury.assign(RandomSample=sample_distribution).plot(kind='barh', x='Ethnicity', figsize=(10, 5),
title="A Random Sample is Usually Similar to the Eligible Population");
So far, we've used hypothesis tests to answer questions of the form:
I have a population distribution, and I have one sample. Does this sample look like it was drawn from the population?
Consider the following form of question:
I have two samples, but no information about any population distributions. Do these samples look like they were drawn from the same population?
We can't use hypothesis testing to answer such questions yet, because all of our hypothesis tests have relied on knowing the population distribution. But what if you don't know the population distribution?
These questions are answered through A/B testing. Permutation testing is one type of A/B testing.


It is estimated that this combination of image and button brought in an additional 60 million dollars in donations versus the original version of the site.
babies = bpd.read_csv('data/baby.csv').get(['Maternal Smoker', 'Birth Weight'])
babies
| Maternal Smoker | Birth Weight | |
|---|---|---|
| 0 | False | 120 |
| 1 | False | 113 |
| 2 | True | 128 |
| ... | ... | ... |
| 1171 | True | 130 |
| 1172 | False | 125 |
| 1173 | False | 117 |
1174 rows × 2 columns
Note: The 'Birth Weight' column is measured in ounces; 100 ounces = 6.25 pounds.
smokers = babies[babies.get('Maternal Smoker')]
non_smokers = babies[babies.get('Maternal Smoker') == False]
fig, ax = plt.subplots()
baby_bins = np.arange(50, 200, 5)
non_smokers.plot(kind='hist', density=True, ax=ax, alpha=0.75, bins=baby_bins, ec='w', figsize=(10, 5))
smokers.plot(kind='hist', density=True, ax=ax, alpha=0.75, bins=baby_bins, ec='w')
plt.legend(['Maternal Smoker = False', 'Maternal Smoker = True'])
plt.xlabel('Birth Weight');
What do you notice? 👀
We recently introduced the total variation distance (TVD) as a test statistic. Why can't we use the TVD as our test statistic in this hypothesis test?
The test statistic we'll use is the difference in group means:
$$\substack{\text{mean birth weight of} \\ \text{non-smokers' babies}} \hspace{0.5in} - \hspace{0.5in} \substack{\text{mean birth weight of} \\ \text{smokers' babies}}$$Note that large values of this test statistic favor the alternative hypothesis.
Let's compute the observed statistic:
means_df = babies.groupby('Maternal Smoker').mean()
means_df
| Birth Weight | |
|---|---|
| Maternal Smoker | |
| False | 123.09 |
| True | 113.82 |
# The difference between the mean birth weight for non-smokers and smokers
means = means_df.get('Birth Weight')
observed_difference = means.loc[False] - means.loc[True]
observed_difference
9.266142572024918
show_permutation_testing_intro()
'BAC' and 'CAB' are both permutations of the string 'ABC'.'Maternal Smoker' column of babies!A permutation test is a type of A/B test (and a type of hypothesis test). It tests whether two samples come from the same population distribution. To conduct a permutation test:
Trues and Falses) to generate two new samples under the null.'Maternal Smoker' column in the babies DataFrame.df.sample returns a random sample of the rows in a DataFrame, but we want to shuffle one column independently.data = bpd.DataFrame().assign(x=['a', 'b', 'c', 'd', 'e'], y=[1, 2, 3, 4, 5])
data
| x | y | |
|---|---|---|
| 0 | a | 1 |
| 1 | b | 2 |
| 2 | c | 3 |
| 3 | d | 4 |
| 4 | e | 5 |
# The order of the rows are different,
# but each x is still in a row with the same y.
# This is NOT what we want.
data.sample(data.shape[0])
| x | y | |
|---|---|---|
| 1 | b | 2 |
| 2 | c | 3 |
| 3 | d | 4 |
| 0 | a | 1 |
| 4 | e | 5 |
np.random.permutation, which takes in a sequence and returns a shuffled version of it, as an array.# Random!
np.random.permutation(data.get('x'))
array(['b', 'd', 'e', 'a', 'c'], dtype=object)
data.assign(shuffled_x=np.random.permutation(data.get('x')))
| x | y | shuffled_x | |
|---|---|---|---|
| 0 | a | 1 | b |
| 1 | b | 2 | d |
| 2 | c | 3 | c |
| 3 | d | 4 | a |
| 4 | e | 5 | e |
As mentioned before, we'll shuffle the 'Maternal Smoker' column.
babies_with_shuffled = babies.assign(
Shuffled_Labels=np.random.permutation(babies.get('Maternal Smoker'))
)
babies_with_shuffled
| Maternal Smoker | Birth Weight | Shuffled_Labels | |
|---|---|---|---|
| 0 | False | 120 | False |
| 1 | False | 113 | True |
| 2 | True | 128 | True |
| ... | ... | ... | ... |
| 1171 | True | 130 | False |
| 1172 | False | 125 | False |
| 1173 | False | 117 | False |
1174 rows × 3 columns
Let's look at the distributions of the two new samples we just generated.
fig, ax = plt.subplots()
smokers = babies_with_shuffled[babies_with_shuffled.get('Shuffled_Labels')]
non_smokers = babies_with_shuffled[babies_with_shuffled.get('Shuffled_Labels') == False]
non_smokers.plot(kind='hist', y='Birth Weight', density=True, ax=ax, alpha=0.75, bins=baby_bins, ec='w', figsize=(10, 5))
smokers.plot(kind='hist',y='Birth Weight', density=True, ax=ax, alpha=0.75, bins=baby_bins)
plt.legend(['Maternal Smoker = False', 'Maternal Smoker = True'])
plt.xlabel('Birth Weight');
What do you notice? 👀
babies_with_shuffled.groupby('Shuffled_Labels').mean().get(['Birth Weight'])
| Birth Weight | |
|---|---|
| Shuffled_Labels | |
| False | 118.91 |
| True | 120.32 |
group_means = babies_with_shuffled.groupby('Shuffled_Labels').mean().get('Birth Weight')
group_means.loc[False] - group_means.loc[True]
-1.4047960753843114
This is the test statistic for one experiment (one "shuffle"). Let's write a function that can compute this test statistic for any shuffle.
def difference_in_group_means(weights_df):
group_means = weights_df.groupby('Shuffled_Labels').mean().get('Birth Weight')
return group_means.loc[False] - group_means.loc[True]
difference_in_group_means(babies_with_shuffled)
-1.4047960753843114
difference_in_group_means.n_repetitions = 500 # The dataset is large, so it takes too long to run if we use 5000 or 10000
differences = np.array([])
for i in np.arange(n_repetitions):
# Step 1: Shuffle the labels
shuffled_labels = np.random.permutation(babies.get('Maternal Smoker'))
# Step 2: Put them in a DataFrame
shuffled = babies_with_shuffled.assign(Shuffled_Labels=shuffled_labels)
# Step 3: Compute the difference in group means and add the result to the differences array
difference = difference_in_group_means(shuffled)
differences = np.append(differences, difference)
differences
array([-2. , -1.08, -0.45, ..., -0.78, -2.29, -0.03])
(bpd.DataFrame()
.assign(simulated_diffs=differences)
.plot(kind='hist', bins=20, density=True, ec='w', figsize=(10, 5))
);
Where does our observed statistic lie?
(bpd.DataFrame()
.assign(simulated_diffs=differences)
.plot(kind='hist', bins=20, density=True, ec='w', figsize=(10, 5))
);
plt.axvline(observed_difference, color='black', linewidth=4, label='observed difference in means')
plt.legend();
smoker_p_value = np.count_nonzero(differences >= observed_difference) / n_repetitions
smoker_p_value
0.0
show_permutation_testing_summary()
Recall, babies has two columns.
babies.take(np.arange(3))
| Maternal Smoker | Birth Weight | |
|---|---|---|
| 0 | False | 120 |
| 1 | False | 113 |
| 2 | True | 128 |
To randomly assign weights to groups, we shuffled 'Maternal Smoker' column. Could we have shuffled the 'Birth Weight' column instead?