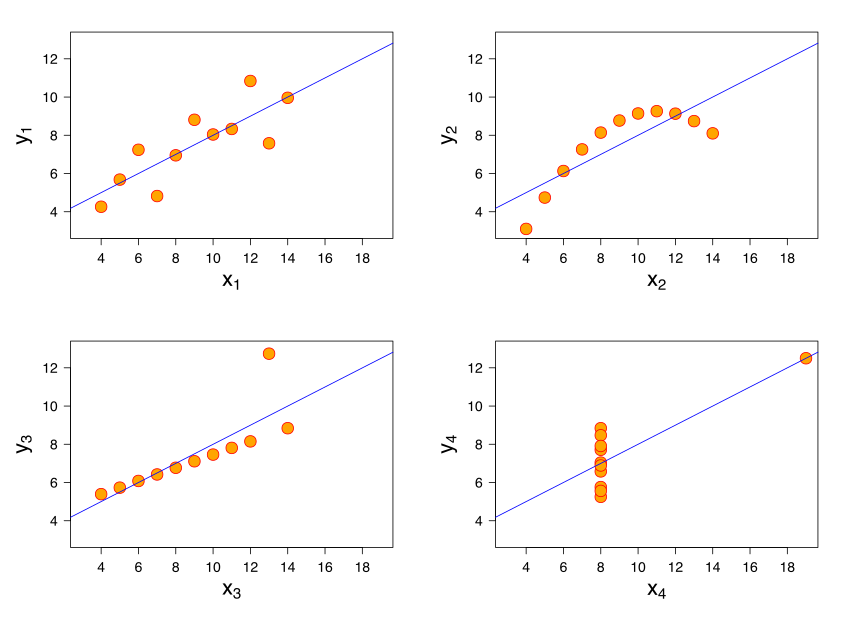
Example: Anscombe's quartet¶
# Set up packages for lecture. Don't worry about understanding this code,
# but make sure to run it if you're following along.
import numpy as np
import babypandas as bpd
import pandas as pd
from matplotlib_inline.backend_inline import set_matplotlib_formats
import matplotlib.pyplot as plt
from scipy import stats
set_matplotlib_formats("svg")
plt.style.use('ggplot')
np.set_printoptions(threshold=20, precision=2, suppress=True)
pd.set_option("display.max_rows", 7)
pd.set_option("display.max_columns", 8)
pd.set_option("display.precision", 2)
from ipywidgets import widgets
from IPython.display import clear_output, display
import warnings
warnings.filterwarnings('ignore')
def standard_units(any_numbers):
"Convert a sequence of numbers to standard units."
return (any_numbers - any_numbers.mean()) / np.std(any_numbers)
def standardize(df):
"""Return a DataFrame in which all columns of df are converted to standard units."""
df_su = bpd.DataFrame()
for column in df.columns:
df_su = df_su.assign(**{column + ' (su)': standard_units(df.get(column))})
return df_su
def correlation(df, x, y):
'''Computes the correlation between column x and column y of df.'''
return (standard_units(df.get(x)) * standard_units(df.get(y))).mean()
def slope(df, x, y):
'''Returns the slope of the regression line between columns x and y in df (in original units).'''
r = correlation(df, x, y)
return r * np.std(df.get(y)) / np.std(df.get(x))
def intercept(df, x, y):
'''Returns the intercept of the regression line between columns x and y in df (in original units).'''
return df.get(y).mean() - slope(df, x, y) * df.get(x).mean()
# All of the following code is for visualization.
def plot_regression_line(df, x, y, margin=.02, alpha=1):
'''Computes the slope and intercept of the regression line between columns x and y in df (in original units) and plots it.'''
m = slope(df, x, y)
b = intercept(df, x, y)
df.plot(kind='scatter', x=x, y=y, s=50, figsize=(10, 5), label='original data', alpha=alpha)
left = df.get(x).min()*(1 - margin)
right = df.get(x).max()*(1 + margin)
domain = np.linspace(left, right, 10)
plt.plot(domain, m*domain + b, color='orange', label='regression line', lw=4)
plt.suptitle(format_equation(m, b), fontsize=18)
plt.legend();
def format_equation(m, b):
if b > 0:
return r'$y = %.2fx + %.2f$' % (m, b)
elif b == 0:
return r'$y = %.2fx' % m
else:
return r'$y = %.2fx %.2f$' % (m, b)
np.random.seed(23)
x2 = bpd.DataFrame().assign(
x=np.arange(-6, 6.1, 0.5) + np.random.normal(size=25),
y=np.arange(-6, 6.1, 0.5)**2 + np.random.normal(size=25)
)
plot_regression_line(x2, 'x', 'y')
This line doesn't fit the data at all, despite being the "best" line for the data!
def predicted(df, x, y):
m = slope(df, x, y)
b = intercept(df, x, y)
return m * df.get(x) + b
def residual(df, x, y):
return df.get(y) - predicted(df, x, y)
Is the association between 'mom' and 'son' linear?
'mom' and 'son'?galton = bpd.read_csv('data/galton.csv')
male_children = galton[galton.get('gender') == 'male']
mom_son = bpd.DataFrame().assign(mom = male_children.get('mother'),
son = male_children.get('childHeight'))
mom_son_predictions = mom_son.assign(
predicted=predicted(mom_son, 'mom', 'son'),
residuals=residual(mom_son, 'mom', 'son'),
)
plot_regression_line(mom_son_predictions, 'mom', 'son')
idx = np.random.randint(0, mom_son_predictions.shape[0], size=50)
for i, k in enumerate(idx):
x = mom_son_predictions.get('mom').iloc[k]
y = mom_son_predictions.get('son').iloc[k]
p = mom_son_predictions.get('predicted').iloc[k]
plt.plot([x,x], [y,p], linewidth=3, color='purple', label='residuals' if i == 0 else None)
plt.legend();
print('Correlation:', correlation(mom_son, 'mom', 'son'))
Correlation: 0.32300498368490554
The residual plot of a regression line is the scatter plot with the $x$ variable on the $x$-axis and residuals on the $y$-axis.
$$\text{residual} = \text{actual } y - \text{predicted } y \text{ by regression line}$$
mom_son_predictions.plot(kind='scatter', x='mom', y='residuals', s=50, c='purple', figsize=(10, 5), label='residuals')
plt.axhline(0, linewidth=3, color='k', label='y = 0')
plt.title('Residual plot for predicting son\'s height based on mother\'s height')
plt.legend();
'mpg' to predict 'price'.hybrid = bpd.read_csv('data/hybrid.csv')
mpg_price = hybrid.assign(
predicted=predicted(hybrid, 'mpg', 'price'),
residuals=residual(hybrid, 'mpg', 'price')
)
mpg_price
| vehicle | year | price | acceleration | mpg | class | predicted | residuals | |
|---|---|---|---|---|---|---|---|---|
| 0 | Prius (1st Gen) | 1997 | 24509.74 | 7.46 | 41.26 | Compact | 32609.64 | -8099.90 |
| 1 | Tino | 2000 | 35354.97 | 8.20 | 54.10 | Compact | 19278.39 | 16076.58 |
| 2 | Prius (2nd Gen) | 2000 | 26832.25 | 7.97 | 45.23 | Compact | 28487.75 | -1655.50 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 150 | C-Max Energi Plug-in | 2013 | 32950.00 | 11.76 | 43.00 | Midsize | 30803.06 | 2146.94 |
| 151 | Fusion Energi Plug-in | 2013 | 38700.00 | 11.76 | 43.00 | Midsize | 30803.06 | 7896.94 |
| 152 | Chevrolet Volt | 2013 | 39145.00 | 11.11 | 37.00 | Compact | 37032.62 | 2112.38 |
153 rows × 8 columns
# Plot of the original data and regression line.
plot_regression_line(hybrid, 'mpg', 'price');
print('Correlation:', correlation(hybrid, 'mpg', 'price'))
Correlation: -0.5318263633683789
# Residual plot.
mpg_price.plot(kind='scatter', x='mpg', y='residuals', figsize=(10, 5), s=50, color='purple', label='residuals')
plt.axhline(0, linewidth=3, color='k', label='y = 0')
plt.title('Residual plot for regression between mpg and price')
plt.legend();
Note that as 'mpg' increases, the residuals go from being mostly large, to being mostly small, to being mostly large again. That's a pattern!
'mpg' and 'acceleration' ⛽¶'mpg' given 'acceleration'.accel_mpg = hybrid.assign(
predicted=predicted(hybrid, 'acceleration', 'mpg'),
residuals=residual(hybrid, 'acceleration', 'mpg')
)
accel_mpg
| vehicle | year | price | acceleration | mpg | class | predicted | residuals | |
|---|---|---|---|---|---|---|---|---|
| 0 | Prius (1st Gen) | 1997 | 24509.74 | 7.46 | 41.26 | Compact | 43.29 | -2.03 |
| 1 | Tino | 2000 | 35354.97 | 8.20 | 54.10 | Compact | 41.90 | 12.20 |
| 2 | Prius (2nd Gen) | 2000 | 26832.25 | 7.97 | 45.23 | Compact | 42.33 | 2.90 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 150 | C-Max Energi Plug-in | 2013 | 32950.00 | 11.76 | 43.00 | Midsize | 35.17 | 7.83 |
| 151 | Fusion Energi Plug-in | 2013 | 38700.00 | 11.76 | 43.00 | Midsize | 35.17 | 7.83 |
| 152 | Chevrolet Volt | 2013 | 39145.00 | 11.11 | 37.00 | Compact | 36.40 | 0.60 |
153 rows × 8 columns
# Plot of the original data and regression line.
plot_regression_line(accel_mpg, 'acceleration', 'mpg')
print('Correlation:', correlation(accel_mpg, 'acceleration', 'mpg'))
Correlation: -0.5060703843771185
# Residual plot.
accel_mpg.plot(kind='scatter', x='acceleration', y='residuals', figsize=(10, 5), s=50, color='purple', label='residuals')
plt.axhline(0, linewidth=3, color='k', label='y = 0')
plt.title('Residual plot for regression between acceleration and mpg')
plt.legend();
Note that the residuals tend to vary more for smaller accelerations than they do for larger accelerations – that is, the vertical spread of the plot is not similar at all points on the $x$-axis.

dino = bpd.read_csv('data/Datasaurus_data.csv')
dino
| x | y | |
|---|---|---|
| 0 | 55.38 | 97.18 |
| 1 | 51.54 | 96.03 |
| 2 | 46.15 | 94.49 |
| ... | ... | ... |
| 139 | 50.00 | 95.77 |
| 140 | 47.95 | 95.00 |
| 141 | 44.10 | 92.69 |
142 rows × 2 columns
correlation(dino, 'x', 'y')
-0.06447185270095165
slope(dino, 'x', 'y')
-0.103582502432656
intercept(dino, 'x', 'y')
53.4529784492292
plot_regression_line(dino, 'x', 'y');
Takeaway: Never trust summary statistics alone; always visualize your data!

What strategy will help us assess how different our regression line's predictions would have been if we'd used a different sample?
Don't scroll pass this point without answering!
We want to come up with a range of reasonable values for a prediction for a single input $x$. To do so, we'll:
The resulting interval will be called a prediction interval.
Note that each time we run this cell, the resulting line is slightly different!
# Step 1: Resample the dataset.
resample = mom_son.sample(mom_son.shape[0], replace=True)
# Step 2: Compute the slope and intercept of the regression line for that resample.
plot_regression_line(resample, 'mom', 'son', alpha=0.5)
plt.ylim([60, 80])
plt.xlim([57, 72]);
m_orig = slope(mom_son, 'mom', 'son')
b_orig = intercept(mom_son, 'mom', 'son')
boot_slopes = np.array([])
boot_intercepts = np.array([])
for i in np.arange(5000):
# Step 1: Resample the dataset.
resample = mom_son.sample(mom_son.shape[0], replace=True)
# Step 2: Compute the slope and intercept of the regression line for that resample.
m = slope(resample, 'mom', 'son')
b = intercept(resample, 'mom', 'son')
boot_slopes = np.append(boot_slopes, m)
boot_intercepts = np.append(boot_intercepts, b)
Using the original dataset, and hence the original slope and intercept, we get a single prediction for the input of 68.
pred_orig = m_orig * 68 + b_orig
pred_orig
70.68219686848828
Using the bootstrapped slopes and intercepts, we get an interval of predictions for the input of 68.
m_orig
0.36506116024257595
boot_slopes
array([0.33, 0.36, 0.42, ..., 0.33, 0.33, 0.4 ])
b_orig
45.85803797199311
boot_intercepts
array([48.18, 46.26, 42.22, ..., 48.02, 48.13, 43.57])
boot_preds = boot_slopes * 68 + boot_intercepts
boot_preds
array([70.74, 70.53, 70.98, ..., 70.6 , 70.88, 70.8 ])
l = np.percentile(boot_preds, 2.5)
r = np.percentile(boot_preds, 97.5)
[l, r]
[70.21553543791688, 71.159837647376]
bpd.DataFrame().assign(
predictions=boot_preds
).plot(kind='hist', density=True, bins=20, figsize=(10, 5), ec='w', title='Interval of predicted heights for the son of a 68 inch tall mother')
plt.plot([l,r],[0.01,0.01], c='gold', linewidth=10, zorder=1, label='95% prediction interval')
plt.legend();
Here, we'll plot several of our bootstrapped lines. What do you notice?
# Don't worry about the code for this.
plt.figure(figsize=(10, 5))
x = np.arange(50, 80)
ys = []
for i, (m, b) in enumerate(zip(boot_slopes[:50], boot_intercepts)):
ys.append(m * x + b)
fig = plt.plot(x, m * x + b, linewidth=1)
Observations:
# Don't worry about how this code works.
def pred_interval(mom):
plt.figure(figsize=(10, 5))
x = np.arange(50, 80)
ys = []
for i, (m, b) in enumerate(zip(boot_slopes[:50], boot_intercepts)):
ys.append(m * x + b)
plt.plot(x, m * x + b, linewidth=1, alpha=0.1)
boot_preds = boot_slopes * mom + boot_intercepts
l = np.percentile(boot_preds, 2.5)
r = np.percentile(boot_preds, 97.5)
plt.plot([mom, mom], [l, r], linewidth=5, color='#eb7e35', label='95% prediction interval')
plt.xlim(50, 80)
plt.ylim(62, 77)
plt.title(f'95% prediction interval for the height of a son whose mother is {mom} inches tall: {[np.round(l, 3), np.round(r, 3)]}')
plt.legend()
plt.show()
def slider_widget():
mom_slider = widgets.IntSlider(value=64, min=50, max=78, step=1, description="mom's height")
ui = widgets.HBox([mom_slider])
out = widgets.interactive_output(pred_interval, {'mom': mom_slider})
display(ui, out)
slider_widget()
HBox(children=(IntSlider(value=64, description="mom's height", max=78, min=50),))
Output()
Note that the closer a mother's height is to the mean mother's height, the narrower the prediction interval for her son's height is!