Why Python?¶
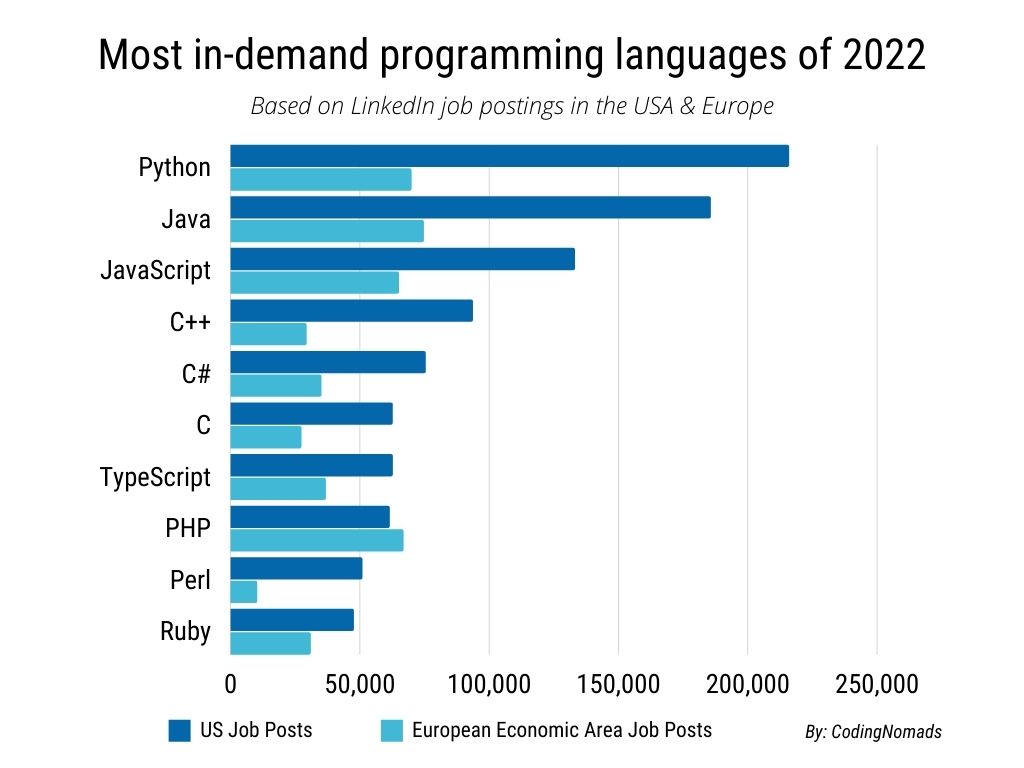
- Popular.
- Variety of uses.
- Web development.
- Data science and machine learning.
- Not really used for developing applications.
- Easy to dive right in!
# Don't worry about what this code does, but make sure to run it if you're following along.
from IPython.display import IFrame
def show_nested_eval():
src = 'https://docs.google.com/presentation/d/e/2PACX-1vQpW0NzwT3LjZsIIDAgtSMRM1cl41Gp_Lf8k9GT-gm5sGAIynw4rsgiEFbIybClD6QtxarKaVKLbR9U/embed?start=false&loop=false&delayms=60000" frameborder="0" width="960" height="569" allowfullscreen="true" mozallowfullscreen="true" webkitallowfullscreen="true"'
width = 960
height = 569
return IFrame(src, width, height)
Lots of programming – follow along in the notebook by clicking the "Expressions and Data Types" link on the course website.

 This button!
This button!shift + enter (or shift + return) on your keyboard (strongly preferred), or17
17
-1 + 3.14
2.14
2 ** 3
8
(17 - 14) / 2
1.5
# Only one value is displayed. Why?
3 * 4
5
5
| Operation | Operator | Example | Value |
|---|---|---|---|
| Addition | + |
2 + 3 |
5 |
| Subtraction | - |
2 - 3 |
-1 |
| Multiplication | * |
2 * 3 |
6 |
| Division | / |
7 / 3 |
2.66667 |
| Remainder | % |
7 % 3 |
1 |
| Exponentiation | ** |
2 ** 0.5 |
1.41421 |
3 * 2 ** 2
12
(3 * 2) ** 2
36
In the cell below, replace the ellipses with an expression that's equivalent to
$$(19 + 6 \cdot 3) - 15 \cdot \left(\sqrt{100} \cdot \frac{1}{30}\right) \cdot \frac{3}{5} + \frac{4^2}{2^3} + \left( 6 - \frac{2}{3} \right) \cdot 12 $$Try to use parentheses only when necessary.
...
Ellipsis
Below, we compute the number of seconds in a year.
60 * 60 * 24 * 365
31536000
If we want to use the above value later in our notebook to find, say, the number of seconds in 12 years, we'd have to copy-and-paste the expression. This is inconvenient, and prone to introducing errors.
60 * 60 * 24 * 365 * 12
378432000
It would be great if we could store the initial value and refer to it later on!
= symbol.= symbol is evaluated before being assigned to the name on the left-hand side.myvariable is bound to 5 (value) not 2 + 3 (expression).Note that before we use it in an assignment statement, more_than_1 has no meaning.
more_than_1
--------------------------------------------------------------------------- NameError Traceback (most recent call last) /var/folders/ch/hyjw6whx3g9gshnp58738jc80000gp/T/ipykernel_2277/3210039468.py in <module> ----> 1 more_than_1 NameError: name 'more_than_1' is not defined
After using it in an assignment statement, we can ask Python for its value.
# Note that an assignment statement doesn't output anything!
more_than_1 = 15 - 5
more_than_1
10
Any time we use more_than_1 in an expression, 10 is substituted for it.
more_than_1 * 2
20
Note that the above expression did not change the value of more_than_1, because we did not re-assign more_than_1!
more_than_1
10
The following assignment statements are valid, but use poor variable names 😕.
six = 15
i_45love_chocolate_9999 = 60 * 60 * 24 * 365
The following assignment statements are valid, and use good variable names ✅.
seconds_per_hour = 60 * 60
hours_per_year = 24 * 365
seconds_per_year = seconds_per_hour * hours_per_year
The following "assignment statements" are invalid ❌.
6 = 15
File "/var/folders/ch/hyjw6whx3g9gshnp58738jc80000gp/T/ipykernel_2277/2046484920.py", line 1 6 = 15 ^ SyntaxError: cannot assign to literal
3 = 2 + 1
File "/var/folders/ch/hyjw6whx3g9gshnp58738jc80000gp/T/ipykernel_2277/2449763097.py", line 1 3 = 2 + 1 ^ SyntaxError: cannot assign to literal
= to the value to the right of =, nothing more.x = 3
x
4 = x
uc = 2
sd = 3 + uc
Assignment statements are not promises – the value of a variable can change!
uc = 7
Note that even after changing uc, we did not change sd, so it is still the same as before.
sd
5
Assume you have run the following three lines of code:
side_length = 5
area = side_length ** 2
side_length = side_length + 2
What are the values of side_length and area after execution?
A. side_length = 5, area = 25
B. side_length = 5, area = 49
C. side_length = 7, area = 25
D. side_length = 7, area = 49
E. None of the above
tab to autocomplete a set name¶...
Ellipsis
abs(-12)
12
max(3, -4)
3
max(2, -3, -6, 10, -4)
10
# Only two arguments!
max(4 + 5, 5 - 4)
9
? after a function to see the documentation for a function¶Or, use the help function, e.g. help(max).
max?
round¶my_number = 1.22
round(my_number)
1
round?
round(1.22222, 3)
1.222
We can nest many function calls to evaluate sophisticated expressions.
min(abs(max(-1, -2, -3, min(4, -2))), max(5, 100))
1
...how did that work?
show_nested_eval()
module.function(), called "dot notation".import math¶sqrt, log, pow, etc.
import math
math.sqrt(9)
3.0
math.pow(3, 2)
9.0
# What base is log?
math.log?http://localhost:8888/notebooks/Documents/GitHub/dsc10-2023-wi-private/lectures/lec02/lec02.ipynb#
# Tab completion for browsing
math.
File "/var/folders/ch/hyjw6whx3g9gshnp58738jc80000gp/T/ipykernel_2277/3814339723.py", line 2 math. ^ SyntaxError: invalid syntax
It also has constants built-in!
math.pi
3.141592653589793
Assume you have run the following statements:
x = 3
y = -2
Which of these examples results in an error?
A. abs(x, y)
B. math.pow(x, abs(y))
C. round(x, max(abs(y ** 2)))
D. math.pow(x, math.pow(y, x))
E. More than one of the above
4 / 2
2.0
5 - 3
2
To us, 2.0 and 2 are the same number, $2$. But to Python, these appear to be different!
type function to check a value's type.int and float¶int : An integer of any size.float: A number with a decimal point.int¶ints (+, -, *, **), the result will be another int.ints have arbitrary precision in Python, meaning that your calculations will always be exact. 3 + 5
8
type(3 + 5)
int
2 ** 300
2037035976334486086268445688409378161051468393665936250636140449354381299763336706183397376
2 ** 3000
1230231922161117176931558813276752514640713895736833715766118029160058800614672948775360067838593459582429649254051804908512884180898236823585082482065348331234959350355845017413023320111360666922624728239756880416434478315693675013413090757208690376793296658810662941824493488451726505303712916005346747908623702673480919353936813105736620402352744776903840477883651100322409301983488363802930540482487909763484098253940728685132044408863734754271212592471778643949486688511721051561970432780747454823776808464180697103083861812184348565522740195796682622205511845512080552010310050255801589349645928001133745474220715013683413907542779063759833876101354235184245096670042160720629411581502371248008430447184842098610320580417992206662247328722122088513643683907670360209162653670641130936997002170500675501374723998766005827579300723253474890612250135171889174899079911291512399773872178519018229989376
float¶float is specified using a decimal point.float might be printed using scientific notation.2.0 + 3.2
5.2
type(2.0 + 3.2)
float
2.0 ** 300
2.037035976334486e+90
float¶floats have limited size (but the limit is huge).floats have limited precision of 15-16 decimal places.1 + 0.2
1.2
1 + 0.1 + 0.1
1.2000000000000002
2.0 ** 3000
--------------------------------------------------------------------------- OverflowError Traceback (most recent call last) /var/folders/ch/hyjw6whx3g9gshnp58738jc80000gp/T/ipykernel_2277/1310821553.py in <module> ----> 1 2.0 ** 3000 OverflowError: (34, 'Result too large')
int and float¶int to a float in a mixed expression involving both types.ints automatically returns a float value.int and float functions.2.0 + 3
5.0
2 / 1
2.0
# Want an integer back
int(2 / 1)
2
# int chops off the decimal point, effectively rounding DOWN
int(3.9)
3

Our notebook still remembers all of the variables we defined earlier in the lecture.
more_than_1
10
ints and floats are numbers.ints are integers, while floats contain decimal points.Note: We will introduce some code in labs and homeworks as well. Not everything will be in lecture. You will learn by doing!