# Run this cell to set up packages for lecture.
from lec25_imports import *
Announcements¶
- Discussion 8 is today at 4PM, 5PM, and 7PM in Solis 104.
- Remember you don't have to go to every discussion to get full participation credit.
- Thanksgiving holiday: no course meetings or office hours on Thursday or Friday. Happy Thanksgiving! 🦃
- The Final Project is due Tuesday at 11:59PM.
- New submission instructions: In addition to submitting the Jupyter notebook (.ipynb file), you'll also need to submit a PDF of your notebook. There will be two separate Gradescope submissions for the two different file types; please submit to both!
Agenda¶
- The regression line in standard units.
- The regression line in original units.
- Outliers.
- Errors in prediction.
The regression line in standard units¶
Example: Predicting heights 👪 📏¶
Recall, in the last lecture, we aimed to use a mother's height to predict her adult son's height.
galton = bpd.read_csv('data/galton.csv')
male_children = galton[galton.get('gender') == 'male']
mom_son = bpd.DataFrame().assign(mom = male_children.get('mother'),
son = male_children.get('childHeight'))
mom_son
| mom | son | |
|---|---|---|
| 0 | 67.0 | 73.2 |
| 4 | 66.5 | 73.5 |
| 5 | 66.5 | 72.5 |
| ... | ... | ... |
| 925 | 60.0 | 66.0 |
| 929 | 66.0 | 64.0 |
| 932 | 63.0 | 66.5 |
481 rows × 2 columns
mom_son.plot(kind='scatter', x='mom', y='son', figsize=(10, 5));
Correlation¶
Recall, the correlation coefficient $r$ of two variables $x$ and $y$ is defined as the
- average value of the
- product of $x$ and $y$
- when both are measured in standard units.
def standard_units(col):
return (col - col.mean()) / np.std(col)
def calculate_r(df, x, y):
'''Returns the average value of the product of x and y,
when both are measured in standard units.'''
x_su = standard_units(df.get(x))
y_su = standard_units(df.get(y))
return (x_su * y_su).mean()
r_mom_son = calculate_r(mom_son, 'mom', 'son')
r_mom_son
0.3230049836849053
The regression line¶
- The regression line is the line through $(0,0)$ with slope $r$, when both variables are measured in standard units.
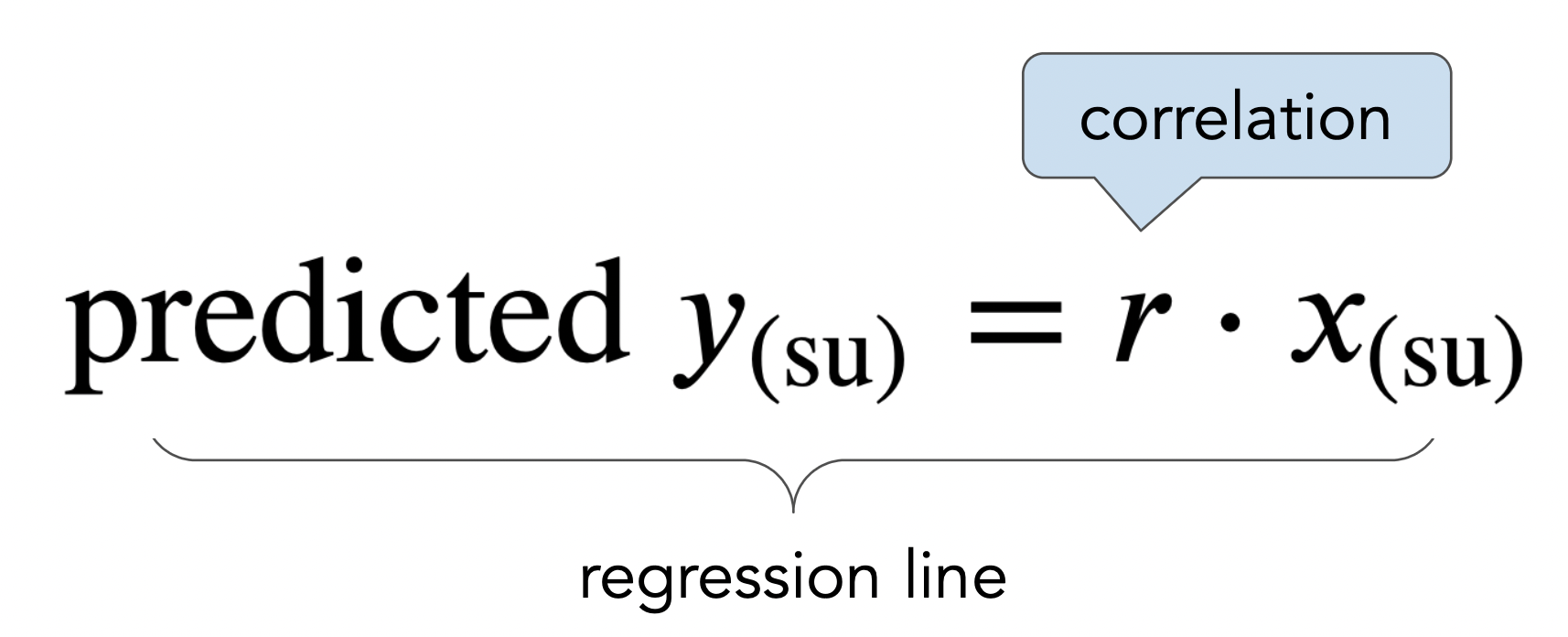
- We use the regression line to make predictions!
- Example: If a mother's height is 0.5 SDs above the average mother's height, and $r = 0.32$, our prediction is that her son's height will be $0.5 \cdot 0.32 = 0.16$ SDs above the average son's height.
- Issue: To use this form of the regression line, we need to know mothers' heights in standard units, but it would be more convenient to think in terms of inches.
Concept Check ✅ – Answer at cc.dsc10.com¶
A course has a midterm (mean 80, standard deviation 15) and a really hard final (mean 50, standard deviation 12).
If the scatter plot comparing midterm & final scores for students looks linearly associated with correlation 0.75, then what is the predicted final exam score for a student who received a 90 on the midterm?
- A. 54
- B. 56
- C. 58
- D. 60
- E. 62
The regression line in original units¶
Reflection¶
Each time we want to predict the height of an adult son given the height of his mother, we have to:
- Convert the mother's height from inches to standard units.
- Multiply by the correlation coefficient to predict the son's height in standard units.
- Convert the son's predicted height from standard units back to inches.
This is inconvenient – wouldn't it be great if we could express the regression line itself in inches?
From standard units to original units¶
When $x$ and $y$ are in standard units, the regression line is given by

What is the regression line when $x$ and $y$ are in their original units (e.g. inches)?
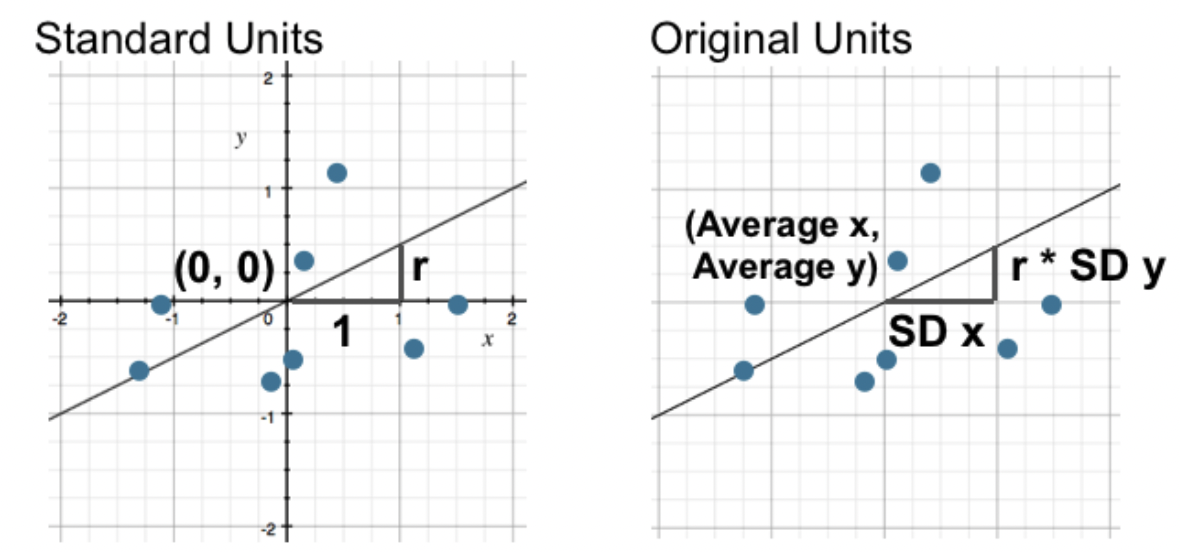
The regression line in original units¶
- We can work backwards from the relationship $$\text{predicted } y_{\text{(su)}} = r \cdot x_{\text{(su)}}$$ to find the line in original units.
$$\frac{\text{predicted } y - \text{mean of }y}{\text{SD of }y} = r \cdot \frac{x - \text{mean of } x}{\text{SD of }x}$$
- Note that $r, \text{mean of } x$, $\text{mean of } y$, $\text{SD of } x$, and $\text{SD of } y$ are constants – if you have a DataFrame with two columns, you can determine all 5 values.
- Re-arranging the above equation into the form $\text{predicted } y = mx + b$ yields the formulas:
$$\boxed{m = r \cdot \frac{\text{SD of } y}{\text{SD of }x}, \: \: b = \text{mean of } y - m \cdot \text{mean of } x}$$
- $m$ is the slope of the regression line and $b$ is the intercept.
Let's implement these formulas in code and try them out.
def slope(df, x, y):
"Returns the slope of the regression line between columns x and y in df (in original units)."
r = calculate_r(df, x, y)
return r * np.std(df.get(y)) / np.std(df.get(x))
def intercept(df, x, y):
"Returns the intercept of the regression line between columns x and y in df (in original units)."
return df.get(y).mean() - slope(df, x, y) * df.get(x).mean()
Below, we compute the slope and intercept of the regression line between mothers' heights and sons' heights (in inches).
m_heights = slope(mom_son, 'mom', 'son')
m_heights
0.3650611602425757
b_heights = intercept(mom_son, 'mom', 'son')
b_heights
45.8580379719931
So, the regression line is
$$\text{predicted son's height in inches} = 0.365 \cdot \text{mother's height in inches} + 45.858$$
Making predictions¶
def predict_son(mom):
return m_heights * mom + b_heights
What's the predicted height of a son whose mother is 62 inches tall?
predict_son(62)
68.4918299070328
What if the mother is 55 inches tall? 73 inches tall?
predict_son(55)
65.93640178533477
predict_son(73)
72.50750266970113
xs = np.arange(57, 72)
ys = predict_son(xs)
mom_son.plot(kind='scatter', x='mom', y='son', figsize=(10, 5), title='Regression line predictions, in original units', label='original data');
plt.plot(xs, ys, color='orange', lw=4, label='regression line')
plt.legend();
Outliers¶
The effect of outliers on correlation¶
Consider the dataset below. What is the correlation between $x$ and $y$?
outlier = bpd.read_csv('data/outlier.csv')
outlier.plot(kind='scatter', x='x', y='y', s=100, figsize=(10, 5));
calculate_r(outlier, 'x', 'y')
-0.02793982443854448
plot_regression_line(outlier, 'x', 'y')
Removing the outlier¶
without_outlier = outlier[outlier.get('y') > 40]
calculate_r(without_outlier, 'x', 'y')
0.9851437295364018
plot_regression_line(without_outlier, 'x', 'y')
Takeaway: Even a single outlier can have a massive impact on the correlation, and hence the regression line. Look for these before performing regression. Always visualize first!
Errors in prediction¶
Motivation¶
- We've presented the regression line in standard units as the line through the origin with slope $r$, given by $\text{predicted } y_{\text{(su)}} = r \cdot x_{\text{(su)}}$. Then, we used this equation to find a formula for the regression line in original units.
- In examples we've seen so far, the regression line seems to fit our data pretty well.
- But how well?
- What makes the regression line good?
- Would another line be better?
Example: Without the outlier¶
outlier.plot(kind='scatter', x='x', y='y', s=100, figsize=(10, 5));
m_no_outlier = slope(without_outlier, 'x', 'y')
b_no_outlier = intercept(without_outlier, 'x', 'y')
m_no_outlier, b_no_outlier
(0.9759277157245881, 3.042337135297416)
plot_errors(without_outlier, m_no_outlier, b_no_outlier)
We think our regression line is pretty good because most data points are pretty close to the regression line. The red lines are quite short.
Measuring the error in prediction¶
$$\text{error} = \text{actual value} - \text{prediction}$$
- A good prediction line is one where the errors tend to be small.
- To measure the rough size of the errors, for a particular set of predictions:
- Square the errors so that they don't cancel each other out.
- Take the mean of the squared errors.
- Take the square root to fix the units.
- This is called root mean square error (RMSE).
- Notice the similarities to computing the SD!
Root mean squared error (RMSE) of the regression line's predictions¶
without_outlier
| x | y | |
|---|---|---|
| 0 | 50 | 53.53 |
| 1 | 55 | 54.21 |
| 2 | 60 | 65.65 |
| ... | ... | ... |
| 6 | 80 | 79.61 |
| 7 | 85 | 88.17 |
| 8 | 90 | 91.05 |
9 rows × 2 columns
First, let's compute the regression line's predictions for the entire dataset.
predicted_y = m_no_outlier * without_outlier.get('x') + b_no_outlier
predicted_y
array([51.84, 56.72, 61.6 , 66.48, 71.36, 76.24, 81.12, 86. , 90.88])
To find the RMSE, we need to start by finding the errors and squaring them.
# Errors.
without_outlier.get('y') - predicted_y
0 1.69
1 -2.51
2 4.06
...
6 -1.51
7 2.18
8 0.18
Name: y, Length: 9, dtype: float64
# Squared errors.
(without_outlier.get('y') - predicted_y) ** 2
0 2.86
1 6.31
2 16.45
...
6 2.27
7 4.74
8 0.03
Name: y, Length: 9, dtype: float64
Now, we need to find the mean of the squared errors, and take the square root of that. The result is the RMSE of the regression line's predictions.
# Mean squared error.
((without_outlier.get('y') - predicted_y) ** 2).mean()
4.823770221019627
# Root mean squared error.
np.sqrt(((without_outlier.get('y') - predicted_y) ** 2).mean())
2.1963083164755415
The RMSE of the regression line's predictions is about 2.2. Is this big or small, relative to the predictions of other lines? 🤔
Root mean squared error (RMSE) in an arbirtrary line's predictions¶
- We've been using the regression line to make predictions. But we could use a different line!
- To make a prediction for
xusing an arbitrary line defined byslopeandintercept, computex * slope + intercept.
- To make a prediction for
- For this dataset, if we choose a different line, we will end up with different predictions, and hence a different RMSE.
def rmse(slope, intercept):
'''Calculates the RMSE of the line with the given slope and intercept,
using the 'x' and 'y' columns of without_outlier.'''
# The true values of y.
true = without_outlier.get('y')
# The predicted values of y, from plugging the x values from the
# given DataFrame into the line with the given slope and intercept.
predicted = slope * without_outlier.get('x') + intercept
return np.sqrt(((true - predicted) ** 2).mean())
# Check that our function works on the regression line.
rmse(m_no_outlier, b_no_outlier)
2.1963083164755415
Let's compute the RMSEs of several different lines on the same dataset.
# Experiment by changing one of these!
lines = [(1.2, -15), (0.75, 11.5), (-0.4, 100)]
fig, ax = plt.subplots(1, 3, figsize=(14, 4))
for i, line in enumerate(lines):
plt.subplot(1, 3, i + 1)
m, b = line
plot_errors(without_outlier, m, b, ax=ax[i])
ax[i].set_title(format_equation(m, b) + f'\nRMSE={np.round(rmse(m, b), 2)}')
Finding the "best" prediction line by minimizing RMSE¶
- RMSE describes how well a line fits the data. The lower the RMSE of a line is, the better it fits the data.
- There are infinitely many slopes and intercepts, and thus infinitely many RMSEs. How do we find which combination of slope and intercept have the lowest RMSE?
- If you take DSC 40A, you'll learn how to do this using calculus. For now, we'll use a Python function that can do it automatically –
minimize.
Aside: minimize¶
- The function
minimizetakes in a function as an argument, and returns the inputs to that function that produce the smallest output.
- For instance, we know that the minimizing input to the function $f(x) = (x - 5)^2 + 4$ is $x = 5$.
minimizecan find this, too:
def f(x):
return (x - 5) ** 2 + 4
# Plot of f(x).
x = np.linspace(0, 10)
y = f(x)
plt.plot(x, y)
plt.title(r'$f(x) = (x - 5)^2 + 4$');
minimize(f)
array([5.])
- The
minimizefunction uses calculus and intelligent trial-and-error to find these inputs; you don't need to know how it works under the hood.
Finding the "best" prediction line by minimizing RMSE¶
We'll use minimize on rmse, to find the slope and intercept of the line with the smallest RMSE.
smallest_rmse_line = minimize(rmse)
smallest_rmse_line
array([0.98, 3.04])
Do these numbers look familiar?
Coincidence?¶
# The slope and intercept with the smallest RMSE, from our call to minimize.
m_smallest_rmse = smallest_rmse_line[0]
b_smallest_rmse = smallest_rmse_line[1]
m_smallest_rmse, b_smallest_rmse
(0.9759274403306587, 3.0423564735104427)
# The slope and intercept according to our regression line formulas.
slope(without_outlier, 'x', 'y'), intercept(without_outlier, 'x', 'y')
(0.9759277157245881, 3.042337135297416)
The slopes and intercepts we got using both approaches look awfully similar... 👀
The regression line is the best line!¶
- It turns out that the regression line we defined before before minimizes the root mean squared error (RMSE) among all lines.
$$m = r \cdot \frac{\text{SD of } y}{\text{SD of }x}$$
$$b = \text{mean of } y - m \cdot \text{mean of } x$$
- It is the best line, regardless of what our data looks like!
- All equivalent names:
- Line of “best fit”.
- Least squares line.
- Regression line.
- The technique of finding the slope and intercept that have the lowest RMSE is called the method of least squares.
Quality of fit¶
- The regression line describes the "best linear fit" for a given dataset.
- The formulas for the slope and intercept work no matter what the shape of the data is.
- But the line is only meaningful if the relationship between $x$ and $y$ is roughly linear.
Example: Non-linear data¶
What's the regression line for this dataset?
np.random.seed(23)
x2 = bpd.DataFrame().assign(
x=np.arange(-6, 6.1, 0.5) + np.random.normal(size=25),
y=np.arange(-6, 6.1, 0.5)**2 + np.random.normal(size=25)
)
x2.plot(kind='scatter', x='x', y='y', s=100, figsize=(10, 5));
plot_regression_line(x2, 'x', 'y')
This line doesn't fit the data at all!
Residuals¶
- Any set of predictions has errors.
$$\text{error} = \text{actual } y - \text{predicted } y$$
- When using the regression line to make predictions, the errors are called residuals.
$$\text{residual} = \text{actual } y - \text{predicted } y \text{ by regression line}$$
- There is one residual corresponding to each data point $(x, y)$ in the dataset.
- You'll explore residuals further in Lab 7, and we'll discuss them again in the next lecture.
Summary, next time¶
Summary¶
- The regression line in original units is $\text{predicted } y = mx + b$, where
$$m = r \cdot \frac{\text{SD of } y}{\text{SD of }x}$$
$$b = \text{mean of } y - m \cdot \text{mean of } x$$
- This line is very sensitive to outliers.
- This line has the lowest root mean squared error (RMSE) of all possible lines.
- It is the "line of best fit".
Next time¶
- As we saw, the regression line is the best line to fit the data, but not all data is linear.
- How do we determine whether fitting a line even makes sense for our dataset?
- When we use regression, we're making predictions based on data in a sample. What if we had a different sample?