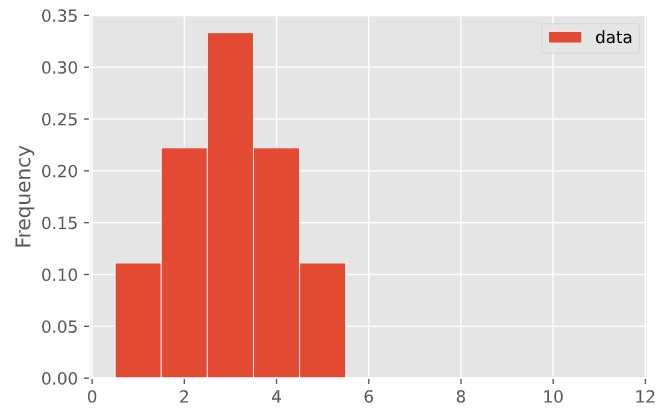
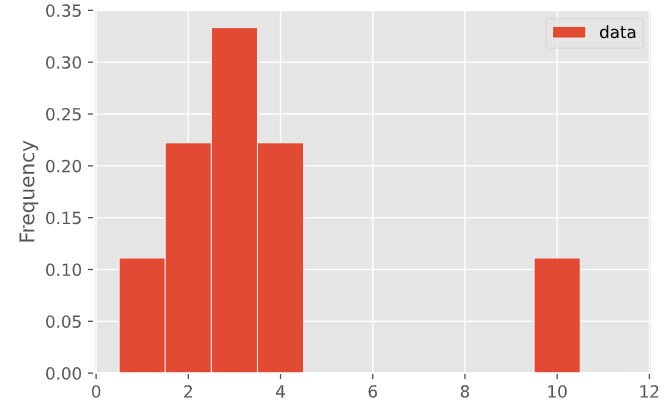
bpd.DataFrame().assign(BootstrapMedians=boot_medians).plot(kind='hist', density=True, bins=np.arange(63000, 88000, 1000), ec='w', figsize=(10, 5))
plt.plot([left, right], [0, 0], color='gold', linewidth=12, label='95% confidence interval');
plt.scatter(population_median, 0.000004, color='blue', s=100, label='population median').set_zorder(3)
plt.legend();