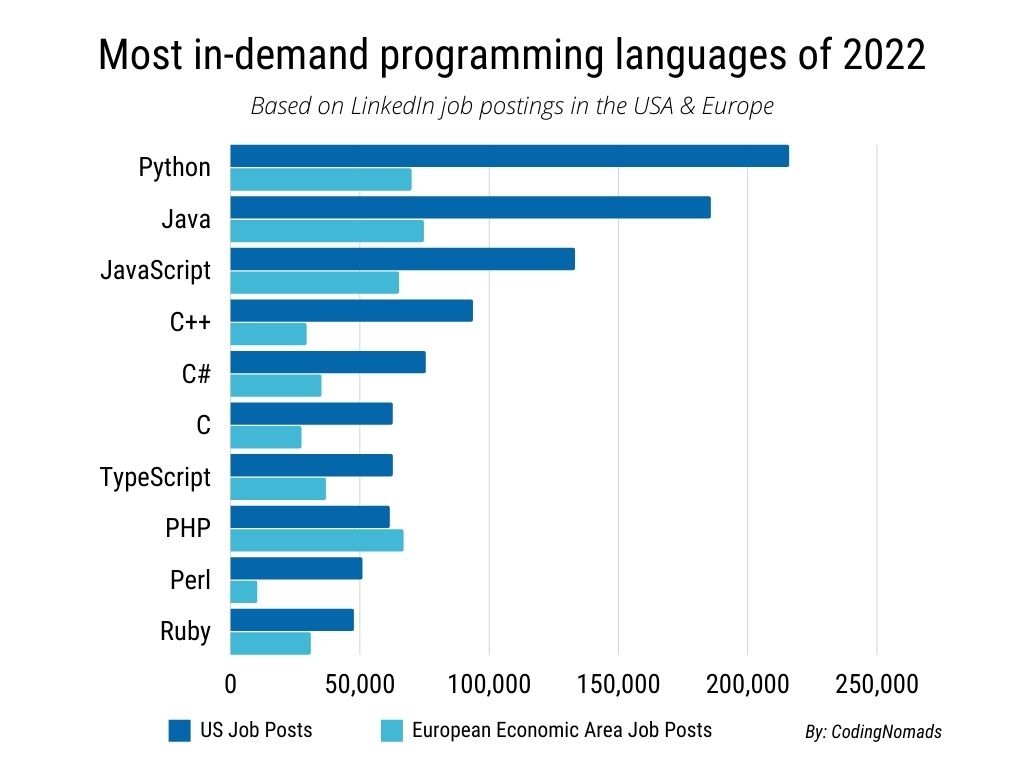
- It's popular!
# Don't worry about what this code does, but make sure to run it if you're following along.
from IPython.display import IFrame
def show_nested_eval():
src = 'https://docs.google.com/presentation/d/e/2PACX-1vQpW0NzwT3LjZsIIDAgtSMRM1cl41Gp_Lf8k9GT-gm5sGAIynw4rsgiEFbIybClD6QtxarKaVKLbR9U/embed?start=false&loop=false&delayms=60000&rm=minimal" frameborder="0" width="960" height="569" allowfullscreen="true" mozallowfullscreen="true" webkitallowfullscreen="true"'
width = 960
height = 569
return IFrame(src, width, height)
There will be lots of programming – follow along in the notebook by clicking the "Expressions and Data Types" link on the course website.

 This button!
This button!shift + enter (or shift + return) on your keyboard (strongly preferred), or23
23
-15 + 2.718
-12.282
4 ** 3
64
(2 + 3 + 4) / 3
3.0
# Only one value is displayed. Why?
9 + 10
13 / 4
21
21
| Operation | Operator | Example | Value |
|---|---|---|---|
| Addition | + |
2 + 3 |
5 |
| Subtraction | - |
2 - 3 |
-1 |
| Multiplication | * |
2 * 3 |
6 |
| Division | / |
7 / 3 |
2.66667 |
| Remainder | % |
7 % 3 |
1 |
| Exponentiation | ** |
2 ** 0.5 |
1.41421 |
5 * 2 ** 3
40
(5 * 2) ** 3
1000
In the cell below, replace the ellipses with an expression that's equivalent to
$$(19 + 6 \cdot 3) - 15 \cdot \left(\sqrt{100} \cdot \frac{1}{30}\right) \cdot \frac{3}{5} + \frac{4^2}{2^3} + \left( 6 - \frac{2}{3} \right) \cdot 12 $$Try to use parentheses only when necessary.
Below, we compute the number of seconds in a year.
60 * 60 * 24 * 365
31536000
If we want to use the above value later in our notebook to find, say, the number of seconds in 12 years, we'd have to copy-and-paste the expression. This is inconvenient, and prone to introducing errors.
60 * 60 * 24 * 365 * 12
378432000
It would be great if we could store the initial value and refer to it later on!
= symbol.= symbol is evaluated before being assigned to the name on the left-hand side.zebra is bound to 9 (value) not 23 - 14 (expression).# Note: This is an assignment statement, not an expression.
# Assignment statements don't output anything!
a = 1

a = 2

b = 2

Note that before we use it in an assignment statement, triton has no meaning.
triton
10
After using it in an assignment statement, we can ask Python for its value.
triton = 15 - 5
triton
10
Any time we use triton in an expression, 10 is substituted for it.
triton * -4
-40
Note that the above expression did not change the value of triton, because we did not re-assign triton!
triton
10
The following assignment statements are valid, but use poor variable names 😕.
six = 15
i_45love_chocolate_9999 = 60 * 60 * 24 * 365
The following assignment statements are valid, and use good variable names ✅.
seconds_per_hour = 60 * 60
hours_per_year = 24 * 365
seconds_per_year = seconds_per_hour * hours_per_year
The following "assignment statements" are invalid ❌.
7_days = 24 * 7
Cell In[92], line 1 7_days = 24 * 7 ^ SyntaxError: invalid decimal literal
3 = 2 + 1
Cell In[93], line 1 3 = 2 + 1 ^ SyntaxError: cannot assign to literal
= to the value to the right of =, nothing more.x = 3
3 = x
Cell In[95], line 1 3 = x ^ SyntaxError: cannot assign to literal
uc = 2
sd = 3 + uc
Assignment statements are not promises – the value of a variable can change!
uc = 7
Note that even after changing uc, we did not change sd, so it is still the same as before.
sd
5
Assume you have run the following three lines of code:
side_length = 5
area = side_length ** 2
side_length = side_length + 2
What are the values of side_length and area after execution?
A. side_length = 5, area = 25
B. side_length = 5, area = 49
C. side_length = 7, area = 25
D. side_length = 7, area = 49
E. None of the above
tab to autocomplete a set name¶
abs(-23)
23
max(4, -8)
4
max(2, -3, -6, 10, -4)
10
max(9)
--------------------------------------------------------------------------- TypeError Traceback (most recent call last) Cell In[102], line 1 ----> 1 max(9) TypeError: 'int' object is not iterable
# Only two arguments!
max(9 + 10, 9 - 10)
19
? after a function's name to see its documentation 📄¶Or use the help function, e.g. help(round).
round(1.45678)
1
round?
round(1.45678, 3)
1.457
We can nest many function calls to evaluate sophisticated expressions.
min(abs(max(-1, -2, -3, min(4, -2))), max(5, 100))
1
...how did that work?
show_nested_eval()
module.function(), called "dot notation".import math¶Some of the many functions built into the math module are sqrt, pow, and log.
import math
math.sqrt(16)
4.0
math.pow(2, 5)
32.0
# What base is log?
math.log?
# Tab completion for browsing.
math.
Cell In[113], line 2 math. ^ SyntaxError: invalid syntax
math also has constants built in!
math.pi
3.141592653589793
Assume you have run the following statements:
x = 3
y = -2
Which of these examples results in an error?
A. abs(x, y)
B. math.pow(x, abs(y))
C. round(x, max(abs(y ** 2)))
D. math.pow(x, math.pow(y, x))
E. More than one of the above
4 / 2
2.0
5 - 3
2
To us, 2.0 and 2 are the same number, $2$. But to Python, these appear to be different!
type function to check a value's type.int and float¶int: An integer of any size.float: A number with a decimal point.int¶+), subtract (-), multiply (*), or exponentiate (**) ints, the result will be another int.ints have arbitrary precision in Python, meaning that your calculations will always be exact. 7 - 15
-8
type(7 - 15)
int
2 ** 300
2037035976334486086268445688409378161051468393665936250636140449354381299763336706183397376
2 ** 3000
1230231922161117176931558813276752514640713895736833715766118029160058800614672948775360067838593459582429649254051804908512884180898236823585082482065348331234959350355845017413023320111360666922624728239756880416434478315693675013413090757208690376793296658810662941824493488451726505303712916005346747908623702673480919353936813105736620402352744776903840477883651100322409301983488363802930540482487909763484098253940728685132044408863734754271212592471778643949486688511721051561970432780747454823776808464180697103083861812184348565522740195796682622205511845512080552010310050255801589349645928001133745474220715013683413907542779063759833876101354235184245096670042160720629411581502371248008430447184842098610320580417992206662247328722122088513643683907670360209162653670641130936997002170500675501374723998766005827579300723253474890612250135171889174899079911291512399773872178519018229989376
float¶float is specified using a decimal point.float might be printed using scientific notation.3.2 + 2.5
5.7
type(3.2 + 2.5)
float
# The result is in scientific notation: e+90 means "times 10^90".
2.0 ** 300
2.037035976334486e+90
float¶floats have limited precision; after arithmetic, the final few decimal places can be wrong in unexpected ways.floats have limited size, though the limit is huge.1 + 0.2
1.2
1 + 0.1 + 0.1
1.2000000000000002
2.0 ** 3000
--------------------------------------------------------------------------- OverflowError Traceback (most recent call last) Cell In[126], line 1 ----> 1 2.0 ** 3000 OverflowError: (34, 'Result too large')
int and float¶ints and floats in an expression, the result will always be a float.ints, you get a float back.int and float functions.2.0 + 3
5.0
12 / 2
6.0
# Want an integer back.
int(12 / 2)
6
# int chops off the decimal point!
int(-2.9)
-2

Our notebook still remembers all of the variables we defined earlier in the lecture.
triton
10
ints and floats are numbers.ints are integers, while floats contain decimal points.Note: We will introduce some code in labs and homeworks as well. Not everything will be in lecture. You will learn by doing!