Lecture 3 – Strings, Lists, and Arrays¶

DSC 10, Winter 2024¶

Announcements¶

  • Lab 0 is due tomorrow at 11:59PM.
  • The solutions to the pretest are now posted. See how you did and watch the 🎥 video at the end to learn more about important test-taking skills.
  • Monday is a holiday so there is no lecture and no discussion.

Resources 🤝¶

  • We're covering a lot of content very quickly. If you're overwhelmed, just know that we're here to support you!
    • Ed and office hours are your friends!
  • Check the Resources tab of the course website for programming resources.

Agenda¶

  • Data types.
  • Strings. 🧶
  • Means and medians.
  • Lists.
  • Arrays.

Data types¶

int and float¶

  • Every value in Python has a type.
  • Use the type function to check a value's type.
  • There are two numeric data types:
    • int: An integer of any size.
    • float: A number with a decimal point.
In [1]:
# int.
6 + 4
Out[1]:
10
In [2]:
# float.
20 / 2
Out[2]:
10.0

Converting between int and float¶

  • If you mix ints and floats in an expression, the result will always be a float.
    • Note that when you divide two ints, you get a float back.
  • A value can be explicity coerced (i.e. converted) using the int and float functions.
In [3]:
2.0 + 3
Out[3]:
5.0
In [4]:
12 / 2
Out[4]:
6.0
In [5]:
# Want an integer back.
int(12 / 2)
Out[5]:
6
In [6]:
# int chops off the decimal point!
int(-2.9)
Out[6]:
-2

Strings 🧶¶

Strings 🧶¶

  • A string is a snippet of text of any length.
  • In Python, strings are enclosed by either single quotes or double quotes (doesn't matter which!)
In [7]:
'woof'
Out[7]:
'woof'
In [8]:
type('woof')
Out[8]:
str
In [9]:
"woof"
Out[9]:
'woof'
In [10]:
# A string, not an int!
"1998"
Out[10]:
'1998'

String arithmetic¶

When using the + symbol between two strings, the operation is called "concatenation".

In [11]:
s1 = 'baby'
s2 = '🐼'
In [12]:
s1 + s2
Out[12]:
'baby🐼'
In [13]:
s1 + ' ' + s2
Out[13]:
'baby 🐼'
In [14]:
s2 * 3
Out[14]:
'🐼🐼🐼'

String methods¶

  • Associated with strings are special functions, called string methods.
  • Access string methods with a . after the string ("dot notation").
    • For instance, to use the upper method on string s, we write s.upper().
  • Examples include upper, title, and replace, but there are many more.
In [15]:
my_cool_string = 'data science is super cool!'
In [16]:
my_cool_string.title()
Out[16]:
'Data Science Is Super Cool!'
In [17]:
my_cool_string.upper()
Out[17]:
'DATA SCIENCE IS SUPER COOL!'
In [18]:
my_cool_string.replace('super cool', '💯' * 3)
Out[18]:
'data science is 💯💯💯!'
In [19]:
# len is not a method, since it doesn't use dot notation.
len(my_cool_string)
Out[19]:
27

Type conversion to and from strings¶

  • Any value can be converted to a string using str.
  • Some strings can be converted to int and float.
In [20]:
str(3)
Out[20]:
'3'
In [21]:
float('3')
Out[21]:
3.0
In [22]:
int('4')
Out[22]:
4
In [ ]:
int('baby panda')
In [ ]:
int('4.3')

Concept Check ✅ – Answer at cc.dsc10.com¶

Assume you have run the following statements:

x = 3
y = '4'
z = '5.6'

Choose the expression that will be evaluated without an error.

A. x + y

B. x + int(y + z)

C. str(x) + int(y)

D. str(x) + z

E. All of them have errors

Means and medians¶

Describing numerical data¶

  • We now know how to store individual numbers (as ints or floats) and pieces of text (as strings). But we often we'll work with sequences, or ordered collections, of several data values.
  • For any collection of numbers, say temperatures, it can be helpful to summarize the data by its mean (i.e. average) or median.
  • Both mean and median are measures of central tendency – that is, they tell us roughly where the "center" of the data falls.

The mean (i.e. average)¶

The mean is a one-number summary of a collection of numbers.

For example, the mean of $1$, $4$, $7$, and $12$ is $\frac{1 + 4 + 7 + 12}{4} = 6$.

Observe that the mean:

  • Doesn't have to be equal to one of the data points.
  • Doesn't have to be an integer, even if all of the data points are integers.
  • Is somewhere between the min and max, but not necessarily halfway between.
  • Has the same units as the data.

The median¶

Like the mean, the median is a one-number summary of a collection of numbers.

  • To calculate it, sort the data points and pick the number in the middle.
    • If there are two middle numbers, we usually pick the number halfway between (i.e. the mean of the middle two).
  • Example:
    • $\text{Median}(1, 4, 7, 12, 32) = 7$
    • $\text{Median}(1, 4, 7, 12) = 5.5$

Mean vs. median¶

  • The mean and median of a dataset can be the same, but they don't need to be. They measure the center of a dataset in two different ways.
  • Two different datasets can have the same mean without having the same median, and vice versa.

Activity¶

  1. Find two different datasets that have the same mean and different medians.

  2. Find two different datasets that have the same median and different means.

  3. Find two different datasets that have the same median and the same mean.

Means and medians are just summaries; they don't tell the whole story about a dataset!

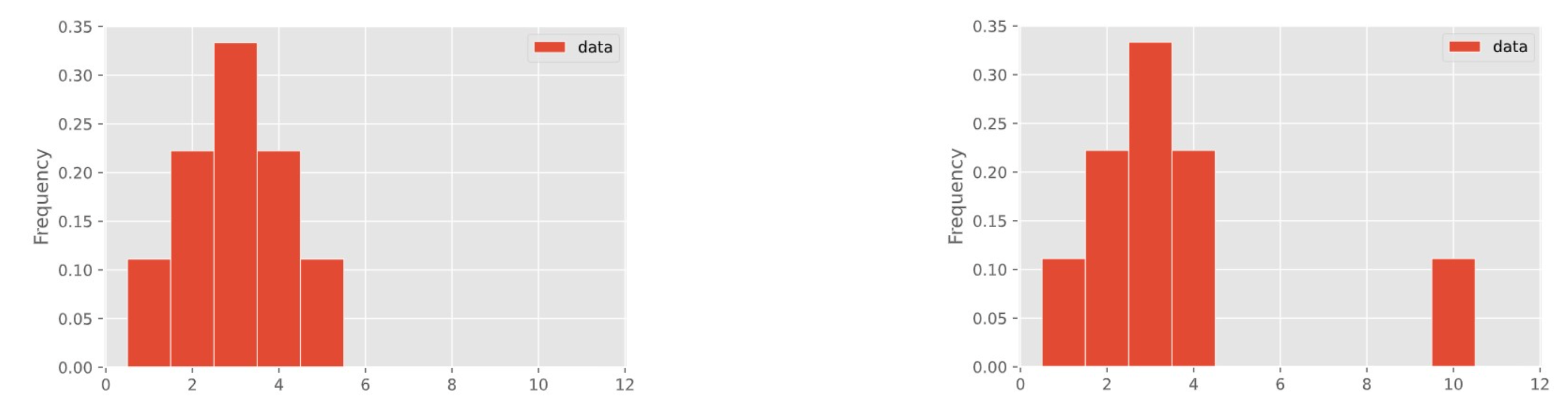
No description has been provided for this image

In a few weeks, we'll learn about how to visualize the distribution of a collection of numbers using a histogram.

These two distributions have different means but the same median!

Lists¶

Average temperature for a week¶

How would we store the temperatures for a week to compute the average temperature?

Our best solution right now is to create a separate variable for each day of the week.

In [25]:
temp_sunday = 68
temp_monday = 73
temp_tuesday = 70
temp_wednesday = 74
temp_thursday = 76
temp_friday = 72
temp_saturday = 74

This technically allows us to do things like compute the average temperature:

avg_temperature = 1/7 * (
    temp_sunday
    + temp_monday
    + temp_tuesday
    + ...)

Imagine a whole month's data, or a whole year's data. It seems like we need a better solution.

Lists in Python¶

In Python, a list is used to store multiple values within a single value. To create a new list from scratch, we use [square brackets].

In [26]:
temperature_list = [68, 73, 70, 74, 76, 72, 74]
In [27]:
len(temperature_list)
Out[27]:
7

Notice that the elements in a list don't need to be unique!

Lists make working with sequences easy!¶

To find the average temperature, we just need to divide the sum of the temperatures by the number of temperatures recorded:

In [28]:
temperature_list
Out[28]:
[68, 73, 70, 74, 76, 72, 74]
In [29]:
sum(temperature_list) / len(temperature_list)
Out[29]:
72.42857142857143

Types¶

The type of a list is... list.

In [30]:
temperature_list
Out[30]:
[68, 73, 70, 74, 76, 72, 74]
In [31]:
type(temperature_list)
Out[31]:
list

Within a list, you can store elements of different types.

In [32]:
mixed_list = [-2, 2.5, 'ucsd', [1, 3]]
mixed_list
Out[32]:
[-2, 2.5, 'ucsd', [1, 3]]

There's a problem...¶

  • Lists are very slow.
  • This is not a big deal when there aren't many entries, but it's a big problem when there are millions or billions of entries.

Arrays¶

NumPy¶

No description has been provided for this image

  • NumPy (pronounced "num pie") is a Python library (module) that provides support for arrays and operations on them.

  • The babypandas library, which you will learn about soon, goes hand-in-hand with NumPy.

    • NumPy is used heavily in the real world.

  • To use numpy, we need to import it. It's usually imported as np (but doesn't have to be!)

In [33]:
import numpy as np

Arrays¶

Think of NumPy arrays (just "arrays" from now on) as fancy, faster lists.

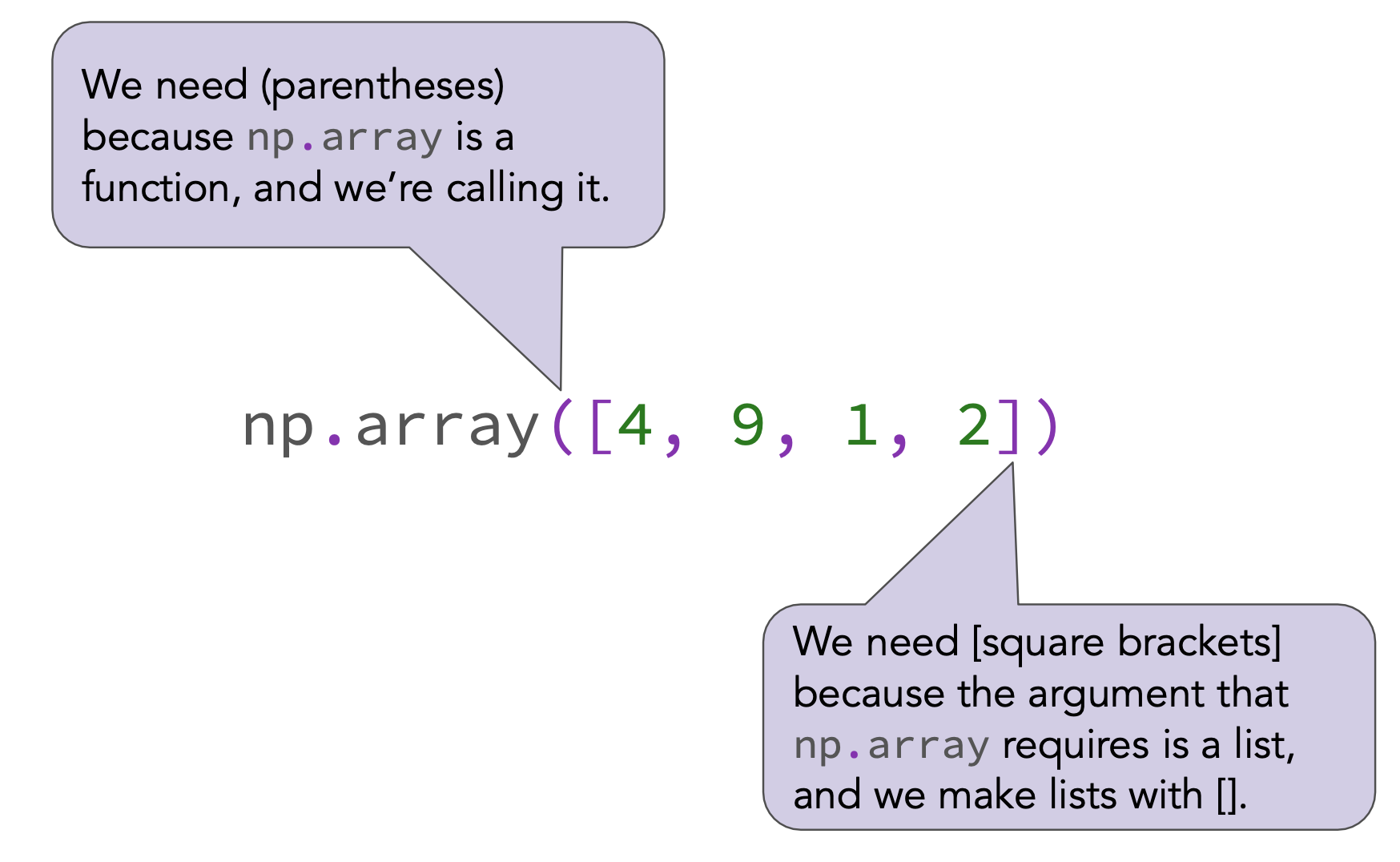
No description has been provided for this image

To create an array, we pass a list as input to the np.array function.

In [34]:
np.array([4, 9, 1, 2])
Out[34]:
array([4, 9, 1, 2])
No description has been provided for this image
In [35]:
temperature_array = np.array([68, 73, 70, 74, 76, 72, 74])
temperature_array
Out[35]:
array([68, 73, 70, 74, 76, 72, 74])
In [36]:
temperature_list
Out[36]:
[68, 73, 70, 74, 76, 72, 74]
In [37]:
# No square brackets, because temperature_list is already a list!
np.array(temperature_list)
Out[37]:
array([68, 73, 70, 74, 76, 72, 74])

Positions¶

When people wait in line, each person has a position.

No description has been provided for this image

Similarly, each element of an array (and list) has a position.

Accessing elements by position¶

  • Python, like most programming languages, is "0-indexed."
    • This means that the position of the first element in an array is 0, not 1.
    • One interpretation is that an element's position represents the number of elements in front of it.
  • To access the element in array arr_name at position pos, we use the syntax arr_name[pos].
In [38]:
temperature_array
Out[38]:
array([68, 73, 70, 74, 76, 72, 74])
In [39]:
temperature_array[0]
Out[39]:
68
In [40]:
temperature_array[1]
Out[40]:
73
In [41]:
temperature_array[3]
Out[41]:
74
In [42]:
# Access the last element.
temperature_array[6]
Out[42]:
74
In [ ]:
# Doesn't work!
temperature_array[7]
In [44]:
# If a position is negative, count from the end!
temperature_array[-1]
Out[44]:
74

Types¶

Earlier in the lecture, we saw that lists can store elements of multiple types.

In [45]:
nums_and_strings_lst = ['uc', 'sd', 1961, 3.14]
nums_and_strings_lst
Out[45]:
['uc', 'sd', 1961, 3.14]

This is not true of arrays – all elements in an array must be of the same type.

In [46]:
# All elements are converted to strings!
np.array(nums_and_strings_lst)
Out[46]:
array(['uc', 'sd', '1961', '3.14'], dtype='<U32')

Array-number arithmetic¶

Arrays make it easy to perform the same operation to every element. This behavior is formally known as "broadcasting".

No description has been provided for this image
In [47]:
temperature_array
Out[47]:
array([68, 73, 70, 74, 76, 72, 74])
In [48]:
# Increase all temperatures by 3 degrees.
temperature_array + 3
Out[48]:
array([71, 76, 73, 77, 79, 75, 77])
In [49]:
# Halve all temperatures.
temperature_array / 2
Out[49]:
array([34. , 36.5, 35. , 37. , 38. , 36. , 37. ])
In [50]:
# Convert all temperatures to Celsius.
(5 / 9) * (temperature_array - 32)
Out[50]:
array([20.        , 22.77777778, 21.11111111, 23.33333333, 24.44444444,
       22.22222222, 23.33333333])

Note: In none of the above cells did we actually modify temperature_array! Each of those expressions created a new array.

In [51]:
temperature_array
Out[51]:
array([68, 73, 70, 74, 76, 72, 74])

To actually change temperature_array, we need to reassign it to a new array.

In [52]:
temperature_array = (5 / 9) * (temperature_array - 32)
In [53]:
# Now in Celsius!
temperature_array
Out[53]:
array([20.        , 22.77777778, 21.11111111, 23.33333333, 24.44444444,
       22.22222222, 23.33333333])

Element-wise arithmetic¶

  • We can apply arithmetic operations to multiple arrays, provided they have the same length.
  • The result is computed element-wise, which means that the arithmetic operation is applied to one pair of elements from each array at a time.
No description has been provided for this image
In [54]:
a = np.array([4, 5, -1])
b = np.array([2, 3, 2])
In [55]:
a + b
Out[55]:
array([6, 8, 1])
In [56]:
a / b
Out[56]:
array([ 2.        ,  1.66666667, -0.5       ])
In [57]:
a ** 2 + b ** 2
Out[57]:
array([20, 34,  5])

Summary, next time¶

Summary¶

  • Strings are used to store text. Enclose them in single or double quotes.
  • Lists and arrays are used to store sequences.
    • Arrays are faster and more convenient for numerical operations.
    • Access elements by position, starting at position 0.
  • Remember to refer to the resources from the start of lecture!

Next time¶

We'll learn more about arrays and we'll see how to use Python to work with real-world tabular data.