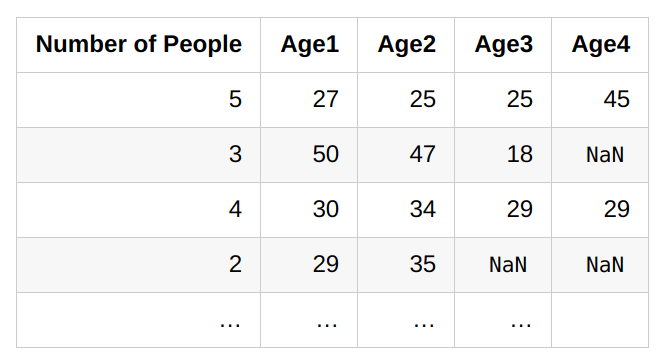
bins = np.linspace(-4, 4, 20)
plt.hist(differences, density=True, ec='w', bins=bins, alpha=0.65, label='Original Test Statistics');
plt.hist(faster_differences, density=True, ec='w', bins=bins, alpha=0.65, label='Faster Test Statistics')
plt.legend();