Lecture 22 – Modeling and sklearn

DSC 80, Spring 2022

Announcements

Agenda

Example: Restaurant tips 🧑‍🍳

Model #1: Constant

The first model we looked at last class used a constant tip amount prediction for every table.

$$\text{predicted tip} = h^*$$

If we use squared loss, the "best prediction is the mean of the observed tips.

Model #2: Tip percentages instead of tips

The next model we created used a constant tip percentage prediction for every table.

$$\text{predicted tip percentage} = h^*$$
$$\text{predicted tip} = \text{total bill} \cdot \text{mean pct-tip}$$

Constant tip vs. constant tip percentage

Model #3: Linear model

$$\text{predicted tip} = w_0^* + w_1^* \cdot \text{tip}$$

Fitting a linear model

We'll learn more about sklearn today.

Note that the above coefficients state that the "best way" (according to squared loss) to make tip predictions using a linear model is to assume people

Recap

What's next?

There's a lot of information in tips that we didn't use – 'sex', 'smoker', 'day', and 'time', for example. How might we encode this information?

One-hot encoding categorical variables

Let's one-hot encode the categorical columns in tips. Here's another way to do so manually:

Note that features has the same number of rows as tips; it just has more columns.

Let's fit a linear model using all features in features!

The RMSE of our latest model is the lowest of all linear models we've built so far (which is to be expected), but not by much. Perhaps these latest features weren't that useful.

We can visualize our latest model's predictions, too:

Why don't our model's predictions lie on a straight line? 🤔

Aside: Periodic sales

There is a pattern in the residual plot here, which is indicative that a linear model is not the best choice.

Example: Periodic sales

$$ \phi(x) = x + 5\sin\left(\frac{2\pi}{7} \cdot x\right) $$

Let's draw two scatter plots:

While neither the orange scatter plot nor the blue scatter plot look linear, the relationship between the $y$-values in the two scatter plots is roughly linear!

Our new linear model will use 'day_transformed' as the $x$ and 'units sold' as the $y$.

Now, the residual plot seems random, which is ideal!

sklearn overview

The steps of the modeling pipeline

  1. Create features to best reflect the "meaning" behind data.
  2. Choose a model that is appropriate to capture the relationships between features and the response.
  3. Select a loss function and fit the model (i.e., determine $w^*$).
  4. Evaluate the model (e.g. using RMSE).

Features and models using sklearn

preprocessing and linear_models

For the feature creation step of the modeling pipeline, we will use sklearn's preprocessing module.

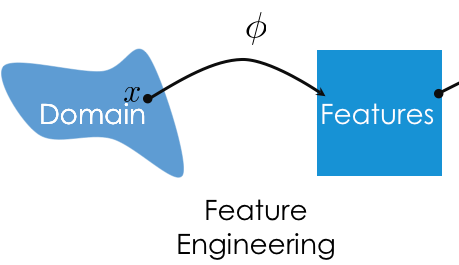
For the model creation step of the modeling pipeline, we will use sklearn's linear_model module.

Transformers in sklearn

Transformer classes

Example transformer: Binarizer

The Binarizer transformer allows us to map a quantitative sequence to a sequence of 1s and 0s, depending on whether values are above or below a threshold.

Property Example Description
Initialize with parameters binar = Binarizer(thresh) set x=1 if x > thresh, else 0
Transform data in a dataset feat = binar.transform(data) Binarize all columns in data

First, we need to import the relevant class from sklearn.preprocessing. (Tip: import just the relevant classes you need from sklearn.)

Let's try binarizing 'total_bill'. We'll say a "large" bill is one that is over \$20.

First, we initialize a Binarizer object with the threshold we want.

Then, we call bi's transform method and pass it the data we'd like to transform. Note that its input and output are both 2D.

Cool! We can verify that it worked correctly:

Example transformer: StdScaler

$$z_i = \frac{x_i - \bar{x}}{\sigma_x}$$
Property Example Description
Initialize with parameters stdscaler = StandardScaler() z-scale the data (no parameters)
Fit the transformer stdscaler.fit(data) compute the mean and SD of data
Transform data in a dataset feat = stdscaler.transform(newdata) z-scale newdata with mean and SD of data

It only makes sense to standardize the already-quantitative columns of tips, so let's select just those.

Let's initialize a StandardScaler object.

Note that the following does not work! The error message is very helpful.

Instead, we need to first call the fit method on stdscaler.

Now, transform will work.

We can also access the mean and variance stdscaler computed for each column:

Note that we can call transform on DataFrames other than tips_quant:

Example transformer: OneHotEncoder

Let's keep just the categorical columns in tips.

Like StdScaler, we will need to fit our OneHotEncoder transformer before it can transform anything.

We can look at the unique values (i.e. categories) in each column by using the categories_ attribute:

Since the resulting matrix is sparse – most of its elements are 0 – sklearn uses a more efficient representation than a regular numpy array. That's no issue, though:

Notice that the column names from tips_cat are no longer stored anywhere (remember, fit converts the input to a numpy array before proceeding).

We can use the get_feature_names method on ohe to access the names of the one-hot-encoded columns, though:

ohe also has an inverse_transform method, which takes a one-hot-encoded matrix and returns a categorical matrix.

Models in sklearn

Model classes

The LinearRegression class

We've seen this a few times in lecture already, but never formally.

Important: From the documentation, we have

LinearRegression fits a linear model with coefficients w = (w1, …, wp) to minimize the residual sum of squares between the observed targets in the dataset, and the targets predicted by the linear approximation.

In other words, LinearRegression minimizes mean squared error by default.

Additionally, by default the fit_intercept argument is set to True.

Example: Predicting 'tip' from 'total_bill' and 'size'

First, we instantiate and fit. By calling fit, we are saying "minimize mean squared error and find $w^*$".

After fitting, the predict method is available. Note that the argument to predict can be any 2D array with two columns.

We can access the intercepts and slopes individually. This model is of the form

$$\text{predicted tip} = w_0^* + w_1^* \cdot \text{total bill} + w_2^* \cdot \text{table size}$$

so we should expect three parameters total.

If we want to compute the RMSE of our model, we need to find its predictions on every row in the training data (tips).

It turns out that fit LinearRegression objects also have a score method:

That doesn't look like the RMSE... what is it? 🤔

Aside: $R^2$

$$R^2 = \frac{\text{var}(\text{predicted $y$ values})}{\text{var}(\text{actual $y$ values})}$$$$R^2 = \left[ \text{correlation}(\text{predicted $y$ values}, \text{actual $y$ values}) \right]^2$$

Calculating $R^2$

Recall, all_preds contains the predicted 'tip' for every data point in tips.

Method 1: $R^2 = \frac{\text{var}(\text{predicted $y$ values})}{\text{var}(\text{actual $y$ values})}$

Method 2: $R^2 = \left[ \text{correlation}(\text{predicted $y$ values}, \text{actual $y$ values}) \right]^2$

Note: By correlation here, we are referring to $r$.

Method 3: lr.score

All three methods provide the same result!

LinearRegression summary

Property Example Description
Initialize model parameters lr = LinearRegression() Create (empty) linear regression model
Fit the model to the data lr.fit(data, responses) Determines regression coefficients
Use model for prediction lr.predict(newdata) Use regression line make predictions
Evaluate the model lr.score(data, responses) Calculate the $R^2$ of the LR model
Access model attributes lr.coef_ Access the regression coefficients

Note: Once fit, estimators like LinearRegression are just transformers (predict <-> transform).

Summary, next time

Summary