import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

from sklearn.linear_model import LinearRegression

plt.style.use('seaborn-white')
plt.rc('figure', dpi=100, figsize=(7, 5))
plt.rc('font', size=12)

import warnings
warnings.simplefilter('ignore')

Lecture 23 – Pipelines and Evaluation

DSC 80, Spring 2022

For fun: read this article from CBS 8 San Diego 💰🚒🚔.

Last year, the city paid \$52.93 million in overtime to the fire department. San Diego Police Department received the second highest out of any other department with \\$36.6 million.

Announcements

• Discussion 7 is due for extra credit tomorrow at 11:59PM.
  • See this post for a clarification.
• Lab 8 is due on Monday, May 23rd at 11:59PM.
• Project 4 is due Thursday, May 26th at 11:59PM.
  • See this post for more public tests for Question 5.
• Lab 7 grades are released.
  • See this post for more details.

Agenda

• Models in sklearn.
• Pipelines.
• Model evaluation 🧪.

Models in sklearn

Example: Predicting 'tip' from 'total_bill' and 'size'

tips = sns.load_dataset('tips')
tips.head()

	total_bill	tip	sex	smoker	day	time	size
0	16.99	1.01	Female	No	Sun	Dinner	2
1	10.34	1.66	Male	No	Sun	Dinner	3
2	21.01	3.50	Male	No	Sun	Dinner	3
3	23.68	3.31	Male	No	Sun	Dinner	2
4	24.59	3.61	Female	No	Sun	Dinner	4

First, we instantiate and fit. By calling fit, we are saying "minimize mean squared error and find $w^*$".

lr = LinearRegression()

# Note that there are two arguments to fit – X and y!
# (It is not necessary to write X= and y=)
lr.fit(X=tips[['total_bill', 'size']], y=tips['tip'])

LinearRegression()

After fitting, the predict method is available. Note that the argument to predict can be any 2D array with two columns.

# Predicted tip from a table of 3 that spends $25 
lr.predict([[25, 3]])

array([3.56457154])

# Predicted tip from a table of 14 that spends $1000 – probably not accurate!
lr.predict([[1000, 14]])

array([96.07865069])

We can access the intercepts and slopes individually. This model is of the form

$$\text{predicted tip} = w_0^* + w_1^* \cdot \text{total bill} + w_2^* \cdot \text{table size}$$

so we should expect three parameters total.

lr.intercept_

0.6689447408125031

lr.coef_

array([0.09271334, 0.19259779])

If we want to compute the RMSE of our model, we need to find its predictions on every row in the training data (tips).

all_preds = lr.predict(tips[['total_bill', 'size']])

np.sqrt(np.mean((all_preds - tips['tip']) ** 2))

1.007256127114662

It turns out that fit LinearRegression objects also have a score method:

lr.score(tips[['total_bill', 'size']], tips['tip'])

0.46786930879612587

That doesn't look like the RMSE... what is it? 🤔

Aside: $R^2$

• $R^2$, or the coefficient of determination, is a measure of the quality of a linear fit.
• There are a few equivalent ways of computing it, assuming your model is linear and has an intercept term:

$$R^2 = \frac{\text{var}(\text{predicted $y$ values})}{\text{var}(\text{actual $y$ values})}$$$$R^2 = \left[ \text{correlation}(\text{predicted $y$ values}, \text{actual $y$ values}) \right]^2$$

• In the simple linear regression case, it is the square of the correlation coefficient, $r$.
• Key idea: $R^2$ ranges from 0 to 1. The closer it is to 1, the better the linear fit is.
  • $R^2$ has no units of measurement, unlike RMSE.
• Interpretation: $R^2$ is the proportion of variance in $y$ that the linear model explains.

Calculating $R^2$

Recall, all_preds contains the predicted 'tip' for every data point in tips.

tips.head()

	total_bill	tip	sex	smoker	day	time	size
0	16.99	1.01	Female	No	Sun	Dinner	2
1	10.34	1.66	Male	No	Sun	Dinner	3
2	21.01	3.50	Male	No	Sun	Dinner	3
3	23.68	3.31	Male	No	Sun	Dinner	2
4	24.59	3.61	Female	No	Sun	Dinner	4

all_preds[:5]

array([2.62933992, 2.20539403, 3.19464533, 3.24959215, 3.71915687])

Method 1: $R^2 = \frac{\text{var}(\text{predicted $y$ values})}{\text{var}(\text{actual $y$ values})}$

np.var(all_preds) / np.var(tips['tip'])

0.4678693087961252

Method 2: $R^2 = \left[ \text{correlation}(\text{predicted $y$ values}, \text{actual $y$ values}) \right]^2$

Note: By correlation here, we are referring to $r$.

(np.corrcoef(all_preds, tips['tip'])) ** 2

array([[1.        , 0.46786931],
       [0.46786931, 1.        ]])

Method 3: lr.score

lr.score(tips[['total_bill', 'size']], tips['tip'])

0.46786930879612587

All three methods provide the same result!

LinearRegression summary

Property	Example	Description
Initialize model parameters	lr = LinearRegression()	Create (empty) linear regression model
Fit the model to the data	lr.fit(data, responses)	Determines regression coefficients
Use model for prediction	lr.predict(newdata)	Use regression line make predictions
Evaluate the model	lr.score(data, responses)	Calculate the $R^2$ of the LR model
Access model attributes	lr.coef_	Access the regression coefficients

Note: Once fit, estimators like LinearRegression are just transformers (predict <-> transform).

Pipelines

So far, we've used transformers for feature engineering and models for prediction. We can combine these steps into a single Pipeline.

Pipelines in sklearn

• A Pipeline object is instantiated using a list containing transformer(s) and a model (estimator).

  pl = Pipeline([feat_trans1, feat_trans2, ..., mdl])
  

• Once a Pipeline is instantiated, you can fit all steps (transformers and model) using fit.

  pl.fit(data, responses)
  

• To make predictions using raw (untransformed) data, use pl.predict.

Creating a Pipeline

• To instantiate a Pipeline, we must provide a list with zero or more transformers followed by a single model.
  • All "steps" must have fit methods, and all but the last must have transform methods.
• The list we provide Pipeline with must be a list of tuples, where
  • The first element is a "name" (that we choose) for the step.
  • The second element is a transformer or estimator instance.

Let's build a Pipeline that:

• One-hot-encodes the categorical features in tips.
• Fits a regression model on the one-hot-encoded data.

tips_cat = tips[['sex', 'smoker', 'day', 'time']]
tips_cat.head()

	sex	smoker	day	time
0	Female	No	Sun	Dinner
1	Male	No	Sun	Dinner
2	Male	No	Sun	Dinner
3	Male	No	Sun	Dinner
4	Female	No	Sun	Dinner

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import OneHotEncoder

pl = Pipeline([
    ('one-hot', OneHotEncoder()),
    ('lin-reg', LinearRegression())
])

Now that pl is instantiated, we fit it the same way we would fit the individual steps.

pl.fit(tips_cat, tips['tip'])

Pipeline(steps=[('one-hot', OneHotEncoder()), ('lin-reg', LinearRegression())])

Now, to make predictions using raw data, all we need to do is use pl.predict:

pl.predict([['Male', 'Yes', 'Sat', 'Lunch']])

array([2.58813051])

pl.predict(tips_cat.iloc[:5])

array([3.10415414, 3.27436302, 3.27436302, 3.27436302, 3.10415414])

pl performs both feature transformation and prediction with just a single call to predict!

We can access individual "steps" of a Pipeline through the named_steps attribute:

pl.named_steps

{'one-hot': OneHotEncoder(), 'lin-reg': LinearRegression()}

pl.named_steps['one-hot'].transform(tips_cat).toarray()

array([[1., 0., 1., ..., 0., 1., 0.],
       [0., 1., 1., ..., 0., 1., 0.],
       [0., 1., 1., ..., 0., 1., 0.],
       ...,
       [0., 1., 0., ..., 0., 1., 0.],
       [0., 1., 1., ..., 0., 1., 0.],
       [1., 0., 1., ..., 1., 1., 0.]])

pl.named_steps['lin-reg'].coef_

array([-0.08510444,  0.08510444, -0.04216238,  0.04216238, -0.20256076,
       -0.12962763,  0.13756057,  0.19462781,  0.25168453, -0.25168453])

More sophisticated Pipelines

• In the previous example, we one-hot-encoded every input column. What if we want to perform different transformations on different columns?
• Solution: Use a ColumnTransformer.
  • Instantiate a ColumnTransformer using a list of tuples, where:
    • The first element is a "name" we choose for the transformer.
    • The second element is a transformer instance (e.g. OneHotEncoder()).
    • The third element is a list of relevant column names.
  • ColumnTransformer is extremely useful, but it was only added to sklearn in 2018!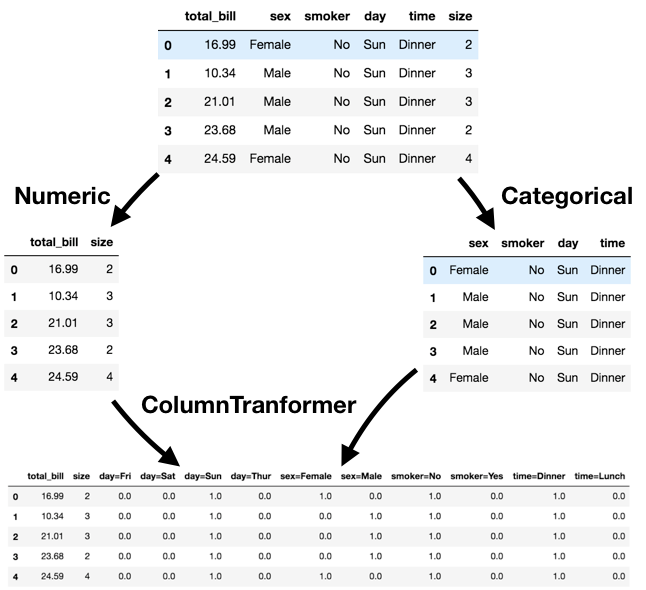

from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import StandardScaler

Let's perform different transformations on the quantitative and categorical features of tips (so, we will not transform 'tip').

tips_features = tips.drop('tip', axis=1)
tips_features.head()

	total_bill	sex	smoker	day	time	size
0	16.99	Female	No	Sun	Dinner	2
1	10.34	Male	No	Sun	Dinner	3
2	21.01	Male	No	Sun	Dinner	3
3	23.68	Male	No	Sun	Dinner	2
4	24.59	Female	No	Sun	Dinner	4

• To the quantitative features ('total_bill' and 'size'), we will apply the StandardScaler transformer.
• To the categorical features, we will apply the OneHotEncoder transformer.

preproc = ColumnTransformer(
    transformers = [
        ('quant', StandardScaler(), ['total_bill', 'size']),
        ('cat', OneHotEncoder(), ['sex', 'smoker', 'day', 'time'])
    ]
)

Now, let's create a Pipeline using preproc as a transformer, and fit it:

pl = Pipeline([
    ('preprocessor', preproc), 
    ('lin-reg', LinearRegression())
])

pl.fit(tips_features, tips['tip'])

Pipeline(steps=[('preprocessor',
                 ColumnTransformer(transformers=[('quant', StandardScaler(),
                                                  ['total_bill', 'size']),
                                                 ('cat', OneHotEncoder(),
                                                  ['sex', 'smoker', 'day',
                                                   'time'])])),
                ('lin-reg', LinearRegression())])

Prediction is as easy as calling predict:

tips_features.head()

	total_bill	sex	smoker	day	time	size
0	16.99	Female	No	Sun	Dinner	2
1	10.34	Male	No	Sun	Dinner	3
2	21.01	Male	No	Sun	Dinner	3
3	23.68	Male	No	Sun	Dinner	2
4	24.59	Female	No	Sun	Dinner	4

pl.predict(tips_features.head())

array([2.73565486, 2.25086733, 3.25904369, 3.33533199, 3.80574011])

pl also has a score method, the same way a fit LinearRegression instance does:

pl.score(tips_features, tips['tip'])

0.47007812322060794

Recall, we can access the individual "steps" in pl using the named_steps attribute:

pl.named_steps['preprocessor'].transform(tips_features)

array([[-0.31471131, -0.60019263,  1.        , ...,  0.        ,
         1.        ,  0.        ],
       [-1.06323531,  0.45338292,  0.        , ...,  0.        ,
         1.        ,  0.        ],
       [ 0.1377799 ,  0.45338292,  0.        , ...,  0.        ,
         1.        ,  0.        ],
       ...,
       [ 0.3246295 , -0.60019263,  0.        , ...,  0.        ,
         1.        ,  0.        ],
       [-0.2212865 , -0.60019263,  0.        , ...,  0.        ,
         1.        ,  0.        ],
       [-0.1132289 , -0.60019263,  1.        , ...,  1.        ,
         1.        ,  0.        ]])

Note: ColumnTransformer has a remainder argument that you can use to specify what to do with columns that aren't being transfromed ('drop' or 'passthrough').

Model evaluation 🧪

Motivation

• You and Billy are studying for an upcoming exam. You both decide to test your understanding by taking a practice exam.
  • Your logic: If you do well on the practice exam, you should do well on the real exam.

• You each take the practice exam once and look at the solutions afterwards.

• Your strategy: Memorize the answers to all practice exam questions, e.g. "Question 1: A; Question 2: C; Question 3: A."

• Billy's strategy: Learn high-level concepts from the solutions, e.g. "data are NMAR if the likelihood of missingness depends on the missing values themselves."

• Who will do better on the practice exam? Who will probably do better on the real exam? 🧐

Evaluating the quality of a model

• So far, we've computed the RMSE (and $R^2$) of our fit regression models on the data that we used to fit them, i.e. the training data.
• We've said that Model A is better than Model B if Model A's RMSE is lower than Model B's RMSE.
  • Remember, our training data is a sample from the data generating process.
  • Just because a model fits the training data well doesn't mean it will generalize and work well on similar, unseen samples!

Example: Overfitting and underfitting

Let's collect two samples $\{(x_i, y_i)\}$ from the same data generating process.

np.random.seed(23) # For reproducibility

def sample_dgp(n=100):
    x = np.linspace(-2, 3, n)
    y = x ** 3 + (np.random.normal(0, 3, size=n))
    return x.reshape(-1, 1), y

x1, y1 = sample_dgp()
x2, y2 = sample_dgp()

For now, let's just look at Sample 1. The relationship between $x$ and $y$ is roughly cubic; that is, $y \approx x^3$ (remember, in reality, you won't get to see the DGP).

plt.scatter(x1, y1);

Let's fit three polynomial models on Sample 1:

• Degree 1.
• Degree 3.
• Degree 15.

The PolynomialFeatures transformer will be helpful here.

from sklearn.preprocessing import PolynomialFeatures

d2 = PolynomialFeatures(3)
d2.fit_transform([[1], [2], [3], [4], [5]]) # fit_transform fits and transforms the same input

array([[  1.,   1.,   1.,   1.],
       [  1.,   2.,   4.,   8.],
       [  1.,   3.,   9.,  27.],
       [  1.,   4.,  16.,  64.],
       [  1.,   5.,  25., 125.]])

degs = [1, 3, 15]

def fit_polys(x, y):
    # Create all three Pipelines
    pls = [
        Pipeline([('poly', PolynomialFeatures(d)), ('lin-reg', LinearRegression())])
        for d in degs
    ]

    # Fit all three Pipelines
    [pl.fit(x, y) for pl in pls];

    # Make all three sets of predictions
    preds = [pl.predict(x) for pl in pls]
    return preds
    
preds_1 = fit_polys(x1, y1)

Below, we look at our three models' predictions on Sample 1 (which they were trained on).

plt.subplots(1, 3, figsize=(15, 5), dpi=100)
plt.suptitle('Performance on Sample 1\n')

for i in range(1, 4):
    plt.subplot(1, 3, i)
    plt.scatter(x1, y1, label='actual')
    plt.plot(x1, preds_1[i-1], color='orange', label='predictions', linewidth=5)
    rmse_d = np.sqrt(np.mean((preds_1[i-1] - y1) ** 2))
    plt.title(f'Degree {degs[i-1]}, RMSE: {np.round(rmse_d, 2)}')
plt.legend(loc=(1.04, 0))
plt.show()

The degree 15 polynomial has the lowest RMSE on Sample 1.

How do things look in Sample 2?

plt.subplots(1, 3, figsize=(15, 5), dpi=100)
plt.suptitle('Performance on Sample 2\n')

for i in range(1, 4):
    plt.subplot(1, 3, i)
    plt.scatter(x2, y2, label='actual')
    plt.plot(x1, preds_1[i-1], color='orange', label='predictions', linewidth=5)
    rmse_d = np.sqrt(np.mean((preds_1[i-1] - y2) ** 2))
    plt.title(f'Degree {degs[i-1]}, RMSE: {np.round(rmse_d, 2)}')
plt.legend(loc=(1.04, 0))
plt.show()

• The degree 3 polynomial has the lowest RMSE on Sample 2.
• Note that we didn't get to see Sample 2 when fitting our models!
• As such, it seems that the degree 3 polynomial generalizes better to unseen data than the degree 15 polynomial does.

What if we fit a degree 1, degree 3, and degree 15 polynomial on Sample 2 as well?

preds_2 = fit_polys(x2, y2)

plt.subplots(1, 3, figsize=(15, 5), dpi=100)
plt.suptitle('Models Fit on Samples 1 and 2\n')

for i in range(1, 4):
    plt.subplot(1, 3, i)
#     plt.scatter(x2, y2, label='actual')
    plt.plot(x1, preds_1[i-1], color='orange', label='Fit on Sample 1', linewidth=5)
    plt.plot(x2, preds_2[i-1], color='purple', label='Fit on Sample 2', linewidth=5)
    plt.title(f'Degree {degs[i-1]}')
plt.legend(loc=(1.04, 0))
plt.show()

Key idea: The degree 15 polynomial seems to vary more than the degree 3 and 1 polynomials do.

Bias and variance

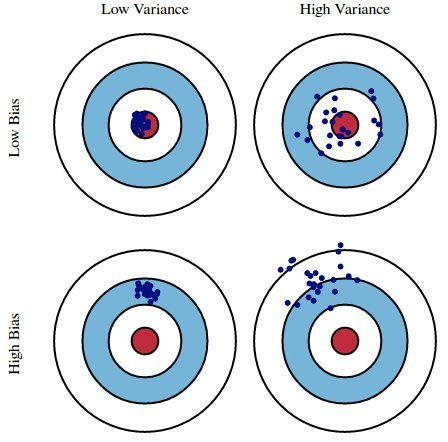
The training data we have access to is a sample from the DGP. We are concerned with our model's performance across different datasets from the same DGP.

Suppose we fit a model $H$ (e.g. a degree 3 polynomial) on several different datasets from a DGP. There are three sources of error that arise:

• ⭐️ Bias: The expected deviation between a predicted value and an actual value.
  • In other words, for a given $x_i$, how far is $H(x_i)$ from the true $y_i$, on average?
  • Low bias is good! ✅
  • High bias is a sign of underfitting, i.e. that our model is too basic to capture the relationship between our features and response.

• ⭐️ Model variance ("variance"): The variance of a model's predictions.
  • In other words, for a given $x_i$, what is the variance of $H(x_i)$ across all datasets?
  • Low model variance is good! ✅
  • High model variance is a sign of overfitting, i.e. that our model is too complicated and is prone to fitting to the noise in our training data.

• Observation variance: The variance due to the random noise in the process we are trying to model (e.g. measurement error). We can't control this, without collecting more data!

Here, suppose

• the red bulls-eye represents your true weight and height 🧍, and
• the blue darts represent predictions of your weight and height using different models that were fit on the same DGP.
  

Avoiding overfitting

• We won't know whether our model has overfit to our sample (training data) unless we get to see how well it performs on a new sample from the same DGP.

• Idea 💡: Split our sample into a training set and test set.

• Use only the training set to fit the model (i.e. find $w^*$).

• Use the test set to evaluate the model's error (RMSE, $R^2$).

• This is like "generating" new data from the same DGP!
  • Similar to bootstrapping (but not quite the same, because there is no resampling involved).
  • If our sample is not representative of the DGP, this method has limited effectiveness!

Train-test split 🚆

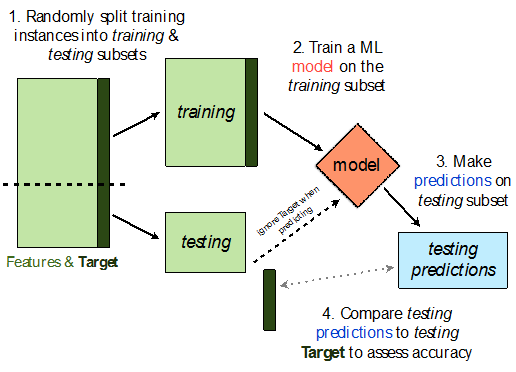
sklearn.model_selection.train_test_split implements a train-test split for us! 🙏🏼

If X is an array/DataFrame of features and y is an array/Series of responses,

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)

randomly splits the features and responses into training and test sets, such that the test set contains 0.25 of the full dataset.

from sklearn.model_selection import train_test_split

# Read the documentation!
train_test_split?

Let's perform a train/test split on our tips dataset.

X = tips.drop('tip', axis=1)
y = tips['tip']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) # Don't have to choose 0.25

Before proceeding, let's check the sizes of X_train and X_test.

print('Rows in X_train:', X_train.shape[0])
display(X_train.head())
print('Rows in X_test:', X_test.shape[0])
display(X_test.head())

Rows in X_train: 195

	total_bill	sex	smoker	day	time	size
4	24.59	Female	No	Sun	Dinner	4
209	12.76	Female	Yes	Sat	Dinner	2
178	9.60	Female	Yes	Sun	Dinner	2
230	24.01	Male	Yes	Sat	Dinner	4
5	25.29	Male	No	Sun	Dinner	4

Rows in X_test: 49

	total_bill	sex	smoker	day	time	size
146	18.64	Female	No	Thur	Lunch	3
224	13.42	Male	Yes	Fri	Lunch	2
134	18.26	Female	No	Thur	Lunch	2
131	20.27	Female	No	Thur	Lunch	2
147	11.87	Female	No	Thur	Lunch	2

X_train.shape[0] / tips.shape[0]

0.7991803278688525

Example prediction pipeline

Steps:

• Fit a model on the training set.
• Evaluate the model on the test set.

X = tips[['total_bill', 'size']] # For this example, we'll use just the already-quantitative columns in tips
y = tips['tip']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

Here, we'll use a stand-alone LinearRegression model without a Pipeline, but this process would work the same if we were using a Pipeline.

lr = LinearRegression()
lr.fit(X_train, y_train)

LinearRegression()

Let's check our model's performance on the training set first.

pred_train = lr.predict(X_train)
rmse_train = np.sqrt(np.mean((pred_train - y_train) ** 2))
rmse_train

1.0142193530579229

And the test set:

pred_test = lr.predict(X_test)
rmse_test = np.sqrt(np.mean((pred_test - y_test) ** 2))
rmse_test

0.983914318376069

Since rmse_train and rmse_test are similar, it doesn't seem like our model is overfitting to the training data. If rmse_test was much larger than rmse_train, it would be evidence that our model is unable to generalize well.

Summary, next time

Summary

• $R^2$ is a measure of a model's "goodness-of-fit". For linear models, it ranges between 0 (poor) and 1 (great).
• Pipelines in sklearn combine one or more transformers with a single model (estimator), allowing us to perform feature engineering and prediction through a single object.
• We want to build models that generalize well to unseen data.
  • Models that have high bias are too simple to represent complex relationships in data, and underfit.
  • Models that have high variance are overly complex for the relationships in the data, and vary a lot when fit on different datasets. Such models overfit to the training data.
• In order to prevent overfitting, we should perform a train-test split in which we only train our model on a subset of the data available to us, and use the remainder for evaluation.