Lecture 27 – Classifier Evaluation and Fairness

DSC 80, Spring 2022

Announcements

Agenda

Classifier evaluation

Recall

Predicted Negative Predicted Positive
Actually Negative TN = 90 ✅ FP = 1 ❌
Actually Positive FN = 8 ❌ TP = 1 ✅
UCSD Health test results

🤔 Question: What proportion of individuals who actually have COVID did the test identify?

🙋 Answer: $\frac{1}{1 + 8} = \frac{1}{9} \approx 0.11$

More generally, the recall of a binary classifier is the proportion of actually positive instances that are correctly classified. We'd like this number to be as close to 1 (100%) as possible.

$$\text{recall} = \frac{TP}{TP + FN}$$

To compute recall, look at the bottom (positive) row of the above confusion matrix.

Recall isn't everything, either!

$$\text{recall} = \frac{TP}{TP + FN}$$

🤔 Question: Can you design a "COVID test" with perfect recall?

🙋 Answer: Yes – just predict that everyone has COVID!

Predicted Negative Predicted Positive
Actually Negative TN = 0 ✅ FP = 91 ❌
Actually Positive FN = 0 ❌ TP = 9 ✅
everyone-has-COVID classifier
$$\text{recall} = \frac{TP}{TP + FN} = \frac{9}{9 + 0} = 1$$

Like accuracy, recall on its own is not a perfect metric. Even though the classifier we just created has perfect recall, it has 91 false positives!

Precision

Predicted Negative Predicted Positive
Actually Negative TN = 0 ✅ FP = 91 ❌
Actually Positive FN = 0 ❌ TP = 9 ✅
everyone-has-COVID classifier

The precision of a binary classifier is the proportion of predicted positive instances that are correctly classified. We'd like this number to be as close to 1 (100%) as possible.

$$\text{precision} = \frac{TP}{TP + FP}$$

To compute precision, look at the right (positive) column of the above confusion matrix.

Precision and recall

(source)

Precision and recall

$$\text{precision} = \frac{TP}{TP + FP} \: \: \: \: \: \: \: \: \text{recall} = \frac{TP}{TP + FN}$$

🤔 Question: When might high precision be more important than high recall?

🙋 Answer: For instance, in deciding whether or not someone committed a crime. Here, false positives are really bad – they mean that an innocent person is charged!

🤔 Question: When might high recall be more important than high precision?

🙋 Answer: For instance, in medical tests. Here, false negatives are really bad – they mean that someone's disease goes undetected!

Discussion Question

Consider the confusion matrix shown below.

Predicted Negative Predicted Positive
Actually Negative TN = 22 ✅ FP = 2 ❌
Actually Positive FN = 23 ❌ TP = 18 ✅

What is the accuracy of the above classifier? The precision? The recall?


After calculating all three on your own, click below to see the answers.

Accuracy (22 + 18) / (22 + 2 + 23 + 18) = 40 / 65
Precision 18 / (18 + 2) = 9 / 10
Recall 18 / (18 + 23) = 18 / 41

End of Final Exam content! 🎉

(Note that the remaining content is still relevant for Project 5.)

Example: Tumor malignancy prediction (via logistic regression)

Wisconsin breast cancer dataset

The Wisconsin breast cancer dataset (WBCD) is a commonly-used dataset for demonstrating binary classification. It is built into sklearn.datasets.

1 stands for "malignant", i.e. cancerous, and 0 stands for "benign", i.e. safe.

Our goal is to use the features in bc to predict labels.

Aside: Logistic regression

Logistic regression is a linear classification? technique that builds upon linear regression. It models the probability of belonging to class 1, given a feature vector:

$$P(y = 1 | \vec{x}) = \sigma (\underbrace{w_0 + w_1 x^{(1)} + w_2 x^{(2)} + ... + w_d x^{(d)}}_{\text{linear regression model}})$$

Here, $\sigma(t) = \frac{1}{1 + e^{-t}}$ is the sigmoid function; its outputs are between 0 and 1 (which means they can be interpreted as probabilities).

🤔 Question: Suppose our logistic regression model predicts the probability that a tumor is malignant is 0.75. What class do we predict – malignant or benign? What if the predicted probability is 0.3?

🙋 Answer: We have to pick a threshold (e.g. 0.5)!

Fitting a logistic regression model

How did clf come up with 1s and 0s?

It turns out that the predicted labels come from applying a threshold of 0.5 to the predicted probabilities. We can access the predicted probabilities via the predict_proba method:

Note that our model still has $w^*$s:

Evaluating our model

Let's see how well our model does on the test set.

Which metric is more important for this task – precision or recall?

What if we choose a different threshold?

🤔 Question: Suppose we choose a threshold higher than 0.5. What will happen to our model's precision and recall?

🙋 Answer: Precision will increase, while recall will decrease*.

Similarly, if we decrease our threshold, our model's precision will decrease, while its recall will increase.

Trying several thresholds

The classification threshold is not actually a hyperparameter of LogisticRegression, because the threshold doesn't change the coefficients ($w^*$s) of the logistic regression model itself (see this article for more details).

As such, if we want to imagine how our predicted classes would change with thresholds other than 0.5, we need to manually threshold.

Let's visualize the results in plotly, which is interactive.

The above curve is called a precision-recall (or PR) curve.

🤔 Question: Based on the PR curve above, what threshold would you choose?

Combining precision and recall

If we care equally about a model's precision $PR$ and recall $RE$, we can combine the two using a single metric called the F1-score:

$$\text{F1-score} = \text{harmonic mean}(PR, RE) = 2\frac{PR \cdot RE}{PR + RE}$$

Both F1-score and accuracy are overall measures of a binary classifier's performance. But remember, accuracy is misleading in the presence of class imbalance, and doesn't take into account the kinds of errors the classifier makes.

Other evaluation metrics for binary classifiers

We just scratched the surface! This excellent table from Wikipedia summarizes the many other metrics that exist.

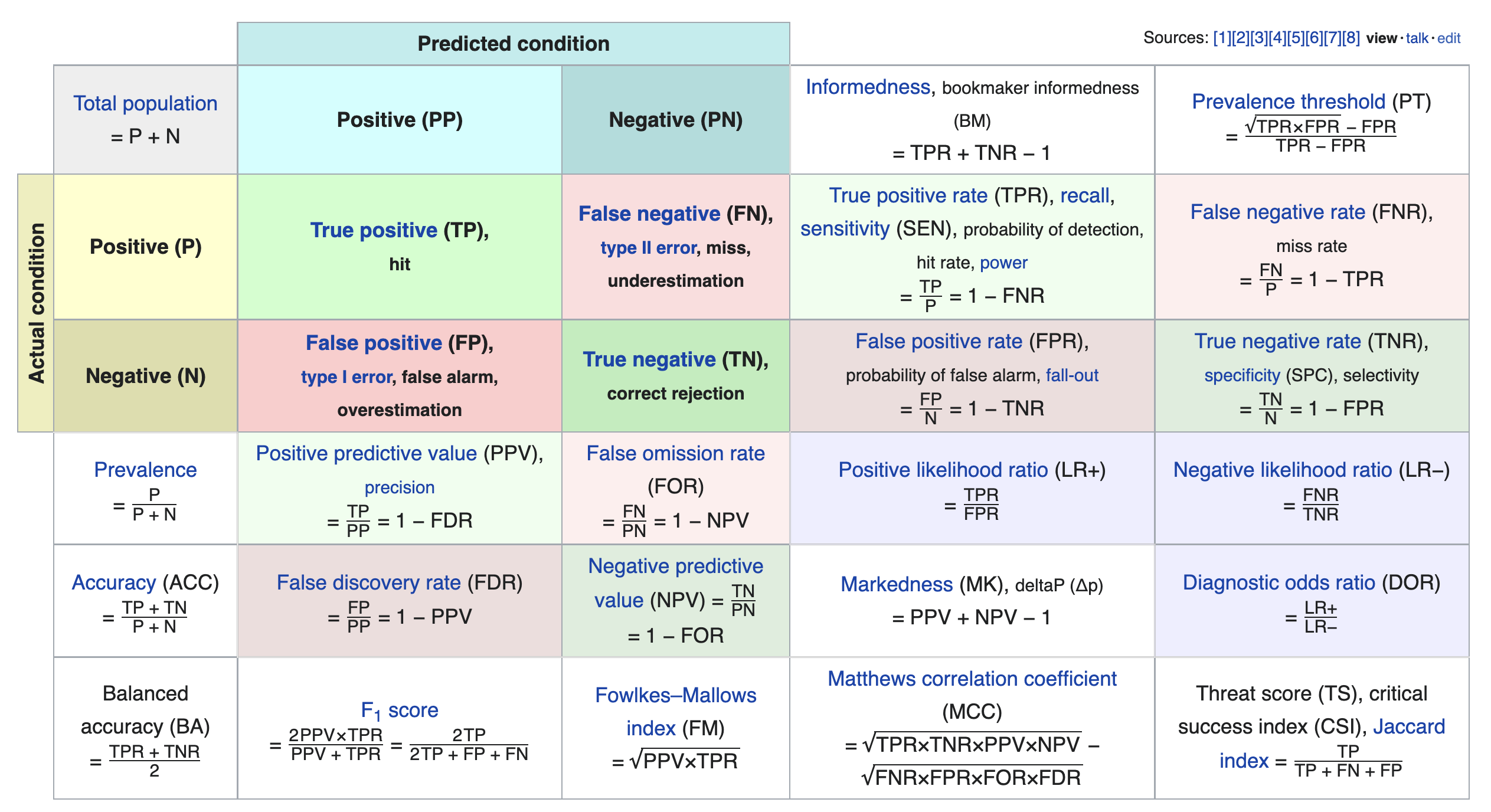
If you're interested in exploring further, a good next metric to look at is true negative rate (i.e. specificity), which is the analogue of recall for true negatives.

Fairness

Recall, from Lecture 1

Fairness: why do we care?

Example: COMPAS and recidivism prediction

COMPAS (Correctional Offender Management Profiling for Alternative Sanctions) is a "black-box" model that estimates the likelihood that someone who has commited a crime will recidivate (commit another crime).


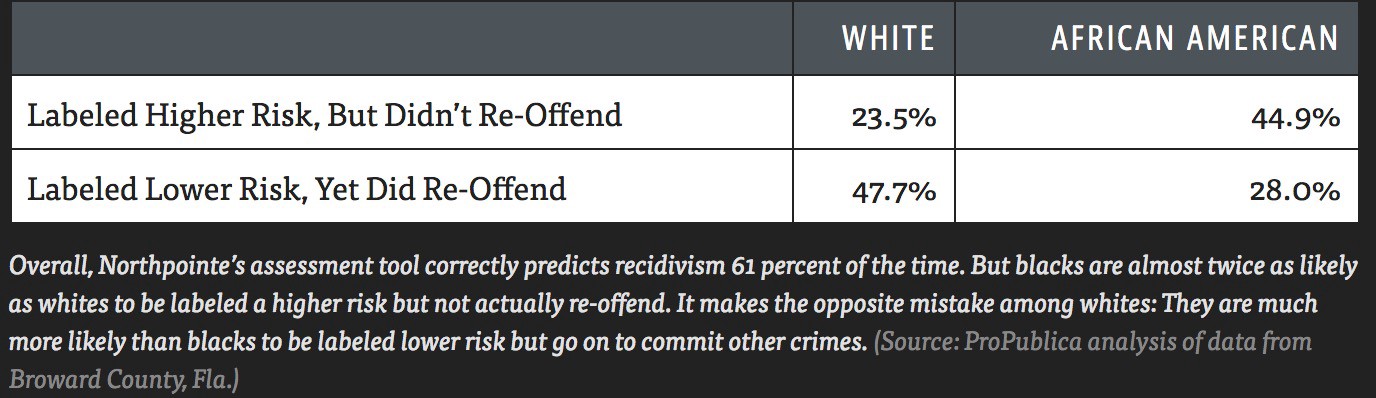
Propublica found that the model's false positive rate is higher for African-Americans than it is for White Americans, and that its false negative rate is lower for African-Americans than it is for White Americans.

Example: Facial recognition

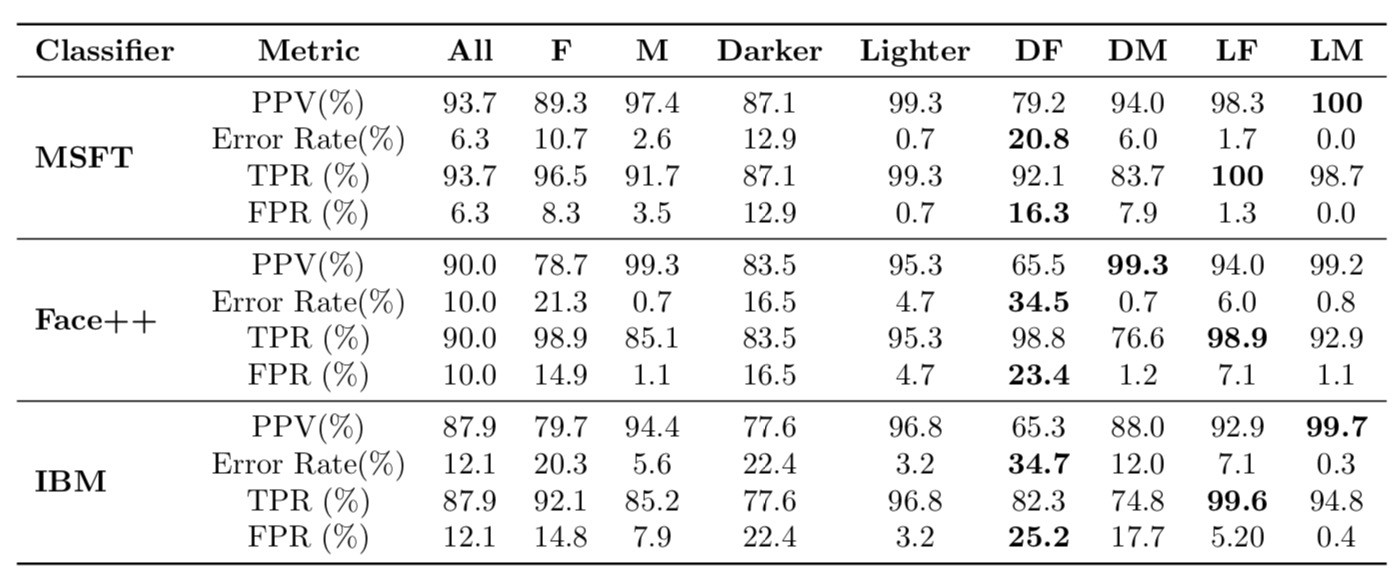
Note:

$$PPV = \text{precision} = \frac{TP}{TP+FP},\:\:\:\:\:\: TPR = \text{recall} = \frac{TP}{TP + FN}, \:\:\:\:\:\: FPR = \frac{FP}{FP+TN}$$

How does bias occur?

Remember, our models learn patterns from the training data. Various sources of bias may be present within training data:

Example: Gender associations

soldier, teacher, nurse, doctor, dog, cat, president, nanny

Example: Gender associations

Example: Image searches

A 2015 study examined the image queries of vocations and the gender makeup in the search results. Since 2015, the behavior of Google Images has been improved.

In 2015, a Google Images search for "nurse" returned...

Search for "nurse" now, what do you see?

In 2015, a Google Images search for "doctor" returned...

Search for "doctor" now, what do you see?

Ethics: What gender ratio should we expect in the results?

Excerpts:

"male-dominated professions tend to have even more men in their results than would be expected if the proportions reflected real-world distributions.

"People’s existing perceptions of gender ratios in occupations are quite accurate, but that manipulated search results have an effect on perceptions."

How did this unequal representation occur?

Summary, next time

Summary