In [1]:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib_inline.backend_inline import set_matplotlib_formats
from IPython.display import display, IFrame

# Pandas Tutor setup
%reload_ext pandas_tutor
%set_pandas_tutor_options {"maxDisplayCols": 8, "nohover": True, "projectorMode": True}

set_matplotlib_formats("svg")
sns.set_context("poster")
sns.set_style("whitegrid")
plt.rcParams["figure.figsize"] = (10, 5)
pd.set_option("display.max_rows", 8)
pd.set_option("display.max_columns", 8)
pd.set_option("display.precision", 2)

def show_paradox_slides():
    src = 'https://docs.google.com/presentation/d/e/2PACX-1vSbFSaxaYZ0NcgrgqZLvjhkjX-5MQzAITWAsEFZHnix3j1c0qN8Vd1rogTAQP7F7Nf5r-JWExnGey7h/embed?start=false'
    width = 960
    height = 569
    display(IFrame(src, width, height))

Lecture 3 – Aggregating, Simpson's paradox¶

DSC 80, Fall 2023¶

Agenda¶

  • Data granularity.
  • Grouping using .groupby() and .resample().
  • Pivot tables using .pivot_table().
  • Conditional probabilities
  • Simpson's paradox

📣 Announcements 📣¶

  • Good job turning in Lab 1!
  • Lab 2 out, due Monday.
  • Project 1 checkpoint due tomorrow.
    • Project 1 due next Wed.

Data granularity¶

Granularity¶

  • Granularity refers to what each observation in a dataset represents.
    • Fine: small details.
    • Coarse: bigger picture.
  • Most commonly, rows in a DataFrame correspond to observations, and columns correspond to attributes. Data formatted in this way is called tidy data.

Example: Baby Names¶

What is a single observation in the baby names data?

In [2]:
baby = pd.read_csv('data/baby.csv')
baby
Out[2]:
Name Sex Count Year
0 Liam M 20456 2022
1 Noah M 18621 2022
2 Olivia F 16573 2022
3 Oliver M 15076 2022
... ... ... ... ...
2085154 Worthy M 5 1880
2085155 Wright M 5 1880
2085156 York M 5 1880
2085157 Zachariah M 5 1880

2085158 rows × 4 columns

Example: CO2 readings¶

What is a single observation in this dataset of CO2 readings?

In [3]:
# Don't about this code, we'll cover it when we talk about data cleaning
co2 = pd.read_csv('data/co2_mm_mlo.txt', 
                  header=None, skiprows=72, sep='\s+',
                  names=['Yr', 'Mo', 'DecDate', 'Avg', 'co2', 'Trend', 'days'],
                  usecols=['Yr', 'Mo', 'DecDate', 'co2'])
co2
Out[3]:
Yr Mo DecDate co2
0 1958 3 1958.21 315.71
1 1958 4 1958.29 317.45
2 1958 5 1958.38 317.50
3 1958 6 1958.46 317.10
... ... ... ... ...
734 2019 5 2019.38 414.66
735 2019 6 2019.46 413.92
736 2019 7 2019.54 411.77
737 2019 8 2019.62 409.95

738 rows × 4 columns

Example: CO2 readings by month¶

In [4]:
# Don't worry about understanding this code for now
sns.lineplot(data=co2, x='DecDate', y='co2');
No description has been provided for this image

Collecting data¶

  • If you can control how your dataset is created, you should opt for finer granularity, i.e. for more detail.
  • You can easily remove detail, but it's difficult to add detail if it is not already present in the dataset.
  • Tradeoff: obtaining fine-grained data can take more time/money.

Manipulating granularity¶

  • We'll now explore how to change the level of granularity present in our dataset.
    • While it may seem like we are "losing information," removing detail can help us understand bigger-picture trends in our data.

Example: Penguins¶

No description has been provided for this image Artwork by @allison_horst

The dataset we'll work with for the rest of the lecture involves various measurements taken of three species of penguins in Antarctica.

In [5]:
import seaborn as sns
penguins = sns.load_dataset('penguins').dropna()
penguins
Out[5]:
species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g sex
0 Adelie Torgersen 39.1 18.7 181.0 3750.0 Male
1 Adelie Torgersen 39.5 17.4 186.0 3800.0 Female
2 Adelie Torgersen 40.3 18.0 195.0 3250.0 Female
4 Adelie Torgersen 36.7 19.3 193.0 3450.0 Female
... ... ... ... ... ... ... ...
340 Gentoo Biscoe 46.8 14.3 215.0 4850.0 Female
341 Gentoo Biscoe 50.4 15.7 222.0 5750.0 Male
342 Gentoo Biscoe 45.2 14.8 212.0 5200.0 Female
343 Gentoo Biscoe 49.9 16.1 213.0 5400.0 Male

333 rows × 7 columns

In [6]:
# What is the distribution of different 'species' in this dataset?
penguins['species'].value_counts()
Out[6]:
Adelie       146
Gentoo       119
Chinstrap     68
Name: species, dtype: int64
In [7]:
# Overall, what is the distribution of different islands?
penguins['island'].value_counts()
Out[7]:
Biscoe       163
Dream        123
Torgersen     47
Name: island, dtype: int64

Video: Palmer Penguins¶

In [8]:
IFrame('https://www.youtube-nocookie.com/embed/CCrNAHXUstU?si=-DntSyUNp5Kwitjm&start=11',
       width=560, height=315)
Out[8]:

Aggregating: Basics¶

We know how to find the mean body mass for all the penguins:

In [9]:
penguins['body_mass_g'].mean()
Out[9]:
4207.057057057057

💡 Pro-Tip: Using f-strings¶

Python f-strings give an easy way to print variables nicely:

In [10]:
mean_body_mass = penguins['body_mass_g'].mean()
print(f'Mean penguin mass: {mean_body_mass:.2f} grams')

Mean penguin mass: 4207.06 grams

Aggregating: Basics¶

But what about the mean for each type of penguin?

In [11]:
penguins['body_mass_g'].mean()
Out[11]:
4207.057057057057

Naive approach: looping through unique values¶

In [12]:
species_map = pd.Series([], dtype=float)

for species in penguins['species'].unique():
    species_only = penguins.loc[penguins['species'] == species]
    species_map.loc[species] = species_only['body_mass_g'].mean()
    
species_map
Out[12]:
Adelie       3706.16
Chinstrap    3733.09
Gentoo       5092.44
dtype: float64

  • For each unique 'species', we make a pass through the entire dataset.

    • The asymptotic runtime of this procedure is $\Theta(ns)$, where $n$ is the number of rows and $s$ is the number of unique species.

  • While there are other loop-based solutions that only involve a single pass over the DataFrame, we'd like to avoid Python loops entirely, as they're slow.

Grouping¶

In [13]:
# Before:
penguins['body_mass_g'].mean()

# After:
penguins.groupby('species')['body_mass_g'].mean()
Out[13]:
species
Adelie       3706.16
Chinstrap    3733.09
Gentoo       5092.44
Name: body_mass_g, dtype: float64

Somehow, the groupby method computes what we're looking for in just one line. How?

In [14]:
%%pt

penguins.groupby('species')['body_mass_g'].mean()

"Split-apply-combine" paradigm¶

The groupby method involves three steps: split, apply, and combine. This is the same terminology that the pandas documentation uses.

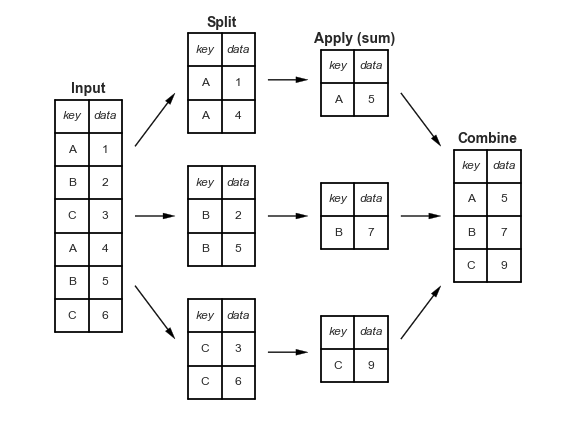
No description has been provided for this image

  • Split breaks up and "groups" the rows of a DataFrame according to the specified key. There is one "group" for every unique value of the key.

  • Apply uses a function (e.g. aggregation, transformation, filtration) within the individual groups.

  • Combine stitches the results of these operations into an output DataFrame.

  • The split-apply-combine pattern can be parallelized to work on multiple computers or threads, by sending computations for each group to different processors.

More examples¶

Before we dive into the internals, let's look at a few more examples.

In [15]:
penguins.head()
Out[15]:
species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g sex
0 Adelie Torgersen 39.1 18.7 181.0 3750.0 Male
1 Adelie Torgersen 39.5 17.4 186.0 3800.0 Female
2 Adelie Torgersen 40.3 18.0 195.0 3250.0 Female
4 Adelie Torgersen 36.7 19.3 193.0 3450.0 Female
5 Adelie Torgersen 39.3 20.6 190.0 3650.0 Male
In [16]:
penguins.shape
Out[16]:
(333, 7)

Which 'species' has the highest median 'bill_length_mm'?

In [17]:
(penguins
 .groupby('species')
 .median()
 ['bill_length_mm']
 .idxmax()
)
Out[17]:
'Chinstrap'

What proportion of penguins of each 'species' live on 'Dream' island?

In [18]:
(penguins
 .assign(on_dream = penguins['island'] == 'Dream')
 .groupby('species')
 .mean()['on_dream']
)
Out[18]:
species
Adelie       0.38
Chinstrap    1.00
Gentoo       0.00
Name: on_dream, dtype: float64

DataFrameGroupBy objects and aggregation¶

DataFrameGroupBy objects¶

We've just evaluated a few expressions of the following form.

In [19]:
penguins.groupby('species').mean()
Out[19]:
bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
species
Adelie 38.82 18.35 190.10 3706.16
Chinstrap 48.83 18.42 195.82 3733.09
Gentoo 47.57 15.00 217.24 5092.44

There are two method calls in the expression above: .groupby('species') and .mean(). What happens if we remove the latter?

In [20]:
penguins.groupby('species')
Out[20]:
<pandas.core.groupby.generic.DataFrameGroupBy object at 0x7fb8c011e070>

Peeking under the hood¶

If df is a DataFrame, then df.groupby(key) returns a DataFrameGroupBy object.

This object represents the "split" in "split-apply-combine".

In [21]:
# Simplified table for demostration:
penguins_small = penguins.iloc[[0, 1, 150, 151, 251, 300, 301], [0, 5, 6]]

# Creates one group for each unique value in the species column.
penguin_groups = penguins_small.groupby('species')
penguin_groups
Out[21]:
<pandas.core.groupby.generic.DataFrameGroupBy object at 0x7fb8c00ed640>
In [22]:
%%pt
penguin_groups

DataFrameGroupBy objects have a groups attribute, which is a dictionary in which the keys are group names and the values are lists of row labels.

In [23]:
penguin_groups.groups
Out[23]:
{'Adelie': [0, 1], 'Chinstrap': [156, 157], 'Gentoo': [258, 308, 309]}

DataFrameGroupBy objects also have a get_group(key) method, which returns a DataFrame with only the values for the given key.

In [24]:
penguin_groups.get_group('Chinstrap')
Out[24]:
species body_mass_g sex
156 Chinstrap 3725.0 Male
157 Chinstrap 3950.0 Female
In [25]:
# Same as the above!
penguins_small.query('species == "Chinstrap"')
Out[25]:
species body_mass_g sex
156 Chinstrap 3725.0 Male
157 Chinstrap 3950.0 Female

We usually don't use these attributes and methods, but they're useful in understanding how groupby works under the hood.

Aggregation¶

  • Once we create a DataFrameGroupBy object, we need to apply some function to each group, and combine the results.

  • The most common operation we apply to each group is an aggregation.

    • Aggregation refers to the process of reducing many values to one.

  • To perform an aggregation, use an aggregation method on the DataFrameGroupBy object, e.g. .mean(), .max(), or .median().

Let's look at some examples.

In [26]:
penguins_small
Out[26]:
species body_mass_g sex
0 Adelie 3750.0 Male
1 Adelie 3800.0 Female
156 Chinstrap 3725.0 Male
157 Chinstrap 3950.0 Female
258 Gentoo 4350.0 Female
308 Gentoo 4875.0 Female
309 Gentoo 5550.0 Male
In [27]:
penguins_small.groupby('species').mean()
Out[27]:
body_mass_g
species
Adelie 3775.0
Chinstrap 3837.5
Gentoo 4925.0
In [28]:
penguins_small.groupby('species').sum()
Out[28]:
body_mass_g
species
Adelie 7550.0
Chinstrap 7675.0
Gentoo 14775.0
In [29]:
penguins_small.groupby('species').last()
Out[29]:
body_mass_g sex
species
Adelie 3800.0 Female
Chinstrap 3950.0 Female
Gentoo 5550.0 Male
In [30]:
penguins_small.groupby('species').max()
Out[30]:
body_mass_g sex
species
Adelie 3800.0 Male
Chinstrap 3950.0 Male
Gentoo 5550.0 Male

Column independence¶

Within each group, the aggregation method is applied to each column independently.

In [31]:
penguins_small.groupby('species').max()
Out[31]:
body_mass_g sex
species
Adelie 3800.0 Male
Chinstrap 3950.0 Male
Gentoo 5550.0 Male

It is not telling us that there is a male 'Adelie' penguin with a 'body_mass_g' of 3800.0!

In [32]:
# This penguin is Female!
penguins_small.loc[(penguins['species'] == 'Adelie') & (penguins['body_mass_g'] == 3800.0)]
Out[32]:
species body_mass_g sex
1 Adelie 3800.0 Female

Discussion Question¶

Find the species and weights of the heaviest Male and Female penguins.

In [33]:
# Fill in this cell

Column selection and performance implications¶

  • By default, the aggregator will be applied to all columns that it can be applied to.

    • max and min are defined on strings, while median and mean are not.

  • If we only care about one column, we can select that column before aggregating to save time.

    • DataFrameGroupBy objects support [] notation, just like DataFrames.
In [34]:
# Back to the big penguins dataset
penguins.groupby('species').mean()
Out[34]:
bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
species
Adelie 38.82 18.35 190.10 3706.16
Chinstrap 48.83 18.42 195.82 3733.09
Gentoo 47.57 15.00 217.24 5092.44
In [35]:
# Works, but involves wasted effort since the other columns had to be aggregated for no reason.
penguins.groupby('species').mean()['bill_length_mm']
Out[35]:
species
Adelie       38.82
Chinstrap    48.83
Gentoo       47.57
Name: bill_length_mm, dtype: float64
In [36]:
# This is a SeriesGroupBy object!
penguins.groupby('species')['bill_length_mm']
Out[36]:
<pandas.core.groupby.generic.SeriesGroupBy object at 0x7fb8d46c14f0>
In [37]:
# Saves time!
penguins.groupby('species')['bill_length_mm'].mean()
Out[37]:
species
Adelie       38.82
Chinstrap    48.83
Gentoo       47.57
Name: bill_length_mm, dtype: float64

To demonstrate that the former is slower than the latter, we can use %%timeit. For reference, we'll also include our earlier for-loop-based solution.

In [38]:
%%timeit
penguins.groupby('species').mean()['bill_length_mm']

359 µs ± 1.94 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
In [39]:
%%timeit
penguins.groupby('species')['bill_length_mm'].mean()

137 µs ± 659 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
In [40]:
%%timeit
species_map = pd.Series([], dtype=float)

for species in penguins['species'].unique():
    species_only = penguins.loc[penguins['species'] == species]
    species_map.loc[species] = species_only['body_mass_g'].mean()
    
species_map

981 µs ± 1.88 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

Takeaways¶

  • It's important to understand what each piece of your code evaluates to – in the first two timed examples, the code is almost identical, but the performance is quite different.

              # Slower
          penguins.groupby('species').mean()['bill_length_mm']

          # Faster
          penguins.groupby('species')['bill_length_mm'].mean()

  • The groupby method is much quicker than for-looping over the DataFrame in Python. It can often produce results using just a single, fast pass over the data, updating the sum, mean, count, min, or other aggregate for each group along the way.

Beyond default aggregation methods¶

  • There are many built-in aggregation methods.
  • What if you want to apply different aggregation methods to different columns?
  • What if the aggregation method you want to use doesn't already exist in pandas?

The aggregate method¶

  • The DataFrameGroupBy object has a general aggregate method, which aggregates using one or more operations.
    • Remember, aggregation refers to the process of reducing many values to one.
  • There are many ways of using aggregate; refer to the documentation for a comprehensive list.
  • Example arguments:
    • A single function.
    • A list of functions.
    • A dictionary mapping column names to functions.
  • Per the documentation, agg is an alias for aggregate.

Example¶

How many penguins are there of each 'species', and what is the mean 'body_mass_g' of each species?

In [41]:
(penguins
 .groupby('species')
 ['body_mass_g']
 .aggregate(['count', 'mean'])
)
Out[41]:
count mean
species
Adelie 146 3706.16
Chinstrap 68 3733.09
Gentoo 119 5092.44

Note what happens when we don't select a column before aggregating.

In [42]:
(penguins
 .groupby('species')
 .aggregate(['count', 'mean'])
)
Out[42]:
bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
count mean count mean count mean count mean
species
Adelie 146 38.82 146 18.35 146 190.10 146 3706.16
Chinstrap 68 48.83 68 18.42 68 195.82 68 3733.09
Gentoo 119 47.57 119 15.00 119 217.24 119 5092.44

Example¶

What is the maximum 'bill_length_mm' of each species, and which 'island's is each 'species' found on?

In [43]:
(penguins
 .groupby('species')
 .aggregate({'bill_length_mm': 'max', 'island': 'nunique'})
)
Out[43]:
bill_length_mm island
species
Adelie 46.0 3
Chinstrap 58.0 1
Gentoo 59.6 1

Example¶

What is the interquartile range of the 'body_mass_g' of each 'species'?

In [44]:
# The function for .agg takes in a pd.Series as its argument and returns a scalar 
def iqr(series):
    return np.percentile(series, 75) - np.percentile(series, 25)

(penguins
 .groupby('species')
 ['body_mass_g']
 .agg(iqr)
)
Out[44]:
species
Adelie       637.5
Chinstrap    462.5
Gentoo       800.0
Name: body_mass_g, dtype: float64

Other DataFrameGroupBy methods¶

Split-apply-combine, revisited¶

When we introduced the split-apply-combine pattern, the "apply" step involved aggregation – our final DataFrame had one row for each group.

No description has been provided for this image

Instead of aggregating during the apply step, we could instead perform a:

  • Transformation, in which we perform operations to every value within each group.

  • Filtration, in which we keep only the groups that satisfy some condition.

Transformations¶

  • Suppose we want to convert the 'body_mass_g' column to to z-scores (i.e. standard units):
$$z(x_i) = \frac{x_i - \text{mean of } x}{\text{SD of } x}$$
In [45]:
def z_score(x):
    return (x - x.mean()) / x.std(ddof=0)
In [46]:
z_score(penguins['body_mass_g'])
Out[46]:
0     -0.57
1     -0.51
2     -1.19
4     -0.94
       ... 
340    0.80
341    1.92
342    1.23
343    1.48
Name: body_mass_g, Length: 333, dtype: float64

Transformations within groups¶

  • Now, what if we wanted the z-score within each group?

  • To do so, we can use the transform method on a DataFrameGroupBy object. The transform method takes in a function, which itself takes in a Series and returns a new Series.

  • A transformation produces a DataFrame or Series of the same size – it is not an aggregation!

In [47]:
z_mass = (penguins
          .groupby('species')
          ['body_mass_g']
          .transform(z_score))
z_mass
Out[47]:
0      0.10
1      0.21
2     -1.00
4     -0.56
       ... 
340   -0.49
341    1.32
342    0.22
343    0.62
Name: body_mass_g, Length: 333, dtype: float64
In [48]:
penguins.assign(z_mass=z_mass)
Out[48]:
species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g sex z_mass
0 Adelie Torgersen 39.1 18.7 181.0 3750.0 Male 0.10
1 Adelie Torgersen 39.5 17.4 186.0 3800.0 Female 0.21
2 Adelie Torgersen 40.3 18.0 195.0 3250.0 Female -1.00
4 Adelie Torgersen 36.7 19.3 193.0 3450.0 Female -0.56
... ... ... ... ... ... ... ... ...
340 Gentoo Biscoe 46.8 14.3 215.0 4850.0 Female -0.49
341 Gentoo Biscoe 50.4 15.7 222.0 5750.0 Male 1.32
342 Gentoo Biscoe 45.2 14.8 212.0 5200.0 Female 0.22
343 Gentoo Biscoe 49.9 16.1 213.0 5400.0 Male 0.62

333 rows × 8 columns

Note that below, penguin 340 has a larger 'body_mass_g' than penguin 0, but a lower 'z_mass'.

  • Penguin 0 has an above average 'body_mass_g' among 'Adelie' penguins.
  • Penguin 340 has a below average 'body_mass_g' among 'Gentoo' penguins. Remember from earlier that the average 'body_mass_g' of 'Gentoo' penguins is much higher than for other species.

Filtering Groups¶

  • To keep only the groups that satisfy a particular condition, use the filter method on a DataFrameGroupBy object.

  • The filter method takes in a function, which itself takes in a DataFrame/Series and return a single Boolean. The result is a new DataFrame/Series with only the groups for which the filter function returned True.

For example, suppose we want only the 'species' whose average 'bill_length_mm' is above 39.

In [49]:
(penguins
 .groupby('species')
 .filter(lambda df: df['bill_length_mm'].mean() > 39)
)
Out[49]:
species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g sex
152 Chinstrap Dream 46.5 17.9 192.0 3500.0 Female
153 Chinstrap Dream 50.0 19.5 196.0 3900.0 Male
154 Chinstrap Dream 51.3 19.2 193.0 3650.0 Male
155 Chinstrap Dream 45.4 18.7 188.0 3525.0 Female
... ... ... ... ... ... ... ...
340 Gentoo Biscoe 46.8 14.3 215.0 4850.0 Female
341 Gentoo Biscoe 50.4 15.7 222.0 5750.0 Male
342 Gentoo Biscoe 45.2 14.8 212.0 5200.0 Female
343 Gentoo Biscoe 49.9 16.1 213.0 5400.0 Male

187 rows × 7 columns

No more 'Adelie's!

Or, as another example, suppose we only want 'species' with at least 100 penguins:

In [50]:
penguins.groupby('species').filter(lambda df: df.shape[0] > 100)
Out[50]:
species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g sex
0 Adelie Torgersen 39.1 18.7 181.0 3750.0 Male
1 Adelie Torgersen 39.5 17.4 186.0 3800.0 Female
2 Adelie Torgersen 40.3 18.0 195.0 3250.0 Female
4 Adelie Torgersen 36.7 19.3 193.0 3450.0 Female
... ... ... ... ... ... ... ...
340 Gentoo Biscoe 46.8 14.3 215.0 4850.0 Female
341 Gentoo Biscoe 50.4 15.7 222.0 5750.0 Male
342 Gentoo Biscoe 45.2 14.8 212.0 5200.0 Female
343 Gentoo Biscoe 49.9 16.1 213.0 5400.0 Male

265 rows × 7 columns

No more 'Chinstrap's!

Grouping with multiple columns¶

When we group with multiple columns, one group is created for every unique combination of elements in the specified columns.

In [51]:
species_and_island = penguins.groupby(['species', 'island']).mean()
species_and_island
Out[51]:
bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
species island
Adelie Biscoe 38.98 18.37 188.80 3709.66
Dream 38.52 18.24 189.93 3701.36
Torgersen 39.04 18.45 191.53 3708.51
Chinstrap Dream 48.83 18.42 195.82 3733.09
Gentoo Biscoe 47.57 15.00 217.24 5092.44

Grouping and indexes¶

  • The groupby method creates an index based on the specified columns.
  • When grouping by multiple columns, the resulting DataFrame has a MultiIndex.
  • Advice: When working with a MultiIndex, use reset_index or set as_index=False in groupby.
In [52]:
species_and_island
Out[52]:
bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
species island
Adelie Biscoe 38.98 18.37 188.80 3709.66
Dream 38.52 18.24 189.93 3701.36
Torgersen 39.04 18.45 191.53 3708.51
Chinstrap Dream 48.83 18.42 195.82 3733.09
Gentoo Biscoe 47.57 15.00 217.24 5092.44
In [53]:
species_and_island['body_mass_g']
Out[53]:
species    island   
Adelie     Biscoe       3709.66
           Dream        3701.36
           Torgersen    3708.51
Chinstrap  Dream        3733.09
Gentoo     Biscoe       5092.44
Name: body_mass_g, dtype: float64
In [54]:
species_and_island.loc['Adelie']
Out[54]:
bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
island
Biscoe 38.98 18.37 188.80 3709.66
Dream 38.52 18.24 189.93 3701.36
Torgersen 39.04 18.45 191.53 3708.51
In [55]:
species_and_island.loc[('Adelie', 'Torgersen')]
Out[55]:
bill_length_mm         39.04
bill_depth_mm          18.45
flipper_length_mm     191.53
body_mass_g          3708.51
Name: (Adelie, Torgersen), dtype: float64
In [56]:
species_and_island.reset_index()
Out[56]:
species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
0 Adelie Biscoe 38.98 18.37 188.80 3709.66
1 Adelie Dream 38.52 18.24 189.93 3701.36
2 Adelie Torgersen 39.04 18.45 191.53 3708.51
3 Chinstrap Dream 48.83 18.42 195.82 3733.09
4 Gentoo Biscoe 47.57 15.00 217.24 5092.44
In [57]:
penguins.groupby(['species', 'island'], as_index=False).mean()
Out[57]:
species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
0 Adelie Biscoe 38.98 18.37 188.80 3709.66
1 Adelie Dream 38.52 18.24 189.93 3701.36
2 Adelie Torgersen 39.04 18.45 191.53 3708.51
3 Chinstrap Dream 48.83 18.42 195.82 3733.09
4 Gentoo Biscoe 47.57 15.00 217.24 5092.44

Discussion: Checking your knowledge¶

Find the most popular male and female baby name for each year in the dataset. Exclude years where there were fewer than 1 million births recorded.

In [58]:
baby = pd.read_csv('data/baby.csv')
baby
Out[58]:
Name Sex Count Year
0 Liam M 20456 2022
1 Noah M 18621 2022
2 Olivia F 16573 2022
3 Oliver M 15076 2022
... ... ... ... ...
2085154 Worthy M 5 1880
2085155 Wright M 5 1880
2085156 York M 5 1880
2085157 Zachariah M 5 1880

2085158 rows × 4 columns

In [59]:
# Fill me in

Pivot Tables: An extension of grouping¶

Pivot tables are a compact way to display tables for humans to read:

Sex F M
Year
2018 1698373 1813377
2019 1675139 1790682
2020 1612393 1721588
2021 1635800 1743913
2022 1628730 1733166
  • Notice that each value in the table is a sum over the counts, split by year and sex.
  • You can think of pivot tables as grouping using two columns, then "pivoting" one of the group keys into columns

pivot_table¶

The pivot_table DataFrame method aggregates a DataFrame using two columns. To use it:

df.pivot_table(index=index_col,
               columns=columns_col,
               values=values_col,
               aggfunc=func)

The resulting DataFrame will have:

  • One row for every unique value in index_col.
  • One column for every unique value in columns_col.
  • Values determined by applying func on values in values_col.
In [60]:
last_5_years = baby.query('Year >= 2018')
In [61]:
last_5_years.pivot_table(
    index='Year',
    columns='Sex',
    values='Count',
    aggfunc='sum',
)
Out[61]:
Sex F M
Year
2018 1698373 1813377
2019 1675139 1790682
2020 1612393 1721588
2021 1635800 1743913
2022 1628730 1733166
In [62]:
# Look at the similarity to the snippet above
(last_5_years
 .groupby(['Year', 'Sex'])
 ['Count']
 .sum()
 .unstack('Sex')
)
Out[62]:
Sex F M
Year
2018 1698373 1813377
2019 1675139 1790682
2020 1612393 1721588
2021 1635800 1743913
2022 1628730 1733166

Example:¶

Find the number of penguins per island and species.

In [63]:
penguins.pivot_table(
    index='species', 
    columns='island', 
    values='bill_length_mm', # Choice of column here doesn't actually matter
    aggfunc='count',
)
Out[63]:
island Biscoe Dream Torgersen
species
Adelie 44.0 55.0 47.0
Chinstrap NaN 68.0 NaN
Gentoo 119.0 NaN NaN

Note that there is a NaN at the intersection of 'Biscoe' and 'Chinstrap', because there were no Chinstrap penguins on Biscoe Island.

We can either use the fillna method afterwards or the fill_value argument to fill in NaNs.

In [64]:
penguins.pivot_table(
    index='species', 
    columns='island', 
    values='bill_length_mm', 
    aggfunc='count',
    fill_value=0,
)
Out[64]:
island Biscoe Dream Torgersen
species
Adelie 44 55 47
Chinstrap 0 68 0
Gentoo 119 0 0

Granularity, revisited¶

Take another look at the pivot table from the previous cell. Each row of the original penguins represented a single penguin, and each column represented features of the penguins.

What is the granularity of this table?

In [65]:
penguins.pivot_table(
    index='species', 
    columns='island', 
    values='bill_length_mm', 
    aggfunc='count',
    fill_value=0,
)
Out[65]:
island Biscoe Dream Torgersen
species
Adelie 44 55 47
Chinstrap 0 68 0
Gentoo 119 0 0

Reshaping¶

  • pivot_table reshapes DataFrames from "long" to "wide".
  • Other DataFrame reshaping methods:
    • melt: Un-pivots a DataFrame. Very useful in data cleaning.
    • pivot: Like pivot_table, but doesn't do aggregation.
    • stack: Pivots multi-level columns to multi-indices.
    • unstack: Pivots multi-indices to columns.
    • Google and the documentation are your friends!

Distributions¶

Joint distribution¶

When using aggfunc='count', a pivot table describes the joint distribution of two categorical variables. This is also called a contingency table.

In [66]:
counts = penguins.pivot_table(
    index='species', 
    columns='sex', 
    values='body_mass_g', 
    aggfunc='count', 
    fill_value=0
)
counts
Out[66]:
sex Female Male
species
Adelie 73 73
Chinstrap 34 34
Gentoo 58 61

We can normalize the DataFrame by dividing by the total number of penguins. The resulting numbers can be interpreted as probabilities that a randomly selected penguin from the dataset belongs to a given combination of species and sex.

In [67]:
joint = counts / counts.sum().sum()
joint
Out[67]:
sex Female Male
species
Adelie 0.22 0.22
Chinstrap 0.10 0.10
Gentoo 0.17 0.18

Marginal probabilities¶

If we sum over one of the axes, we can compute marginal probabilities, i.e. unconditional probabilities.

In [68]:
joint
Out[68]:
sex Female Male
species
Adelie 0.22 0.22
Chinstrap 0.10 0.10
Gentoo 0.17 0.18
In [69]:
# Recall, joint.sum(axis=0) sums across the rows, which computes the sum of the **columns**.
joint.sum(axis=0)
Out[69]:
sex
Female    0.5
Male      0.5
dtype: float64
In [70]:
joint.sum(axis=1)
Out[70]:
species
Adelie       0.44
Chinstrap    0.20
Gentoo       0.36
dtype: float64

For instance, the second Series tells us that a randomly selected penguin has a 0.36 chance of being of species 'Gentoo'.

Conditional probabilities¶

Using counts, how might we compute conditional probabilities like $$P(\text{species } = \text{"Adelie"} \mid \text{sex } = \text{"Female"})?$$

In [71]:
counts
Out[71]:
sex Female Male
species
Adelie 73 73
Chinstrap 34 34
Gentoo 58 61
$$\begin{align*} P(\text{species} = c \mid \text{sex} = x) &= \frac{P(\text{species} = c \text{ and } \text{sex} = x)}{P(\text{sex = }x)} \\ &= \frac{\frac{\# \: (\text{species } = \: c \text{ and } \text{sex } = \: x)}{N}}{\frac{\# \: (\text{sex } = \: x)}{N}} \\ &= \frac{\# \: (\text{species} = c \text{ and } \text{sex} = x)}{\# \: (\text{sex} = x)} \end{align*}$$

Answer: To find conditional probabilities of species given sex, divide by column sums. To find conditional probabilities of sex given species, divide by row sums.

Conditional probabilities¶

To find conditional probabilities of species given sex, divide by column sums. To find conditional probabilities of sex given species, divide by row sums.

In [72]:
counts
Out[72]:
sex Female Male
species
Adelie 73 73
Chinstrap 34 34
Gentoo 58 61
In [73]:
counts.sum(axis=0)
Out[73]:
sex
Female    165
Male      168
dtype: int64

The conditional distribution of species given sex is below. Note that in this new DataFrame, the 'Female' and 'Male' columns each sum to 1.

In [74]:
counts / counts.sum(axis=0)
Out[74]:
sex Female Male
species
Adelie 0.44 0.43
Chinstrap 0.21 0.20
Gentoo 0.35 0.36

For instance, the above DataFrame tells us that the probability that a randomly selected penguin is of species 'Adelie' given that they are of sex 'Female' is 0.442424.

Exercise: Try and find the conditional distribution of sex given species.

In [ ]:

Simpson's paradox¶

No description has been provided for this image

Example: Grades¶

  • Two students, Lisa and Bart, just finished freshman year. They both took a different number of classes in Fall, Winter, and Spring.

  • Each quarter, Lisa had a higher GPA than Bart.

  • But Bart has a higher overall GPA.

  • How is this possible? 🤔

Run this cell to create DataFrames that contain each students' grades.

In [75]:
lisa = pd.DataFrame([
        [20, 46],
        [18, 54],
        [5, 20],
    ],
    columns=['Units', 'Grade Points Earned'], 
    index=['Fall', 'Winter', 'Spring'],
)

bart = pd.DataFrame([
        [5, 10],
        [5, 13.5],
        [22, 81.4],
    ],
    columns=['Units', 'Grade Points Earned'], 
    index=['Fall', 'Winter', 'Spring'],
)

Quarter-specific vs. overall GPAs¶

Note: The number of "grade points" earned for a course is

$$\text{number of units} \cdot \text{grade (out of 4)}$$

For instance, an A- in a 4 unit course earns $3.7 \cdot 4 = 14.8$ grade points.

In [76]:
lisa
Out[76]:
Units Grade Points Earned
Fall 20 46
Winter 18 54
Spring 5 20
In [77]:
bart
Out[77]:
Units Grade Points Earned
Fall 5 10.0
Winter 5 13.5
Spring 22 81.4

Lisa had a higher GPA in all three quarters:

In [78]:
quarterly_gpas = pd.DataFrame({
    "Lisa's Quarter GPA": lisa['Grade Points Earned'] / lisa['Units'],
    "Bart's Quarter GPA": bart['Grade Points Earned'] / bart['Units'],
})

quarterly_gpas
Out[78]:
Lisa's Quarter GPA Bart's Quarter GPA
Fall 2.3 2.0
Winter 3.0 2.7
Spring 4.0 3.7

But Lisa's overall GPA was less than Bart's overall GPA:

In [79]:
tot = lisa.sum()
tot['Grade Points Earned'] / tot['Units']
Out[79]:
2.7906976744186047
In [80]:
tot = bart.sum()
tot['Grade Points Earned'] / tot['Units']
Out[80]:
3.278125

What happened?¶

In [81]:
(quarterly_gpas
 .assign(Lisa_units=lisa['Units'],
         Bart_units=bart['Units']) 
 .iloc[:, [0, 2, 1, 3]]
)
Out[81]:
Lisa's Quarter GPA Lisa_units Bart's Quarter GPA Bart_units
Fall 2.3 20 2.0 5
Winter 3.0 18 2.7 5
Spring 4.0 5 3.7 22

  • When Lisa and Bart both performed poorly, Lisa took more units than Bart. This brought down 📉 Lisa's overall average.

  • When Lisa and Bart both performed well, Bart took more units than Annie. This brought up 📈 Bart's overall average.

Simpson's paradox¶

  • Simpson's paradox occurs when grouped data and ungrouped data show opposing trends.

    • It is named after Edward H. Simpson, not Lisa or Bart Simpson.

  • It is purely arithmetic – it is a consequence of weighted averages.

  • It often happens because there is a hidden factor (i.e. a confounder) within the data that influences results.

  • Question: What is the "correct" way to summarize your data? What if you had to act on these results?

Example: How Berkeley was almost sued for gender discrimination (1973)¶

What do you notice?

No description has been provided for this image
In [82]:
show_paradox_slides()

What happened?¶

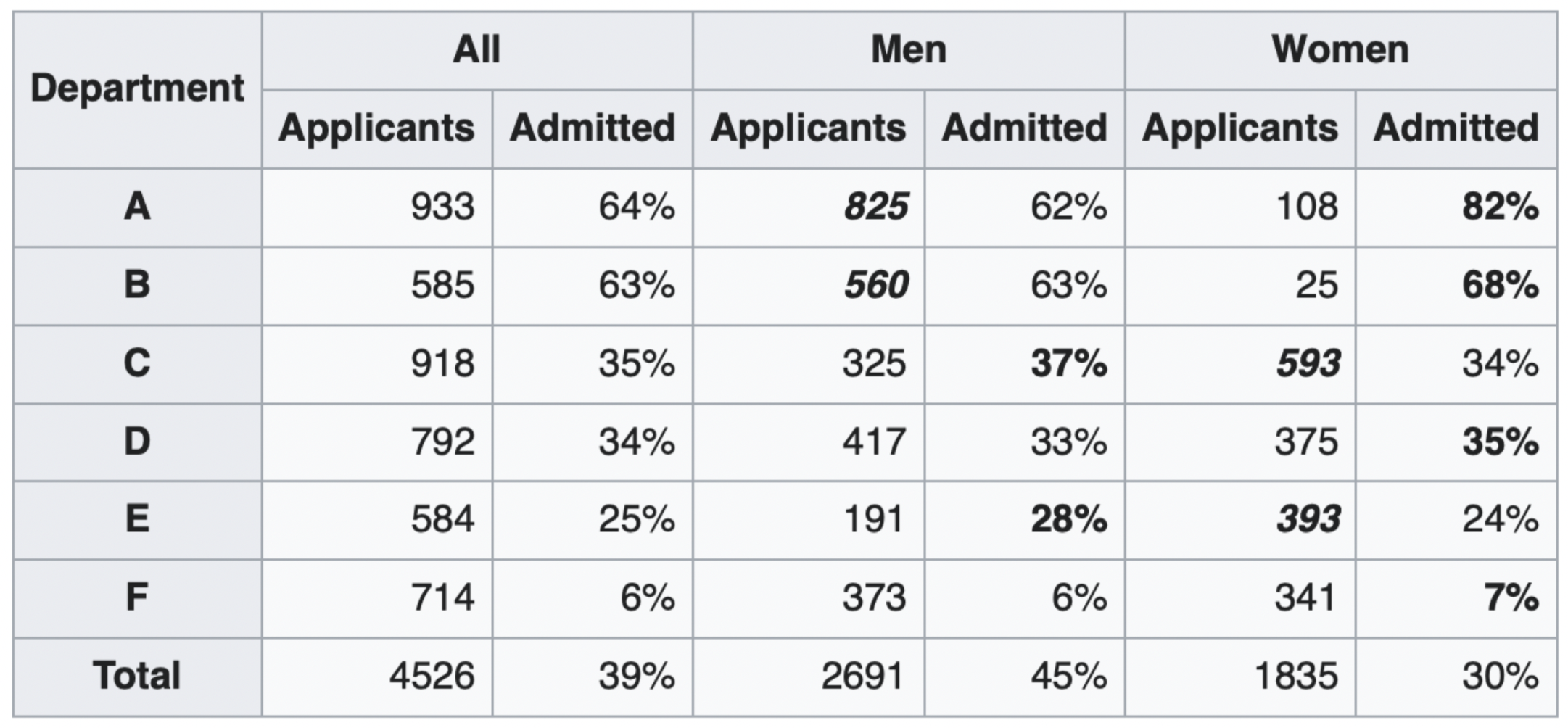
  • The overall acceptance rate for women (30%) was lower than it was for men (45%).

  • However, most departments (A, B, D, F) had a higher acceptance rate for women.

  • Department A had a 62% acceptance rate for men and an 82% acceptance rate for women!

    • 31% of men applied to Department A.
    • 6% of women applied to Department A.

  • Department F had a 6% acceptance rate for men and a 7% acceptance rate for women!

    • 14% of men applied to Department F.
    • 19% of women applied to Department F.

  • Conclusion: Women tended to apply to departments with a lower acceptance rate; the data don't support the hypothesis that there was major gender discrimination against women.

Caution!¶

This doesn't mean that admissions are free from gender discrimination!

From Moss-Racusin et al., 2012, PNAS (cited 2600+ times):

In a randomized double-blind study (n = 127), science faculty from research-intensive universities rated the application materials of a student—who was randomly assigned either a male or female name—for a laboratory manager position. Faculty participants rated the male applicant as significantly more competent and hireable than the (identical) female applicant. These participants also selected a higher starting salary and offered more career mentoring to the male applicant. The gender of the faculty participants did not affect responses, such that female and male faculty were equally likely to exhibit bias against the female student.

But then...¶

From Williams and Ceci, 2015, PNAS:

Here we report five hiring experiments in which faculty evaluated hypothetical female and male applicants, using systematically varied profiles disguising identical scholarship, for assistant professorships in biology, engineering, economics, and psychology. Contrary to prevailing assumptions, men and women faculty members from all four fields preferred female applicants 2:1 over identically qualified males with matching lifestyles (single, married, divorced), with the exception of male economists, who showed no gender preference.

Do these conflict?¶

Not necessarily. One explanation, from William and Ceci:

Instead, past studies have used ratings of students’ hirability for a range of posts that do not include tenure-track jobs, such as managing laboratories or performing math assignments for a company. However, hiring tenure-track faculty differs from hiring lower-level staff: it entails selecting among highly accomplished candidates, all of whom have completed Ph.D.s and amassed publications and strong letters of support. Hiring bias may occur when applicants’ records are ambiguous, as was true in studies of hiring bias for lower-level staff posts, but such bias may not occur when records are clearly strong, as is the case with tenure-track hiring.

Do these conflict?¶

From Witteman, et al, 2019, in The Lancet:

Thus, evidence of scientists favouring women comes exclusively from hypothetical scenarios, whereas evidence of scientists favouring men comes from hypothetical scenarios and real behaviour. This might reflect academics' growing awareness of the social desirability of achieving gender balance, while real academic behaviour might not yet put such ideals into action.

Example: Restaurant reviews and phone types¶

  • You are deciding whether to eat at Dirty Birds or The Loft.

  • Suppose Yelp shows ratings aggregated by phone type (Android vs. iPhone).

Phone Type Stars for Dirty Birds Stars for The Loft
Android 4.24 4.0
iPhone 2.99 2.79
All 3.32 3.37

  • Question: Should you choose Dirty Birds or The Loft?

  • Answer: The type of phone you use likely has nothing to do with your taste in food – pick the restaurant that is rated higher overall.

  • Remember, Simpson's paradox is merely a property of weighted averages!

Takeaways¶

Be skeptical of...

  • Aggregate statistics.
  • People misusing statistics to "prove" that discrimination doesn't exist.
  • Drawing conclusions from individual publications ($p$-hacking, publication bias, narrow focus, etc.).
  • Everything!

We need to apply domain knowledge and human judgement calls to decide what to do when Simpson's paradox is present.

Really?¶

To handle Simpson's paradox with rigor, we need some ideas from causal inference which we don't have time to cover in DSC 80. This video has a good example of how to approach Simpson's paradox, using a minimal amount of causal inference, if you're curious (not required for DSC 80).

In [83]:
IFrame('https://www.youtube-nocookie.com/embed/zeuW1Z2EtLs?si=l2Dl7P-5RCq3ODpo',
       width=560, height=315)
Out[83]:

Further reading¶

  • Gender Bias in Admission Statistics?
    • Contains a great visualization, but seems to be paywalled now.
  • What is Simpson's Paradox?

Summary, next time¶

  • Grouping allows us to change the level of granularity in a DataFrame.
  • Grouping involves three steps – split, apply, and combine (or filter, or transform).
  • pivot_table aggregates data based on two categorical columns, and reshapes the result to be "wide" instead of "long".
  • Simpson's paradox occurs when grouped data and ungrouped data show opposing trends.
    • It is a consequence of arithmetic.
  • Next time: Data cleaning! 🧼