In [1]:
from dsc80_utils import *

Lecture 6 – Hypothesis Testing¶

DSC 80, Fall 2023¶

📣 Announcements 📣¶

  • Good job on Project 1!
  • Lab 3 due on Mon.

📆 Agenda¶

  • Data scope
  • What is hypothesis testing? (Review from DSC 10)
  • Why is hypothesis testing confusing to learn?
  • Hypothesis testing examples
    • Coin flipping
    • Total variation distance
    • Permutation testing
  • Student-submitted hypothesis testing questions

Data Scope¶

  • Target population: All elements of the population you ultimately want to draw conclusions about.
  • Access frame: All elements that are accessible for you for measurement and observation.
  • Sample: Subset of the access frame that you observed / measured.

Example: Wikipedia Awards¶

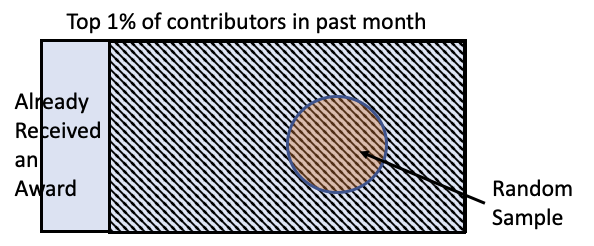
  • A 2012 paper asked: if we give awards to Wikipedia contributors, will they contribute more?
    • Took top 1% of of Wikipedia contributors, excluded people who already received an award, then took a random sample of 200 contributors.
No description has been provided for this image

Example: Who will win the election?¶

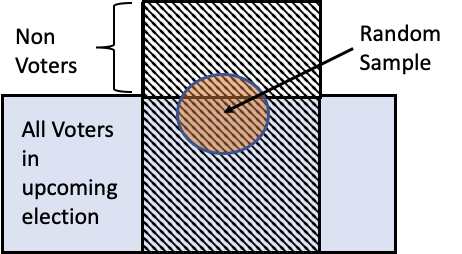
  • 2016 US Presidental Election: most pollsters predicted Clinton to win over Trump.
    • Randomly selected people and asked them a question over the phone.
No description has been provided for this image

🔑 Key Idea: Random samples look like the access frame they were sampled from¶

  • This enables statistical inference!
  • But keep in mind, random samples look like their access frame, which can be different than the population itself.

What is Hypothesis Testing? (Review from DSC 10)¶

  • One common way to use your sample to draw conclusions about your population (Understanding the World).
    • Other common method is to use confidence intervals.
No description has been provided for this image

The Basics¶

  • Experiment done, or found something interesting in data.
    • Created a new vaccine, ran experiment comparing it to a placebo.
  • Want to "prove" that your treatment works.
    • Or your data actually show an interesting pattern, etc.
  • So you want compare your data against a reasonable baseline.
  • Hypothesis testing: way to quantitively describe how "different" your data is from a baseline.
    • In DSC 10, $ p < 0.05 $ means that data looks different enough to act on.

Hypothesis Testing Setup¶

No description has been provided for this image No description has been provided for this image

Why is Hypothesis Testing Hard to Learn?¶

  • You'll probably be confused this time, too!

Philosophical reasons:

  • It's like "proof by contradiction":
    • If I want to show that my vaccine works, I consider a world where it doesn't (null hypothesis).
    • Then, I "attack the baseline" by showing that under the null hypothesis my data would be very unlikely.
  • Showing something is not true is a lot easier than showing something is true!

Technical reasons:

  • Several choices to make:
    • What a good null hypothesis is.
    • Test statistic.
    • How to simulate more samples from the null population.
    • Whether to look at the left tail or right tail of sampling distribution.
  • Good news: almost all hypothesis tests follow this format!

Example: Coin flipping¶

Coin flipping¶

Suppose that we flipped a coin 100 times, and we saw 59 heads. We want to show that the coin is biased in favor of heads:

  • Observation: We flipped a coin 100 times, and saw 59 heads and 41 tails.

  • Null Hypothesis: The coin is fair.

  • Alternative Hypothesis: The coin is biased in favor of heads.

  • Test Statistic: Number of heads, $N_H$.

Generating the null distribution¶

  • Now that we've chosen a test statistic, we need to generate the distribution of the test statistic under the assumption the null hypothesis is true, i.e. the null distribution.

  • This distribution will give us, for instance:

    • The probability of seeing 4 heads in 100 flips of a fair coin.
    • The probability of seeing at most 46 heads in 100 flips of a fair coin.
    • The probability of seeing at least 59 heads in 100 flips of a fair coin.

Generating the null distribution, using math¶

The number of heads in 100 flips of a fair coin follows the $\text{Binomial(100, 0.5)}$ distribution, in which

$$P(\text{# heads} = k) = {100 \choose k} (0.5)^k{(1-0.5)^{100-k}} = {100 \choose k} 0.5^{100}$$
In [2]:
from scipy.special import comb

def p_k_heads(k):
    return comb(100, k) * (0.5) ** 100

The probability that we see at least 59 heads is then:

In [3]:
sum([p_k_heads(k) for k in range(59, 101)])
Out[3]:
0.04431304005703377

Let's look at this distribution visually.

In [6]:
# Also, this line tells pandas to generate plotly plots by default!
pd.options.plotting.backend = 'plotly'
In [11]:
plot_df = pd.DataFrame().assign(k = range(101))
plot_df['p_k'] = p_k_heads(plot_df['k'])
plot_df['color'] = plot_df['k'].apply(lambda k: 'orange' if k >= 59 else 'blue')

fig = plot_df.plot(kind='bar', x='k', y='p_k', color='color', width=1000)
fig
# fig.add_annotation(text='This orange area is the p-value!', x=77, y=0.008, showarrow=False)

Making a decision¶

We saw that, in 100 flips of a fair coin, $P(\text{# heads} \geq 59)$ is only ~4.4%.

  • This is quite low – it suggests that our observed result is quite unlikely under the null.

  • As such, we will reject the null hypothesis – our observation is not consistent with the hypothesis that the coin is fair.

  • The null still may be true – it's possible that the coin we flipped was fair, and we just happened to see a rare result. For the same reason, we also cannot "accept" the alternative.

  • This probability – the probability of seeing a result at least as extreme as the observed, under the null hypothesis – is called the p-value.

    • If the p-value is below a pre-defined cutoff (often 5%), we reject the null.
    • Otherwise, we fail to reject the null.

⚠️ We can't "accept" the null!¶

  • Note that we are very careful in saying that we either reject the null or fail to reject the null.

  • Just because we fail to reject the null, it doesn't mean the null is true – we cannot "accept" it.

  • Example:

    • Suppose there is a coin that is truly biased towards heads, with probability 0.55.
    • We flip it 10 times and see 5 heads and 5 tails.
    • If we conduct a hypothesis test where the null is that the coin is fair, we will fail to reject the null.
    • But the null isn't true.

In our framework:¶

No description has been provided for this image No description has been provided for this image

Generating the null distribution, using simulation¶

  • In the most recent example, we computed the true probability distribution of the test statistic under the null hypothesis.

  • We could only do this because we know that the number of heads in $N$ flips of a fair coin follows the $\text{Binomial}(N, 0.5)$ distribution.

  • Often, we'll pick test statistics for which we don't know the true probability distribution. In such cases, we'll have to simulate, as we did in DSC 10.

  • Simulations provide us with empirical distributions of test statistics; if we simulate with a large (>= 10,000) number of repetitions, the empirical distribution of the test statistic should look similar to the true probability distribution of the test statistic.

Generating the null distribution, using simulation¶

First, let's figure out how to perform one instance of the experiment – that is, how to flip 100 coins once. Recall, to sample from a categorical distribution, we use np.random.multinomial.

In [13]:
# Flipping a fair coin 100 times.
# Interpret the result as [Heads, Tails].
np.random.multinomial(100, [0.5, 0.5])
Out[13]:
array([53, 47])

Then, we can repeat it a large number of times.

In [14]:
# 100,000 times, we want to flip a coin 100 times.
results = []

for _ in range(100_000):
    num_heads = np.random.multinomial(100, [0.5, 0.5])[0]
    results.append(num_heads)

Each entry in results is the number of heads in 100 simulated coin flips.

In [15]:
results[:10]
Out[15]:
[50, 44, 48, 47, 47, 54, 38, 47, 48, 48]

Visualizing the empirical distribution of the test statistic¶

In [17]:
fig = px.histogram(pd.DataFrame(results), x=0, nbins=50, histnorm='probability', 
                   title='Empirical Distribution of # Heads in 100 Flips of a Fair Coin')
fig.add_vline(x=59, line_color='red')
fig.update_layout(xaxis_range=[0, 100])

Again, we can compute the p-value, which is the probability of seeing a result as or more extreme than the observed, under the null.

In [18]:
(np.array(results) >= 59).mean()
Out[18]:
0.04391

Note that this number is close, but not identical, to the true p-value we found before. That's because we computed this p-value using a simulation, and hence an approximation.

In our framework:¶

No description has been provided for this image No description has been provided for this image

Reflection¶

Can we make things faster? 🏃¶

A mantra so far in this course has been avoid for-loops whenever possible. That applies here, too.

np.random.multinomial (and np.random.choice) accepts a size argument. By providing size=100_000, we can tell numpy to draw 100 elements from a uniform distribution, 100_000 times, without needing a for-loop!

In [19]:
# An array with 100000 rows and 2 columns.
np.random.multinomial(100, [0.5, 0.5], size=100_000)
Out[19]:
array([[55, 45],
       [45, 55],
       [48, 52],
       ...,
       [53, 47],
       [50, 50],
       [50, 50]])
In [20]:
# Just the first column of the above array. Note the iloc-like syntax.
np.random.multinomial(100, [0.5, 0.5], size=100_000)[:, 0]
Out[20]:
array([45, 55, 38, ..., 53, 47, 50])
In [21]:
%%time

faster_results = np.random.multinomial(100, [0.5, 0.5], size=100_000)[:, 0]

CPU times: user 13 ms, sys: 1.67 ms, total: 14.7 ms
Wall time: 12.6 ms

The above approach is orders of magnitude faster than the for-loop approach! With that said, you are still allowed to use for-loops for hypothesis (and permutation) tests on assignments.

In [22]:
%%time

# 100,000 times, we want to flip a coin 100 times.
results = []

for _ in range(100_000):
    num_heads = np.random.multinomial(100, [0.5, 0.5])[0]
    results.append(num_heads)

CPU times: user 1.61 s, sys: 19.5 ms, total: 1.63 s
Wall time: 1.62 s

Choosing alternative hypotheses and test statistics¶

  • The alternative hypothesis we chose was the coin is biased in favor of heads, and the test statistic we chose was the number of heads, $N_H$.

  • We could've also chosen one the following options; each of them has the quality that large values point to one hypothesis, and small values point to the other:

    • $\frac{N_H}{100}$, the proportion of heads.
    • $N_H - 50$, the difference from the expected number of heads.

  • What if our alternative hypothesis was the coin is biased (either towards heads or tails)?

Absolute test statistics¶

For the alternative hypothesis "the coin is biased", one test statistic we could use is $|N_H - \frac{N}{2}|$, the absolute difference from the expected number of heads.

  • If this test statistic is large, it means that there were many more heads than expected, or many fewer heads than expected. If this test statistic is small, it means that the number of heads was close to expected.

  • For instance, suppose we flip 100 coins, and I tell you the absolute difference from the expected number of heads is 20.

  • Then, either we flipped 70 heads or 30 heads.

  • If our alternative hypothesis is that the coin was biased, then it doesn't matter in which direction it was biased, and this test statistic works.

  • But if our alternative hypothesis is that the coin was biased towards heads, then this is not helpful, because we don't know whether or not there were 70 heads (evidence for the alternative) or 30 heads (not evidence for the alternative).

Important¶

We'd like to choose a test statistic such that large values of the test statistic correspond to one hypothesis, and small values correspond to the other.

In other words, we'll try to avoid "two-tailed tests". Rough rule of thumb:

  • If the alternative hypothesis is "A > B", then the test statistic should measure differences and should not contain an absolute value.

  • If the alternative hypothesis is "A and B are different", then the test statistic should measure distances and should contain an absolute value.

Fun fact¶

  • One researcher found that coin flips aren't 50/50, but rather are closer to 51/49, biased towards whichever side started facing up.
  • Read this for more details.

Example: Total variation distance¶

Ethnic distribution of California vs. UCSD¶

The DataFrame below contains the ethnic breakdown of the state as a whole (source) and UCSD as of 2016 (source).

In [21]:
eth = pd.DataFrame(
    [['Asian', 0.15, 0.51],
     ['Black', 0.05, 0.02],
     ['Latino', 0.39, 0.16],
     ['White', 0.35, 0.2],
     ['Other', 0.06, 0.11]],
    columns=['Ethnicity', 'California', 'UCSD']
).set_index('Ethnicity')

eth
Out[21]:
California UCSD
Ethnicity
Asian 0.15 0.51
Black 0.05 0.02
Latino 0.39 0.16
White 0.35 0.20
Other 0.06 0.11
  • We want to decide whether UCSD students were drawn at random from the state of California.
  • The two categorical distributions above are clearly different. But how different are they?

Is the difference between the two distributions significant?¶

Let's establish our hypotheses.

  • Null Hypothesis: UCSD students were selected at random from the population of California residents.
  • Alternative Hypothesis: UCSD students were not selected at random from the population of California residents.
  • Observation: Ethnic distribution of UCSD students.
  • Test Statistic: We need a way of quantifying how different two categorical distributions are.
In [20]:
eth.plot(kind='barh', title='Ethnic Distribution of California and UCSD', barmode='group')

Total variation distance¶

The total variation distance (TVD) is a test statistic that describes the distance between two categorical distributions.

If $A = [a_1, a_2, ..., a_k]$ and $B = [b_1, b_2, ..., b_k]$ are both categorical distributions, then the TVD between $A$ and $B$ is

$$\text{TVD}(A, B) = \frac{1}{2} \sum_{i = 1}^k |a_i - b_i|$$
In [22]:
def total_variation_distance(dist1, dist2):
    '''Given two categorical distributions, 
    both sorted with same categories, calculates the TVD'''
    return np.sum(np.abs(dist1 - dist2)) / 2

Let's compute the TVD between UCSD's ethnic distribution and California's ethnic distribution.

In [23]:
observed_tvd = total_variation_distance(eth['UCSD'], eth['California'])
observed_tvd
Out[23]:
0.41000000000000003

The issue is we don't know whether this is a large value or a small value – we don't know where it lies in the distribution of TVDs under the null.

The plan¶

To conduct our hypothesis test, we will:

  • Repeatedly generate samples of size 30,000 (number of UCSD students) from the ethnic distribution of all of California.

  • Each time, compute the TVD between the simulated distribution and California's distribution.

  • This will generate an empirical distribution of TVDs, under the null.

  • Finally, determine whether the observed TVD is consistent with the empirical distribution of TVDs.

Generating one random sample¶

Again, to sample from a categorical distribution, we use np.random.multinomial.

Important: We must sample from the "population" distribution here, which is the ethnic distribution of everyone in California.

In [24]:
# Number of students at UCSD in this example.
N_STUDENTS = 30_000
In [25]:
eth['California']
Out[25]:
Ethnicity
Asian     0.15
Black     0.05
Latino    0.39
White     0.35
Other     0.06
Name: California, dtype: float64
In [26]:
np.random.multinomial(N_STUDENTS, eth['California'])
Out[26]:
array([ 4478,  1538, 11699, 10543,  1742])
In [27]:
np.random.multinomial(N_STUDENTS, eth['California']) / N_STUDENTS
Out[27]:
array([0.15, 0.05, 0.39, 0.35, 0.06])

Generating many random samples¶

We could write a for-loop to repeat the process on the previous slide repeatedly (and you can in labs and projects). However, we now know about the size argument in np.random.multinomial, so let's use that here.

In [28]:
num_reps = 100_000
eth_draws = np.random.multinomial(N_STUDENTS, eth['California'], size=num_reps) / N_STUDENTS
eth_draws
Out[28]:
array([[0.15, 0.05, 0.39, 0.35, 0.06],
       [0.15, 0.05, 0.39, 0.35, 0.06],
       [0.15, 0.05, 0.39, 0.35, 0.06],
       ...,
       [0.15, 0.05, 0.39, 0.35, 0.06],
       [0.15, 0.05, 0.39, 0.35, 0.06],
       [0.15, 0.05, 0.39, 0.35, 0.06]])
In [29]:
eth_draws.shape
Out[29]:
(100000, 5)

Notice that each row of eth_draws sums to 1, because each row is a simulated categorical distribution.

Computing many TVDs, without a for-loop¶

One issue is that the total_variation_distance function we've defined won't work with eth_draws (unless we use a for-loop), so we'll have to compute the TVD again.

In [30]:
tvds = np.sum(np.abs(eth_draws - eth['California'].to_numpy()), axis=1) / 2
tvds
Out[30]:
array([0.  , 0.  , 0.  , ..., 0.01, 0.  , 0.  ])

Just to make sure we did things correctly, we can compute the TVD between the first row of eth_draws and eth['California'] using our previous function.

In [31]:
# Note that this is the same as the first element in tvds.
total_variation_distance(eth_draws[0], eth['California'])
Out[31]:
0.003033333333333346

Visualizing the empirical distribution of the test statistic¶

In [34]:
observed_tvd
Out[34]:
0.41000000000000003
In [33]:
fig = px.histogram(pd.DataFrame(tvds), x=0, nbins=20, histnorm='probability', 
                   title='Empirical Distribution of the TVD')
# fig.add_vline(x=observed_tvd, line_color='red')
fig
In [37]:
(np.array(tvds) >= observed_tvd).mean()
Out[37]:
0.0

No, there's not a mistake in our code!

Conclusion¶

  • The chance that the observed TVD came from the distribution of TVDs under the null is essentially 0.
  • This matches our intuition from the start – the two distributions looked very different to begin with. But now we're quite sure the difference can't be explained solely due to chance.

In our framework:¶

No description has been provided for this image No description has been provided for this image

Summary of the method¶

To assess whether an "observed sample" was drawn randomly from a known categorical distribution:

  • Use the TVD as the test statistic because it measures the distance between two categorical distributions.
  • Sample at random from the population. Compute the TVD between each random sample and the known distribution to get an idea for what reasonable deviations from the eligible pool look like. Repeat this process many, many times.
  • Compare:
    • the empirical distribution of TVDs, with
    • the observed TVD from the sample.

Aside¶

  • It was probably obvious that the difference is significant even before running a hypothesis test.

  • Why? There are 30,000 students. Such a difference in proportion is unlikely to be due to random chance (something more systematic at play).

  • But what if N_STUDENTS = 300, N_STUDENTS = 30, or N_STUDENTS=3?

Discussion Question¶

At what value of N_STUDENTS would we fail to reject the null (at a 0.05 p-value cutoff)?

In [ ]:

The hypothesis testing "recipe"¶

Faced with a question about the data raised by an observation...

  1. Carefully pose the question as a testable "yes or no" hypothesis.
  2. Decide on a test statistic that helps differentiate between instances that would affirm or reject the hypothesis.
  3. Create a probability model for the data generating process that reflects the baseline that you want to compare against.
  4. Simulate the data generating process using this probability model (the "null hypothesis").
  5. Assess if the observation is consistent with the simulations by computing a p-value.

Hypothesis testing vs. permutation testing¶

So far, we've been able to simulate draws from the null population directly:

No description has been provided for this image No description has been provided for this image

But what if you have two samples and no information about any population distribution. Want to ask: are these two samples different? Do these samples look like they were drawn from the same population?

That's where permutation testing comes in.

Example: Birth weight and smoking 🚬¶

*Note*: For familiarity, we'll start with an example from DSC 10. This means we'll move quickly!

Birth weight and smoking 🚬¶

Let's start by loading in the data.

In [52]:
baby = pd.read_csv('data/babyweights.csv')
baby
Out[52]:
Birth Weight Gestational Days Maternal Age Maternal Height Maternal Pregnancy Weight Maternal Smoker
0 120 284 27 62 100 False
1 113 282 33 64 135 False
2 128 279 28 64 115 True
... ... ... ... ... ... ...
1171 130 291 30 65 150 True
1172 125 281 21 65 110 False
1173 117 297 38 65 129 False

1174 rows × 6 columns

We're only interested in the 'Birth Weight' and 'Maternal Smoker' columns.

In [53]:
baby = baby[['Maternal Smoker', 'Birth Weight']]
baby.head()
Out[53]:
Maternal Smoker Birth Weight
0 False 120
1 False 113
2 True 128
3 True 108
4 False 136

Note that there are two samples:

  • Birth weights of smokers' babies.
  • Birth weights of non-smokers' babies.

Exploratory data analysis¶

How many babies are in each group? What is the average birth weight within each group?

In [54]:
baby.groupby('Maternal Smoker')['Birth Weight'].agg(['mean', 'count'])
Out[54]:
mean count
Maternal Smoker
False 123.09 715
True 113.82 459

Note that 16 ounces are in 1 pound, so the above weights are ~7-8 pounds.

Visualizing birth weight distributions¶

Below, we draw the distributions of both sets of birth weights.

In [56]:
px.histogram(baby, color='Maternal Smoker', histnorm='probability', marginal='box', 
             title="Birth Weight by Mother's Smoking Status", barmode='overlay', opacity=0.7)

There appears to be a difference, but can it be attributed to random chance?

Hypothesis test setup¶

  • Null Hypothesis: In the population, birth weights of smokers' babies and non-smokers' babies have the same distribution, and the observed differences in our samples are due to random chance.

  • Alternative Hypothesis: In the population, smokers' babies have lower birth weights than non-smokers' babies, on average. The observed difference in our samples cannot be explained by random chance alone.

  • Issue: We don't know what the population distribution actually is – so how do we draw samples from it?

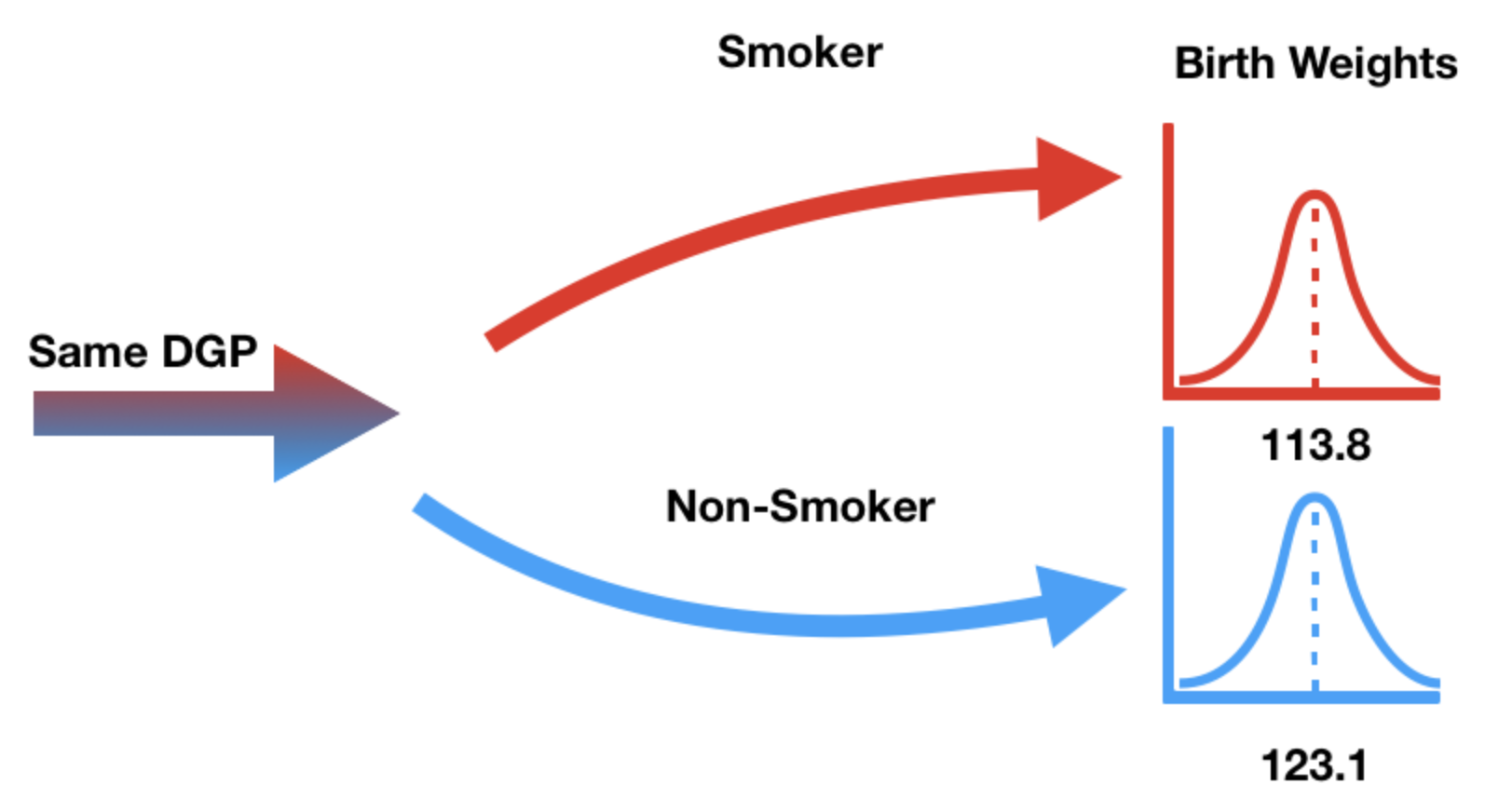
Null hypothesis: birth weights come from the same distribution¶

  • Our null hypothesis states that "smoker" / "non-smoker" labels have no relationship to birth weight.
  • In other words, the "smoker" / "non-smoker" labels may well have been assigned at random.
  • (DGP stands for Data-Generating Process)
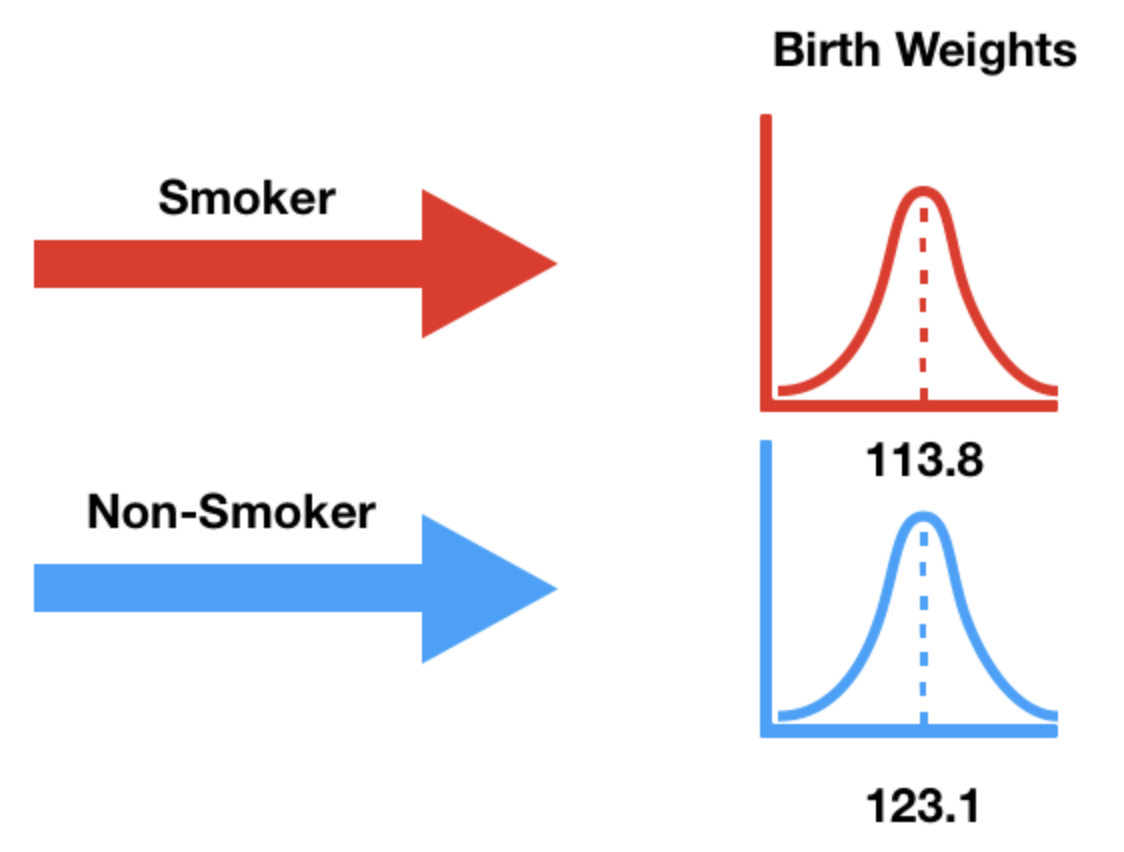
No description has been provided for this image

Alternative hypothesis: birth weights come from different distributions¶

  • Our alternative hypothesis states that the birth weights weights of smokers' babies and non-smokers' babies come from different population distributions.
    • That is, they come from different data generating processes.
  • It also states that smokers' babies weigh significantly less.
No description has been provided for this image

Choosing a test statistic¶

We need a test statistic that can measure how different two numerical distributions are.

In [57]:
px.histogram(baby, color='Maternal Smoker', histnorm='probability', marginal='box', 
             title="Birth Weight by Mother's Smoking Status", barmode='overlay', opacity=0.7)

Easiest solution: Difference in group means.

Difference in group means¶

We'll choose our test statistic to be:

$$\text{mean weight of smokers' babies} - \text{mean weight of non-smokers' babies}$$

We could also compute the non-smokers' mean minus the smokers' mean, too.

In [58]:
group_means = baby.groupby('Maternal Smoker')['Birth Weight'].mean()
group_means
Out[58]:
Maternal Smoker
False    123.09
True     113.82
Name: Birth Weight, dtype: float64

At first, you may think to use loc with group_means to compute the difference in group means.

In [59]:
group_means.loc[True] - group_means.loc[False]
Out[59]:
-9.266142572024918

However, you can also use the diff method.

In [60]:
pd.Series([1, 2, -3]).diff()
Out[60]:
0    NaN
1    1.0
2   -5.0
dtype: float64
In [61]:
group_means.diff()
Out[61]:
Maternal Smoker
False     NaN
True    -9.27
Name: Birth Weight, dtype: float64
In [62]:
group_means.diff().iloc[-1]
Out[62]:
-9.266142572024918
In [63]:
# If we wanted to do (non-smokers' mean - smokers' mean). 
# Think about why this is the case (hint: it has to do with how the resulting DataFrame after grouping is sorted).
group_means[::-1].diff().iloc[-1]
Out[63]:
9.266142572024918

Hypothesis test setup¶

  • Null Hypothesis: In the population, birth weights of smokers' babies and non-smokers' babies have the same distribution, and the observed differences in our samples are due to random chance.

  • Alternative Hypothesis: In the population, smokers' babies have lower birth weights than non-smokers' babies, on average. The observed difference in our samples cannot be explained by random chance alone.

  • Test Statistic: Difference in group means.

$$\text{mean weight of smokers' babies} - \text{mean weight of non-smokers' babies}$$
  • Issue: We don't know what the population distribution actually is – so how do we draw samples from it?
    • This is different from the coin flipping, and the California ethnicity examples, because there the null hypotheses were well-defined probability models.

Implications of the null hypothesis¶

  • Under the null hypothesis, both groups are sampled from the same distribution.
  • If this is true, then the group label – 'Maternal Smoker' – has no effect on the birth weight.
  • In our dataset, we saw one assignment of True or False to each baby.
In [64]:
baby.head()
Out[64]:
Maternal Smoker Birth Weight
0 False 120
1 False 113
2 True 128
3 True 108
4 False 136
  • Under the null hypothesis, we were just as likely to see any other assignment.

Permutation tests¶

  • In a permutation test, we generate new data by shuffling group labels.

    • In our current example, this involves randomly assigning babies to True or False, while keeping the same number of Trues and Falses as we started with.

  • On each shuffle, we'll compute our test statistic (difference in group means).

  • If we shuffle many times and compute our test statistic each time, we will approximate the distribution of the test statistic.

  • We can them compare our observed statistic to this distribution, as in any other hypothesis test.

Shuffling¶

  • Our goal, by shuffling, is to randomly assign values in the 'Maternal Smoker' column to values in the 'Birth Weight' column.

  • We can do this by shuffling either column independently.

  • Easiest solution: np.random.permutation.

    • Could also use df.sample, but it's more complicated.
In [65]:
np.random.permutation(baby['Birth Weight'])
Out[65]:
array([102, 133, 133, ..., 122,  96, 152])
In [67]:
with_shuffled = baby.assign(Shuffled_Weights=np.random.permutation(baby['Birth Weight']))
with_shuffled.head()
Out[67]:
Maternal Smoker Birth Weight Shuffled_Weights
0 False 120 115
1 False 113 62
2 True 128 132
3 True 108 105
4 False 136 107

  • Now, we have a new sample of smokers' weights, and a new sample of non-smokers' weights!

  • Effectively, we took a random sample of 459 'Birth Weights' and assigned them to the smokers' group, and the remaining 715 to the non-smokers' group.

How close are the means of the shuffled groups?¶

One benefit of shuffling 'Birth Weight' (instead of 'Maternal Smoker') is that grouping by 'Maternal Smoker' allows us to see all of the following information with a single call to groupby.

In [68]:
group_means = with_shuffled.groupby('Maternal Smoker').mean()
group_means
Out[68]:
Birth Weight Shuffled_Weights
Maternal Smoker
False 123.09 119.10
True 113.82 120.02

Let's visualize both pairs of distributions – what do you notice?

In [76]:
for x in ['Birth Weight', 'Shuffled_Weights']:
    fig = px.histogram(
        with_shuffled, x=x, color='Maternal Smoker', histnorm='probability', marginal='box', 
        title=f"Using the {x} column <br>(difference in means = {group_means[x].diff().iloc[-1]:.2f})",
        barmode='overlay', opacity=0.7)
    fig.update_layout(margin=dict(t=60))
    fig.show()

Simulating the empirical distribution of the test statistic¶

  • This was just one random shuffle.

  • The question we are trying to answer is, how likely is it that a random shuffle results in two samples where the smokers' mean is at least 9.26 ounces less than the non-smokers' mean?

  • To answer this question, we need the distribution of the test statistic. To generate that, we must shuffle many, many times. On each iteration, we must:

    1. Shuffle the weights and store them in a DataFrame.
    2. Compute the test statistic (difference in group means).
    3. Store the result.
In [80]:
n_repetitions = 500

differences = []
for _ in range(n_repetitions):
    
    # Step 1: Shuffle the weights and store them in a DataFrame.
    with_shuffled = baby.assign(Shuffled_Weights=np.random.permutation(baby['Birth Weight']))

    # Step 2: Compute the test statistic.
    # Remember, False (0) comes before True (1),
    # so this computes True - False.
    group_means = (
        with_shuffled
        .groupby('Maternal Smoker')
        .mean()
        .loc[:, 'Shuffled_Weights']
    )
    difference = group_means.diff().iloc[-1]
    
    # Step 4: Store the result
    differences.append(difference)
    
differences[:10]
Out[80]:
[0.8896719837896256,
 0.9755259990554066,
 -0.23000746530158267,
 -0.4732605085546169,
 1.5299998476469057,
 -0.015372427137137379,
 -0.4517970047381823,
 0.9969895028718554,
 0.3530843883785053,
 -0.3874064932888359]

We already computed the observed statistic earlier, but we compute it again below to keep all of our calculations together.

In [81]:
observed_difference = baby.groupby('Maternal Smoker')['Birth Weight'].mean().diff().iloc[-1]
observed_difference
Out[81]:
-9.266142572024918

Conclusion of the test¶

In [86]:
fig = px.histogram(
    pd.DataFrame(differences), x=0, nbins=50, histnorm='probability', 
    title='Empirical Distribution of the Mean Differences <br> in Birth Weights (Smoker - Non-Smoker)')
fig.add_vline(x=observed_difference, line_color='red')
fig.update_layout(xaxis_range=[-10, 10], margin=dict(t=60))

  • Under the null hypothesis, we rarely see differences as large as 9.26 ounces.

  • Therefore, we reject the null hypothesis that the two groups come from the same distribution.

⚠️ Caution!¶

  • We cannot conclude that smoking causes lower birth weight!
  • This was an observational study; there may be confounding factors.
    • Maybe smokers are more likely to drink caffeine, and caffeine causes lower birth weight.

Differences between categorical distributions¶

Example: Married vs. unmarried couples¶

  • We will use data from a study conducted in 2010 by the National Center for Family and Marriage Research.
  • The data consists of a national random sample of over 1,000 heterosexual couples who were either married or living together but unmarried.
  • Each row corresponds to one person (not one couple).
In [89]:
couples = pd.read_csv('data/married_couples.csv')
couples.head()
Out[89]:
hh_id gender mar_status rel_rating ... education hh_income empl_status hh_internet
0 0 1 1 1 ... 12 14 1 1
1 0 2 1 1 ... 9 14 1 1
2 1 1 1 1 ... 11 15 1 1
3 1 2 1 1 ... 9 15 1 1
4 2 1 1 1 ... 12 14 1 1

5 rows × 9 columns

In [90]:
# What does this expression compute?
couples['hh_id'].value_counts().value_counts()
Out[90]:
2    1033
1       2
Name: hh_id, dtype: int64

We won't use all of the columns in the DataFrame.

In [91]:
couples = couples[['mar_status', 'empl_status', 'gender', 'age']]
couples.head()
Out[91]:
mar_status empl_status gender age
0 1 1 1 51
1 1 1 2 53
2 1 1 1 57
3 1 1 2 57
4 1 1 1 60

Cleaning the dataset¶

The numbers in the DataFrame correspond to the mappings below.

  • 'mar_status': 1=married, 2=unmarried.
  • 'empl_status': enumerated in the list below.
  • 'gender': 1=male, 2=female.
  • 'age': person's age in years.
In [92]:
couples.head()
Out[92]:
mar_status empl_status gender age
0 1 1 1 51
1 1 1 2 53
2 1 1 1 57
3 1 1 2 57
4 1 1 1 60
In [93]:
empl = [
    'Working as paid employee',
    'Working, self-employed',
    'Not working - on a temporary layoff from a job',
    'Not working - looking for work',
    'Not working - retired',
    'Not working - disabled',
    'Not working - other'
]
In [94]:
couples = couples.replace({
    'mar_status': {1: 'married', 2: 'unmarried'},
    'gender': {1: 'M', 2: 'F'},
    'empl_status': {(k + 1): empl[k] for k in range(len(empl))}
})
In [95]:
couples.head()
Out[95]:
mar_status empl_status gender age
0 married Working as paid employee M 51
1 married Working as paid employee F 53
2 married Working as paid employee M 57
3 married Working as paid employee F 57
4 married Working as paid employee M 60

Understanding the couples dataset¶

  • Who is in our dataset? Mostly young people? Mostly married people? Mostly employed people?
  • What is the distribution of values in each column?
In [96]:
# For categorical columns, this shows the 10 most common values and their frequencies.
# For numerical columns, this shows the result of calling the .describe() method.
for col in couples:
    if couples[col].dtype == 'object':
        empr = couples[col].value_counts(normalize=True).to_frame().iloc[:10]
    else:
        empr = couples[col].describe().to_frame()
    display(empr)
mar_status
married 0.72
unmarried 0.28
empl_status
Working as paid employee 0.61
Not working - other 0.10
Working, self-employed 0.10
Not working - looking for work 0.07
Not working - disabled 0.06
Not working - retired 0.05
Not working - on a temporary layoff from a job 0.02
gender
M 0.5
F 0.5
age
count 2068.00
mean 43.17
std 11.91
... ...
50% 44.00
75% 53.00
max 64.00

8 rows × 1 columns

Let's look at the distribution of age separately for married couples and unmarried couples.

In [97]:
px.histogram(couples, x='age', color='mar_status', histnorm='probability', marginal='box',
             barmode='overlay', opacity=0.7)

How are these two distributions different? Why do you think there is a difference?

Understanding employment status in households¶

  • Do married households more often have a stay-at-home spouse?
  • Do households with unmarried couples more often have someone looking for work?
  • How much does the employment status of the different households vary?

To answer these questions, let's compute the distribution of employment status conditional on household type (married vs. unmarried).

In [98]:
couples.sample(5).head()
Out[98]:
mar_status empl_status gender age
1497 unmarried Working as paid employee F 30
1488 married Working as paid employee M 42
1080 married Working as paid employee M 61
467 married Working as paid employee F 54
1179 married Not working - other F 30
In [99]:
# Note that this is a shortcut to picking a column for values and using aggfunc='count'.
empl_cnts = couples.pivot_table(index='empl_status', columns='mar_status', aggfunc='size')
empl_cnts
Out[99]:
mar_status married unmarried
empl_status
Not working - disabled 72 45
Not working - looking for work 71 69
Not working - on a temporary layoff from a job 21 13
Not working - other 182 33
Not working - retired 94 11
Working as paid employee 906 347
Working, self-employed 138 66

Since there are a different number of married and unmarried couples in the dataset, we can't compare the numbers above directly. We need to convert counts to proportions, separately for married and unmarried couples.

In [100]:
empl_cnts.sum()
Out[100]:
mar_status
married      1484
unmarried     584
dtype: int64
In [101]:
cond_distr = empl_cnts / empl_cnts.sum()
cond_distr
Out[101]:
mar_status married unmarried
empl_status
Not working - disabled 0.05 0.08
Not working - looking for work 0.05 0.12
Not working - on a temporary layoff from a job 0.01 0.02
Not working - other 0.12 0.06
Not working - retired 0.06 0.02
Working as paid employee 0.61 0.59
Working, self-employed 0.09 0.11

Both of the columns above sum to 1.

Differences in the distributions¶

Are the distributions of employment status for married people and for unmarried people who live with their partners different?

Is this difference just due to noise?

In [102]:
cond_distr.plot(kind='barh', title='Distribution of Employment Status, Conditional on Household Type', barmode='group')

Permutation test for household composition¶

  • Null Hypothesis: In the US, the distribution of employment status among those who are married is the same as among those who are unmarried and live with their partners. The difference between the two observed samples is due to chance.

  • Alternative Hypothesis: In the US, the distributions of employment status of the two groups are different.

Discussion Question¶

What is a good test statistic in this case?

*Hint:* What kind of distributions are we comparing?

Total variation distance¶

  • Whenever we need to compare two categorical distributions, we use the TVD.
    • Recall, the TVD is the sum of the absolute differences in proportions, divided by 2.
  • In DSC 10, the only test statistic we ever used in permutation tests was the difference in group means/medians, but the TVD can be used in permutation tests as well.
In [103]:
cond_distr
Out[103]:
mar_status married unmarried
empl_status
Not working - disabled 0.05 0.08
Not working - looking for work 0.05 0.12
Not working - on a temporary layoff from a job 0.01 0.02
Not working - other 0.12 0.06
Not working - retired 0.06 0.02
Working as paid employee 0.61 0.59
Working, self-employed 0.09 0.11

Let's first compute the observed TVD:

In [108]:
(cond_distr['unmarried'] - cond_distr['married']).abs().sum() / 2
Out[108]:
0.1269754089281099

Since we'll need to calculate the TVD repeatedly, let's define a function that computes it.

In [109]:
def tvd_of_groups(df, groups, cats):
    '''groups: the binary column (e.g. married vs. unmarried).
       cats: the categorical column (e.g. employment status).
    '''
    cnts = df.pivot_table(index=cats, columns=groups, aggfunc='size')
    # Normalize each column.
    distr = cnts / cnts.sum()
    # Compute and return the TVD.
    return (distr['unmarried'] - distr['married']).abs().sum() / 2
In [110]:
# Same result as above.
observed_tvd = tvd_of_groups(couples, groups='mar_status', cats='empl_status')
observed_tvd
Out[110]:
0.1269754089281099

Simulation¶

  • Under the null hypothesis, marital status is not related to employment status.
  • We can shuffle the marital status column and get an equally-likely dataset.
  • On each shuffle, we will compute the TVD.
  • Once we have many TVDs, we can ask, how often do we see a difference at least as large as our observed difference?
In [111]:
couples.head()
Out[111]:
mar_status empl_status gender age
0 married Working as paid employee M 51
1 married Working as paid employee F 53
2 married Working as paid employee M 57
3 married Working as paid employee F 57
4 married Working as paid employee M 60

Here, we'll shuffle marital statuses, though remember, we could shuffle employment statuses too.

In [112]:
couples.assign(shuffled_mar=np.random.permutation(couples['mar_status']))
Out[112]:
mar_status empl_status gender age shuffled_mar
0 married Working as paid employee M 51 married
1 married Working as paid employee F 53 unmarried
2 married Working as paid employee M 57 unmarried
... ... ... ... ... ...
2065 unmarried Working as paid employee F 53 unmarried
2066 unmarried Working as paid employee M 44 unmarried
2067 unmarried Working as paid employee F 42 married

2068 rows × 5 columns

Let's do this repeatedly.

In [113]:
N = 1000
tvds = []

for _ in range(N):
    # Shuffle marital statuses.
    with_shuffled = couples.assign(shuffled_mar=np.random.permutation(couples['mar_status']))
    
    # Compute and store the TVD.
    tvd = tvd_of_groups(with_shuffled, groups='shuffled_mar', cats='empl_status')
    tvds.append(tvd)

Notice that by defining a function that computes our test statistic, our simulation code is much cleaner.

Conclusion of the test¶

In [121]:
fig = px.histogram(tvds, x=0, nbins=50, histnorm='probability', 
                   title='Empirical Distribution of the TVD')
fig.update_layout(xaxis_range=[0, 0.2])

We reject the null hypothesis that married/unmarried households have similar employment makeups.

We can't say anything about why the employment makeups are different, though!

In our Framework¶

No description has been provided for this image No description has been provided for this image

Discussion Question¶

In the definition of the TVD, we divide the sum of the absolute differences in proportions between the two distributions by 2.

def tvd(a, b):
    return np.sum(np.abs(a - b)) / 2

Question: If we divided by 200 instead of 2, would we still reject the null hypothesis?

Student-Submitted Questions¶

  • Come up with a question or two that could be answered with a hypothesis test.
    • E.g. Is it faster to take the stairs or elevator up to the third floor of HDSI?
  • I will explain the data we would gather and the hypothesis test we would run!
  • Will go until no more questions or we run out of time.
  • https://wall.sli.do/event/g2dESFa2co9kwmUwqfuCNL?section=e82e38eb-254e-4eb9-9de3-341347c52119