In [1]:
from dsc80_utils import *
In [2]:
import lec08_utils as util

Lecture 8 – Imputation¶

DSC 80, Fall 2023¶

📣 Announcements 📣¶

  • Good job on Project 2 checkpoint!
  • Lab 4 due Monday.
  • Midterm exam will happen next week on Thurs Nov 2.

📝 Midterm Exam¶

  • Thurs, Nov 2 from 3:30-4:50pm in WLH 2005.
  • Pen and paper only. No calculators, phones, or watches allowed.
  • You are allowed to bring one double-sided 8.5" x 11" sheet of handwritten notes.
    • No reference sheet given, unlike DSC 10!
  • We will display clarifications and the time remaining during the exam.
  • Covers Lectures 1-8, Labs 1-4, and Projects 1-2.
  • To review problems from old exams, go to practice.dsc80.com.
    • Also look at the Resources tab on the course website.

📆 Agenda¶

  • Review of missingness mechanisms
  • Deciding between MCAR and MAR using a hypothesis test
    • The Kolmogorov-Smirnov test statistic
  • Mean Imputation
  • Probabilistic Imputation
  • Multiple Imputation

Review: Missingness mechanisms¶

A good strategy is to assess missingness in the following order.

Missing by design (MD)
Can I determine the missing value exactly by looking at the other columns? 🤔
⬇️
Not missing at random (NMAR)
Is there a good reason why the missingness depends on the values themselves? 🤔
⬇️
Missing at random (MAR)
Do other columns tell me anything about the likelihood that a value is missing? 🤔
⬇️
Missing completely at random (MCAR)
The missingness must not depend on other columns or the values themselves. 😄

Review: Assessing missingness through data¶

Example: Heights¶

  • Let's load in Galton's dataset containing the heights of adult children and their parents (which you may have seen in DSC 10).
  • The dataset does not contain any missing values – we will artifically introduce missing values such that the values are MCAR, for illustration.
In [3]:
heights = pd.read_csv('data/midparent.csv')
heights = heights.rename(columns={'childHeight': 'child'})
heights = heights[['father', 'mother', 'gender', 'child']]
heights.head()
Out[3]:
father mother gender child
0 78.5 67.0 male 73.2
1 78.5 67.0 female 69.2
2 78.5 67.0 female 69.0
3 78.5 67.0 female 69.0
4 75.5 66.5 male 73.5

Simulating MCAR data¶

  • We will make 'child' MCAR by taking a random subset of heights and setting the corresponding 'child' heights to np.NaN.
  • This is equivalent to flipping a (biased) coin for each row.
    • If heads, we delete the 'child' height.
  • You will not do this in practice!
In [4]:
np.random.seed(42) # So that we get the same results each time (for lecture).

heights_mcar = heights.copy()
idx = heights_mcar.sample(frac=0.3).index
heights_mcar.loc[idx, 'child'] = np.NaN
In [5]:
heights_mcar.head(10)
Out[5]:
father mother gender child
0 78.5 67.0 male 73.2
1 78.5 67.0 female 69.2
2 78.5 67.0 female NaN
... ... ... ... ...
7 75.5 66.5 female NaN
8 75.0 64.0 male 71.0
9 75.0 64.0 female 68.0

10 rows × 4 columns

In [6]:
heights_mcar.isna().mean()
Out[6]:
father    0.0
mother    0.0
gender    0.0
child     0.3
dtype: float64

Aside: Why is the value for 'child' in the above Series not exactly 0.3?

Verifying that child heights are MCAR in heights_mcar¶

  • Each row of heights_mcar belongs to one of two groups:
    • Group 1: 'child' is missing.
    • Group 2: 'child' is not missing.
In [7]:
heights_mcar['child_missing'] = heights_mcar['child'].isna()
heights_mcar.head()
Out[7]:
father mother gender child child_missing
0 78.5 67.0 male 73.2 False
1 78.5 67.0 female 69.2 False
2 78.5 67.0 female NaN True
3 78.5 67.0 female 69.0 False
4 75.5 66.5 male 73.5 False
  • We need to look at the distributions of every other column – 'gender', 'mother', and 'father' – separately for these two groups, and check to see if they are similar.

Comparing null and non-null 'child' distributions for 'gender'¶

In [8]:
gender_dist = (
    heights_mcar
    .assign(child_missing=heights_mcar['child'].isna())
    .pivot_table(index='gender', columns='child_missing', aggfunc='size')
)

# Added just to make the resulting pivot table easier to read.
gender_dist.columns = ['child_missing = False', 'child_missing = True']

gender_dist = gender_dist / gender_dist.sum()
gender_dist
Out[8]:
child_missing = False child_missing = True
gender
female 0.49 0.48
male 0.51 0.52

  • Note that here, each column is a separate distribution that adds to 1.

  • The two columns look similar, which is evidence that 'child''s missingness does not depend on 'gender'.

    • Knowing that the child is 'female' doesn't make it any more or less likely that their height is missing than knowing if the child is 'male'.

Comparing null and non-null 'child' distributions for 'gender'¶

  • In the previous slide, we saw that the distribution of 'gender' is similar whether or not 'child' is missing.

  • To make precise what we mean by "similar", we can run a permutation test. We are comparing two distributions:

    1. The distribution of 'gender' when 'child' is missing.
    2. The distribution of 'gender' when 'child' is not missing.

  • What test statistic do we use to compare categorical distributions?

In [9]:
gender_dist.plot(kind='barh', title='Gender by Missingness of Child Height', barmode='group')

To measure the "distance" between two categorical distributions, we use the total variation distance.

Note that with only two categories, the TVD is the same as the absolute difference in proportions for either category.

Simulation¶

The code to run our simulation largely looks the same as in previous permutation tests.

In [10]:
n_repetitions = 500
shuffled = heights_mcar.copy()

tvds = []
for _ in range(n_repetitions):
    
    # Shuffling genders. 
    # Note that we are assigning back to the same DataFrame for performance reasons; 
    # see https://dsc80.com/resources/lectures/lec07/lec07-fast-permutation-tests.html
    shuffled['gender'] = np.random.permutation(shuffled['gender'])
    
    # Computing and storing the TVD.
    pivoted = (
        shuffled
        .pivot_table(index='gender', columns='child_missing', aggfunc='size')
        .apply(lambda x: x / x.sum())
    )
    
    tvd = pivoted.diff(axis=1).iloc[:, -1].abs().sum() / 2
    tvds.append(tvd)
In [11]:
observed_tvd = gender_dist.diff(axis=1).iloc[:, -1].abs().sum() / 2
observed_tvd
Out[11]:
0.009196155526430771

Results¶

In [ ]:
In [12]:
fig = px.histogram(pd.DataFrame(tvds), x=0, nbins=50, histnorm='probability', 
                   title='Empirical Distribution of the TVD')
fig.add_vline(x=observed_tvd, line_color='red', line_width=2, opacity=1)
fig.add_annotation(text=f'<span style="color:red">Observed TVD = {round(observed_tvd, 2)}</span>',
                   x=4 * observed_tvd, showarrow=False, y=0.16)
fig.update_layout(yaxis_range=[0, 0.2])
In [13]:
np.mean(np.array(tvds) >= observed_tvd)
Out[13]:
0.838
  • We fail to reject the null.
  • Recall, the null stated that the distribution of 'gender' when 'child' is missing is the same as the distribution of 'gender' when 'child' is not missing.
  • Hence, we conclude that the missingness in the 'child' column is not dependent on 'gender'.

Comparing null and non-null 'child' distributions for 'father'¶

  • We again must compare two distributions:

    1. The distribution of 'father' when 'child' is missing.
    2. The distribution of 'father' when 'child' is not missing.

  • If the distributions are similar, we conclude that the missingness of 'child' is not dependent on the height of the 'father'.

  • We can again use a permutation test.

In [14]:
px.histogram(heights_mcar, x='father', color='child_missing', histnorm='probability', marginal='box',
             title="Father's Height by Missingness of Child Height", barmode='overlay', opacity=0.7)

We can visualize numerical distributions with histograms, or with kernel density estimates. (See the definition of create_kde_plotly at the top of the notebook if you're curious as to how these are created.)

In [15]:
util.create_kde_plotly(heights_mcar, 'child_missing', True, False, 'father', 
                       "Father's Height by Missingness of Child Height")

Concluding that 'child' is MCAR¶

  • We need to run three permutation tests – one for each column in heights_mcar other than 'child'.

  • For every other column, if we fail to reject the null that the distribution of the column when 'child' is missing is the same as the distribution of the column when 'child' is not missing, then we can conclude 'child' is MCAR.

    • In such a case, its missingness is not tied to any other columns.
    • For instance, children with shorter fathers are not any more likely to have missing heights than children with taller fathers.

Simulating MAR data¶

Now, we will make 'child' heights MAR by deleting 'child' heights according to a random procedure that depends on other columns.

In [16]:
np.random.seed(42) # So that we get the same results each time (for lecture).

def make_missing(r):
    rand = np.random.uniform() # Random real number between 0 and 1.
    if r['father'] > 72 and rand < 0.5:
        return np.NaN
    elif r['gender'] == 'female' and rand < 0.3:
        return np.NaN
    else:
        return r['child']
    
heights_mar = heights.copy()
heights_mar['child'] = heights_mar.apply(make_missing, axis=1)
heights_mar['child_missing'] = heights_mar['child'].isna()
In [17]:
heights_mar.head()
Out[17]:
father mother gender child child_missing
0 78.5 67.0 male NaN True
1 78.5 67.0 female 69.2 False
2 78.5 67.0 female 69.0 False
3 78.5 67.0 female 69.0 False
4 75.5 66.5 male NaN True

Comparing null and non-null 'child' distributions for 'gender', again¶

This time, the distribution of 'gender' in the two groups is very different.

In [18]:
gender_dist = (
    heights_mar
    .assign(child_missing=heights_mar['child'].isna())
    .pivot_table(index='gender', columns='child_missing', aggfunc='size')
)

# Added just to make the resulting pivot table easier to read.
gender_dist.columns = ['child_missing = False', 'child_missing = True']

gender_dist = gender_dist / gender_dist.sum()
gender_dist
Out[18]:
child_missing = False child_missing = True
gender
female 0.4 0.88
male 0.6 0.12
In [19]:
gender_dist.plot(kind='barh', title='Gender by Missingness of Child Height', barmode='group')

Comparing null and non-null 'child' distributions for 'father', again¶

In [20]:
util.create_kde_plotly(heights_mar, 'child_missing', True, False, 'father', 
                       "Father's Height by Missingness of Child Height")

  • The above two distributions look quite different.

    • This is because we artificially created missingness in the dataset in a way that depended on 'father' and 'gender'.

  • However, their difference in means is small:

In [21]:
heights_mar.groupby('child_missing')['father'].mean().diff().iloc[-1]
Out[21]:
1.0055466604787853
  • If we ran a permutation test with the difference in means as our test statistic, we would fail to reject the null.
    • Using just the difference in means, it is hard to tell these two distributions apart.

The Kolmogorov-Smirnov test statistic¶

Recap: Permutation tests¶

  • Permutation tests help decide whether two samples look like they were drawn from the same population distribution.
  • In a permutation test, we simulate data under the null by shuffling either group labels or numerical features.
    • In effect, this randomly assigns individuals to groups.
  • If the two distributions are quantitative (numerical), we've used as our test statistic the difference in group means or medians.
  • If the two distributions are qualitative (categorical), we've used as our test statistic the total variation distance (TVD).

Difference in means¶

The difference in means works well in some cases. Let's look at one such case.

Below, we artificially generate two numerical datasets.

In [22]:
np.random.seed(42) # So that we get the same results each time (for lecture).

N = 1000 # Number of samples for each distribution.

# Distribution 'A'.
distr1 = pd.Series(np.random.normal(0, 1, size=N//2))

# Distribution 'B'.
distr2 = pd.Series(np.random.normal(3, 1, size=N//2))

data = pd.concat([distr1, distr2], axis=1, keys=['A', 'B']).unstack().reset_index().drop('level_1', axis=1)
data = data.rename(columns={'level_0': 'group', 0: 'data'})

meanA, meanB = data.groupby('group')['data'].mean().round(7).tolist()
util.create_kde_plotly(data, 'group', 'A', 'B', 'data', f'mean of A: {meanA}<br>mean of B: {meanB}')

Discussion Question¶

  • So far, we have used the difference in means as our test statistic in quantitative permutation tests.
  • We've concluded that two distributions were likely different if their means were different.
  • Can you think of two different distributions that have the same mean? 🤔

Different distributions with the same mean¶

Let's generate two distributions that look very different but have the same mean.

In [23]:
np.random.seed(42) # So that we get the same results each time (for lecture).

N = 1000 # Number of samples for each distribution.

# Distribution 'A'.
a = pd.Series(np.random.normal(0, 1, size=N//2))
b = pd.Series(np.random.normal(4, 1, size=N//2))
distr1 = pd.concat([a,b], ignore_index=True)

# Distribution 'B'.
distr2 = pd.Series(np.random.normal(distr1.mean(), distr1.std(), size=N))

data = pd.concat([distr1, distr2], axis=1, keys=['A', 'B']).unstack().reset_index().drop('level_1', axis=1)
data = data.rename(columns={'level_0': 'group', 0: 'data'})

meanA, meanB = data.groupby('group')['data'].mean().round(7).tolist()
util.create_kde_plotly(data, 'group', 'A', 'B', 'data', f'mean of A: {meanA}<br>mean of B: {meanB}')

In this case, if we use the difference in means as our test statistic in a permutation test, we will fail to reject the null that the two distributions are different.

In [24]:
n_repetitions = 500
shuffled = data.copy()

diff_means = []
for _ in range(n_repetitions):
    
    # Shuffling the values, while keeping the group labels in place.
    shuffled['data'] = np.random.permutation(shuffled['data'])
    
    # Computing and storing the absolute difference in means.
    diff_mean = shuffled.groupby('group')['data'].mean().diff().abs().iloc[-1]
    diff_means.append(diff_mean)
In [25]:
observed_diff = data.groupby('group')['data'].mean().diff().abs().iloc[-1]
fig = px.histogram(pd.DataFrame(diff_means), x=0, nbins=50, histnorm='probability', 
                   title='Empirical Distribution of the Absolute Difference in Means')
fig.add_vline(x=observed_diff, line_color='red', line_width=1, opacity=1)
fig.add_annotation(text=f'<span style="color:red">Observed Absolute Difference in Means = {round(observed_diff, 2)}</span>',
                   x=1.45 * observed_diff, showarrow=False, y=0.07)
In [26]:
# The computed p-value is fairly large.
np.mean(np.array(diff_means) >= observed_diff)
Out[26]:
0.108

Telling quantitative distributions apart¶

  • The difference in means only works as a test statistic in permutation tests if the two distributions have similar shapes.

    • It tests to see if one is a shifted version of the other.

  • We need a better test statistic to differentiate between quantitative distributions with different shapes.

  • In other words, we need a distance metric between quantitative distributions.

    • The TVD is a distance metric between categorical distributions.
In [27]:
util.create_kde_plotly(data, 'group', 'A', 'B', 'data', f'mean of A: {meanA}<br>mean of B: {meanB}')

The Kolmogorov-Smirnov test statistic¶

  • The K-S test statistic measures the similarity between two distributions.
  • It is defined in terms of the cumulative distribution function (CDF) of a given distribution.
    • If $f(x)$ is a distribution, then the CDF $F(x)$ is the proportion of values in distribution $f$ that are less than or equal to $x$.
  • The K-S statistic is roughly defined as the largest difference between two CDFs.
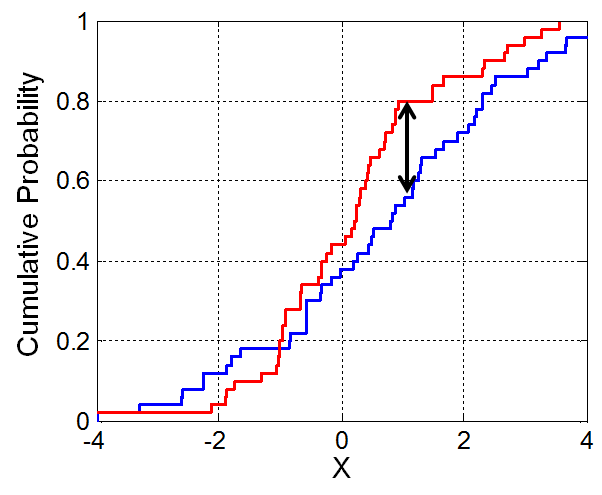
No description has been provided for this image

Aside: cumulative distribution functions¶

Let's look at the CDFs of our two synthetic distributions.

In [28]:
# Think about what this function is doing!
def create_cdf(group):
    return data.loc[data['group'] == group, 'data'].value_counts(normalize=True).sort_index().cumsum()

fig = go.Figure()

fig.add_trace(
    go.Scatter(x=create_cdf('A').index, y=create_cdf('A'), name='CDF of A')
)

fig.add_trace(
    go.Scatter(x=create_cdf('B').index, y=create_cdf('B'), name='CDF of B')
)

fig.update_layout(title='CDFs of A and B')

The K-S statistic in Python¶

Fortunately, we don't need to calculate the K-S statistic ourselves! Python can do it for us (and you can use this pre-built version in all assignments).

In [29]:
from scipy.stats import ks_2samp
In [30]:
ks_2samp?
In [31]:
observed_ks = ks_2samp(data.loc[data['group'] == 'A', 'data'], data.loc[data['group'] == 'B', 'data']).statistic
observed_ks
Out[31]:
0.14

We don't know if this number is big or small. We need to run a permutation test!

In [32]:
n_repetitions = 500
shuffled = data.copy()

ks_stats = []
for _ in range(n_repetitions):
    
    # Shuffling the data.
    shuffled['data'] = np.random.permutation(shuffled['data'])
    
    # Computing and storing the K-S statistic.
    groups = shuffled.groupby('group')['data']
    ks_stat = ks_2samp(groups.get_group('A'), groups.get_group('B')).statistic
    ks_stats.append(ks_stat)
    
ks_stats[:10]
Out[32]:
[0.037, 0.048, 0.04, 0.068, 0.045, 0.04, 0.042, 0.052, 0.019, 0.029]
In [33]:
fig = px.histogram(pd.DataFrame(ks_stats), x=0, nbins=50, histnorm='probability', 
                   title='Empirical Distribution of the K-S Statistic')
fig.add_vline(x=observed_ks, line_color='red', line_width=1, opacity=1)
fig.add_annotation(text=f'<span style="color:red">Observed KS = {round(observed_ks, 2)}</span>',
                   x=0.8 * observed_ks, showarrow=False, y=0.16)

fig.update_layout(xaxis_range=[0, 0.2])
fig.update_layout(yaxis_range=[0, 0.2])
In [34]:
np.mean(np.array(ks_stats) >= observed_ks)
Out[34]:
0.0

We were able to differentiate between the two distributions using the K-S test statistic!

ks_2samp¶

  • scipy.stats.ks_2samp actually returns both the statistic and a p-value.
  • The p-value is calculated using the permutation test we just performed!
In [35]:
ks_2samp(data.loc[data['group'] == 'A', 'data'], data.loc[data['group'] == 'B', 'data'])
Out[35]:
KstestResult(statistic=0.14, pvalue=5.822752148022591e-09, statistic_location=0.9755451271223592, statistic_sign=1)

Difference in means vs. K-S statistic¶

  • The K-S statistic measures the difference between two numeric distributions.

  • It does not quantify if one is larger than the other on average, so there are times we still need to use the difference in means.

  • Strategy: Always plot the two distributions you are comparing.

    • If the distributions have similar shapes but are centered in different places, use the difference in means (or absolute difference in means).
    • If your alternative hypothesis involves a "direction" (i.e. smoking weights were are on average than non-smoking weights), use the difference in means.
    • If the distributions have different shapes and your alternative hypothesis is simply that the two distributions are different, use the K-S statistic.

Back to our Example: Missingness of 'child' heights on 'father''s heights (MAR)¶

  • Question: Is the missingness of 'child' heights dependent on the 'father' column?

  • We will follow the same procedure as before. The only difference is that the missing values in our simulated data are MAR dependent on 'father'.

In [36]:
# Our MAR data
heights_mar.isna().mean()
Out[36]:
father           0.00
mother           0.00
gender           0.00
child            0.18
child_missing    0.00
dtype: float64

Example: Missingness of 'child' heights on 'father''s heights (MAR)¶

In [37]:
heights_mar['child_missing'] = heights_mar['child'].isna()
util.create_kde_plotly(heights_mar[['child_missing', 'father']], 'child_missing', True, False, 'father',
                       "Father's Height by Missingness of Child Height (MAR example)")

  • The above picture shows us that missing 'child' heights tend to come from taller 'father's heights.

  • To determine whether the two distributions are significantly different, we must use a permutation test. This time, the difference in means is not a good choice, since the centers are similar but the shapes are different.

Discussion Question¶

In this MAR example, if we were to take the mean of the 'child' column that contains missing values, is the result likely to:

  1. Overestimate the true mean?
  2. Underestimate the true mean?
  3. Be accurate?
In [38]:
util.create_kde_plotly(heights_mar[['child_missing', 'father']], 'child_missing', True, False, 'father',
                       "Father's Height by Missingness of Child Height (MAR example)")

Performing the test¶

In [39]:
heights_mar
Out[39]:
father mother gender child child_missing
0 78.5 67.0 male NaN True
1 78.5 67.0 female 69.2 False
2 78.5 67.0 female 69.0 False
... ... ... ... ... ...
931 62.0 66.0 female 61.0 False
932 62.5 63.0 male 66.5 False
933 62.5 63.0 female 57.0 False

934 rows × 5 columns

In [40]:
ks_2samp(heights_mar.query('child_missing')['father'], heights_mar.query('not child_missing')['father'])
Out[40]:
KstestResult(statistic=0.20676025834396874, pvalue=1.1424922868036869e-05, statistic_location=72.0, statistic_sign=-1)

The p-value is very small, so we conclude that the child height is MAR, conditional on the father's height.

Handling missing values¶

What do we do with missing data?¶

  • Suppose we are interested in a dataset $Y$.
  • We get to observe $Y_{obs}$, while the rest of the dataset, $Y_{mis}$, is missing.
  • Issue: $Y_{obs}$ may look quite different than $Y$.
    • The mean and other measures of central tendency may be different.
    • The variance may be different.
    • The correlations between variables may be different.

Solution 1: Dropping missing values¶

  • If the data are MCAR (missing completely at random), then dropping the missing values entirely doesn't significantly change the data.

    • For instance, the mean of the dataset post-dropping is an unbiased estimate of the true mean.
    • This is because MCAR data is a random sample of the full dataset.
    • From DSC 10, we know that random samples tend to resemble the larger populations they are drawn from.

  • If the data are not MCAR, then dropping the missing values will introduce bias.

    • MCAR is rare!
    • For instance, suppose we asked people "How much do you give to charity?" People who give little are less likely to respond, so the average response is biased high.

Listwise deletion¶

  • Listwise deletion is the act of dropping entire rows that contain missing values.
  • Issue: This can delete perfectly good data in other columns for a given row.
    • Improvement: Drop missing data only when working with the column that contains missing data.

To illustrate, let's generate two datasets with missing 'child' heights – one in which the heights are MCAR, and one in which they are MAR dependent on 'gender' (not 'father', as in our previous example).

In practice, you'll have to run permutation tests to determine the likely missingness mechanism first!

In [41]:
np.random.seed(42) # So that we get the same results each time (for lecture).
heights_mcar = util.make_mcar(heights, 'child', pct=0.5)
heights_mar = util.make_mar_on_cat(heights, 'child', 'gender', pct=0.5)

Listwise deletion¶

Below, we compute the means and standard deviations of the 'child' column in all three datasets. Remember, .mean() and .std() ignore missing values.

In [42]:
util.multiple_describe({
    'Original': heights,
    'MCAR': heights_mcar,
    'MAR': heights_mar
})
Out[42]:
Mean Standard Deviation
Dataset
Original 66.75 3.58
MCAR 66.64 3.56
MAR 68.52 3.12

Observations:

  • The 'child' mean (and SD) in the MCAR dataset is very close to the true 'child' mean (and SD).

  • The 'child' mean in the MAR dataset is biased high.

Solution 2: Imputation¶

Imputation is the act of filling in missing data with plausable values. Ideally, imputation:

  • is quick and easy to do.
  • shouldn't introduce bias into the dataset.

These are hard to do at the same time!

Kinds of imputation¶

  • There are three main types of imputation, two of which we will focus on today:

    • Imputation with a single value: mean, median, mode.
    • Imputation with a single value, using a model: regression, kNN.
    • Probabilistic imputation by drawing from a distribution.

  • Each has upsides and downsides, and each works differently with different types of missingness.

Mean imputation¶

Mean imputation¶

  • Mean imputation is the act of filling in missing values in a column with the mean of the observed values in that column.
  • This strategy:
    • 👍 Preserves the mean of the observed data, for all types of missingness.
    • 👎 Decreases the variance of the data, for all types of missingness.
    • 👎 Creates a biased estimate of the true mean when the data are not MCAR.

Example: Mean imputation in the MCAR heights dataset¶

Let's look at two distributions:

  • The distribution of the 'child' column in heights, where we have all the data.
  • The distribution of the 'child' column in heights_mcar, where some values are MCAR.
In [43]:
# Look in util.py to see how multiple_kdes is defined.
util.multiple_kdes({'Original': heights, 'MCAR, Unfilled': heights_mcar})
  • Since the 'child' heights are MCAR, the orange distribution, in which some values are missing, has roughly the same shape as the turquoise distribution, which has no missing values.

Mean imputation of MCAR data¶

Let's fill in missing values in heights_mcar['child'] with the mean of the observed 'child' heights in heights_mcar['child'].

In [44]:
heights_mcar['child'].head()
Out[44]:
0    73.2
1    69.2
2     NaN
3     NaN
4    73.5
Name: child, dtype: float64
In [45]:
heights_mcar_mfilled = heights_mcar.fillna(heights_mcar['child'].mean())
heights_mcar_mfilled['child'].head()
Out[45]:
0    73.20
1    69.20
2    66.64
3    66.64
4    73.50
Name: child, dtype: float64
In [46]:
df_map = {'Original': heights, 'MCAR, Unfilled': heights_mcar, 'MCAR, Mean Imputed': heights_mcar_mfilled}
util.multiple_describe(df_map)
Out[46]:
Mean Standard Deviation
Dataset
Original 66.75 3.58
MCAR, Unfilled 66.64 3.56
MCAR, Mean Imputed 66.64 2.52

Observations:

  • The mean of the imputed dataset is the same as the mean of the subset of heights that aren't missing (which is close to the true mean).

  • The standard deviation of the imputed dataset smaller than that of the other two datasets. Why?

Mean imputation of MCAR data¶

Let's visualize all three distributions: the original, the MCAR heights with missing values, and the mean-imputed MCAR heights.

In [47]:
util.multiple_kdes(df_map)

Takeaway: When data are MCAR and you impute with the mean:

  • The mean of the imputed dataset is an unbiased estimator of the true mean.
  • The variance of the imputed dataset is smaller than the variance of the full dataset.
    • Mean imputation tricks you into thinking your data are more reliable than they are!

Example: Mean imputation in the MAR heights dataset¶

  • When data are MAR, mean imputation leads to biased estimates of the mean across groups.

  • The bias may be different in different groups.

    • For example: If the missingness depends on gender, then different genders will have differently-biased means.
    • The overall mean will be biased towards one group.

  • Again, let's look at two distributions:

    • The distribution of the 'child' column in heights, where we have all the data.
    • The distribution of the 'child' column in heights_mar, where some values are MAR.
In [48]:
util.multiple_kdes({'Original': heights, 'MAR, Unfilled': heights_mar})

The distributions are not very similar!

Remember that in reality, you won't get to see the turquoise distribution, which has no missing values – instead, you'll try to recreate it, using your sample with missing values.

Mean imputation of MAR data¶

Let's fill in missing values in heights_mar['child'] with the mean of the observed 'child' heights in heights_mar['child'] and see what happens.

In [49]:
heights_mar['child'].head()
Out[49]:
0    73.2
1    69.2
2     NaN
3     NaN
4    73.5
Name: child, dtype: float64
In [50]:
heights_mar_mfilled = heights_mar.fillna(heights_mar['child'].mean())
heights_mar_mfilled['child'].head()
Out[50]:
0    73.20
1    69.20
2    68.52
3    68.52
4    73.50
Name: child, dtype: float64
In [51]:
df_map = {'Original': heights, 'MAR, Unfilled': heights_mar, 'MAR, Mean Imputed': heights_mar_mfilled}
util.multiple_describe(df_map)
Out[51]:
Mean Standard Deviation
Dataset
Original 66.75 3.58
MAR, Unfilled 68.52 3.12
MAR, Mean Imputed 68.52 2.20

Note that the latter two means are biased high.

Mean imputation of MAR data¶

Let's visualize all three distributions: the original, the MAR heights with missing values, and the mean-imputed MAR heights.

In [52]:
util.multiple_kdes(df_map)

Since the sample with MAR values was already biased high, mean imputation kept the sample biased – it did not bring the data closer to the data generating process.

With our single mean imputation strategy, the resulting female mean height is biased quite high.

In [53]:
pd.concat([
    heights.groupby('gender')['child'].mean().rename('Original'),
    heights_mar.groupby('gender')['child'].mean().rename('MAR, Unfilled'),
    heights_mar_mfilled.groupby('gender')['child'].mean().rename('MAR, Mean Imputed')
], axis=1).T
Out[53]:
gender female male
Original 64.10 69.23
MAR, Unfilled 64.22 69.28
MAR, Mean Imputed 67.85 69.14

Within-group (conditional) mean imputation¶

  • Improvement: Since MAR data are MCAR within each group, we can perform group-wise mean imputation.
    • In our case, since the missingness of 'child' is dependent on 'gender', we can impute separately for each 'gender'.
    • For instance, if there is a missing 'child' height for a 'female' child, impute their height with the mean observed 'female' height.

  • With this technique, the overall mean remains unbiased, as do the within-group means.

  • Like with "single" mean imputation, the variance of the dataset is reduced.

transform returns!¶

  • In MAR data, imputation by the overall mean gives a biased estimate of the mean of each group.
  • To obtain an unbiased estimate of the mean within each group, impute using the mean within each group.
  • To perform an operation separately to each gender, we groupby('gender') and use the transform method.
In [54]:
def mean_impute(ser):
    return ser.fillna(ser.mean())

heights_mar_cond = heights_mar.groupby('gender')['child'].transform(mean_impute).to_frame()
heights_mar_cond['child'].head()
Out[54]:
0    73.20
1    69.20
2    64.22
3    64.22
4    73.50
Name: child, dtype: float64
In [55]:
df_map['MAR, Conditional Mean Imputed'] = heights_mar_cond
util.multiple_kdes(df_map)

The pink distribution does a slightly better job of approximating the turquoise distribution than the purple distribution, but not by much.

Conclusion: Imputation with single values¶

  • Imputing missing data in a column with the mean of the column:

    • faithfully reproduces the mean of the observed dataset,
    • reduces the variance, and
    • biases relationships between the column and other columns if the data are not MCAR.

  • The same is true with other statistics (e.g. median and mode).

Probabilistic imputation¶

Imputing missing values using distributions¶

  • So far, each missing value in a column has been filled in with a constant value.

    • This creates "spikes" in the imputed distributions.

  • Idea: We can probabilistically impute missing data from a distribution.

    • We can fill in missing data by drawing from the distribution of the non-missing data.
    • There are 5 missing values? Pick 5 values from the data that aren't missing.
    • How? Using np.random.choice or .sample.

Example: Probabilistic imputation in the MCAR heights dataset¶

Step 1: Determine the number of missing values in the column of interest.

In [56]:
num_null = heights_mcar['child'].isna().sum()
num_null
Out[56]:
467

Step 2: Sample that number of values from the observed values in the column of interest.

In [57]:
fill_values = np.random.choice(heights_mcar['child'].dropna(), num_null)

Step 3: Fill in the missing values with the sample from Step 2.

In [58]:
heights_mcar_pfilled = heights_mcar.copy()
heights_mcar_pfilled.loc[heights_mcar_pfilled['child'].isna(), 'child'] = fill_values

Let's look at the results.

In [59]:
df_map = {'Original': heights, 
          'MCAR, Unfilled': heights_mcar, 
          'MCAR, Probabilistically Imputed': heights_mcar_pfilled}
In [60]:
util.multiple_describe(df_map)
Out[60]:
Mean Standard Deviation
Dataset
Original 66.75 3.58
MCAR, Unfilled 66.64 3.56
MCAR, Probabilistically Imputed 66.67 3.47

Variance is preserved!

In [61]:
util.multiple_kdes(df_map)

No spikes!

Observations¶

  • With this technique, the missing values were filled in with observed values in the dataset.

  • If a value was never observed in the dataset, it will never be used to fill in a missing value.

    • For instance, if the observed heights were 68, 69, and 69.5 inches, we will never fill a missing value with 68.5 inches even though it's a perfectly reasonable height.

  • Solution? Create a histogram (with np.histogram) to bin the data, then sample from the histogram.

    • See Lab 5, Question 6.

  • Question: How would we generalize this process for MAR data?

Randomness¶

  • Unlike mean imputation, probabilistic imputation is random – each time you run the cell in which imputation is performed, the results could be different.

  • If we're interested in estimating some population parameter given our (incomplete) sample, it's best not to rely on just a single random imputation.

  • Multiple imputation: Generate multiple imputed datasets and aggregate the results!

    • Similar to bootstrapping.

Multiple imputation¶

Steps:

  1. Start with observed and incomplete data.

  2. Create $m$ imputed versions of the data through a probabilistic procedure.

    • The imputed datasets are identical for the observed data entries.
    • They differ in the imputed values.
    • The differences reflect our uncertainty about what value to impute.

  3. Then, compute parameter estimates on each imputed dataset.

    • For instance, the mean, standard deviation, median, etc.

  4. Finally, pool the $m$ parameter estimates into one estimate.

Multiple imputation¶

Let's try this procedure out on the heights_mcar dataset.

In [62]:
heights_mcar.head()
Out[62]:
father mother gender child
0 78.5 67.0 male 73.2
1 78.5 67.0 female 69.2
2 78.5 67.0 female NaN
3 78.5 67.0 female NaN
4 75.5 66.5 male 73.5
In [63]:
# This function implements the 3-step process we studied earlier.
def create_imputed(col):
    col = col.copy()
    num_null = col.isna().sum()
    fill_values = np.random.choice(col.dropna(), num_null)
    col[col.isna()] = fill_values
    return col

Each time we run the following cell, it generates a new imputed version of the 'child' column.

In [64]:
create_imputed(heights_mcar['child']).head()
Out[64]:
0    73.2
1    69.2
2    72.0
3    65.0
4    73.5
Name: child, dtype: float64

Let's run the above procedure 100 times.

In [65]:
mult_imp = pd.concat([create_imputed(heights_mcar['child']).rename(k) for k in range(100)], axis=1)
mult_imp.head()
Out[65]:
0 1 2 3 ... 96 97 98 99
0 73.2 73.2 73.2 73.2 ... 73.2 73.2 73.2 73.2
1 69.2 69.2 69.2 69.2 ... 69.2 69.2 69.2 69.2
2 73.0 62.5 72.0 72.0 ... 63.0 62.0 68.5 63.5
3 66.0 67.0 64.0 72.0 ... 72.0 62.0 69.0 67.0
4 73.5 73.5 73.5 73.5 ... 73.5 73.5 73.5 73.5

5 rows × 100 columns

Let's plot some of the imputed columns on the previous slide.

In [66]:
# Random sample of 15 imputed columns.
mult_imp_sample = mult_imp.sample(15, axis=1)
fig = ff.create_distplot(mult_imp_sample.to_numpy().T, list(mult_imp_sample.columns), show_hist=False, show_rug=False)
fig.update_xaxes(title='child')

Let's look at the distribution of means across the imputed columns.

In [67]:
px.histogram(pd.DataFrame(mult_imp.mean()), nbins=15, histnorm='probability',
             title='Distribution of Imputed Sample Means')

If the distrbution of imputed means is wide, this implies more uncertainty about what our missing values could have been – useful!

Summary, next time¶

Summary of imputation techniques¶

  • Listwise deletion.
  • Mean imputation.
  • Group-wise (conditional) mean imputation.
  • Probabilistic imputation.
  • Multiple imputation.

Summary: Listwise deletion¶

  • Procedure: df = df.dropna().
  • If data are MCAR, listwise deletion doesn't change most summary statistics (mean, median, SD) of the data.

Summary: Mean imputation¶

  • Procedure: df[col] = df[col].fillna(df[col].mean()).
  • If data are MCAR, the resulting mean is an unbiased estimate of the true mean, but the variance is too low.
  • Analogue for categorical data: imputation with the mode.

Summary: Conditional mean imputation¶

  • Procedure: for a column c1, conditional on a second categorical column

c2:

means = df.groupby('c2').mean().to_dict()
imputed = df['c1'].apply(lambda x: means[x] if np.isnan(x) else x)
  • If data are MAR, the resulting mean is an unbiased estimate of the true mean, but the variance is too low.
  • This increases correlations between the columns.
  • If the column with missing values were dependent on more than one column, we can use linear regression to predict the missing value.

Summary: Probabilistic imputation¶

  • Procedure: draw from the distribution of observed data to fill in missing values.
  • If data are MCAR, the resulting mean and variance are unbiased estimates of the true mean and variance.
  • Extending to the MAR case: draw from conditional empirical distributions.
    • If data are conditional on a single categorical column c2, apply the MCAR procedure to the groups of df.groupby(c2).

Summary: Multiple imputation¶

  • Procedure:
    • Apply probabilistic imputation multiple times, resulting in $m$ imputed datasets.
    • Compute statistics separately on the $m$ imputed datasets (e.g. compute the mean or correlation coefficient).
    • Plot the distribution of these statistics and create confidence intervals.
  • If a column is missing conditional on multiple columns, your "multiple imputations" should include probabilistic imputations for each!

Next time¶

  • Introduction to HTTP.
  • Making requests.