import pandas as pd
import numpy as np
import os

import warnings
warnings.simplefilter('ignore')

from IPython.display import display, IFrame

def show_paradox_slides():
    src = 'https://docs.google.com/presentation/d/e/2PACX-1vSbFSaxaYZ0NcgrgqZLvjhkjX-5MQzAITWAsEFZHnix3j1c0qN8Vd1rogTAQP7F7Nf5r-JWExnGey7h/embed?start=false'
    width = 960
    height = 569
    display(IFrame(src, width, height))

Lecture 5 – Pivoting and Simpson's Paradox

DSC 80, Spring 2023

Agenda

• Grouping with multiple columns.
• Pivoting.
• Distributions.
• Reshaping DataFrames.
• Simpson's paradox.
• Aside: Time series data.

Grouping

Recall, last class, we started working with a dataset that involves various measurements taken of three species of penguins in Antarctica.

import seaborn as sns
penguins = sns.load_dataset('penguins').dropna()
penguins.head()

	species	island	bill_length_mm	bill_depth_mm	flipper_length_mm	body_mass_g	sex
0	Adelie	Torgersen	39.1	18.7	181.0	3750.0	Male
1	Adelie	Torgersen	39.5	17.4	186.0	3800.0	Female
2	Adelie	Torgersen	40.3	18.0	195.0	3250.0	Female
4	Adelie	Torgersen	36.7	19.3	193.0	3450.0	Female
5	Adelie	Torgersen	39.3	20.6	190.0	3650.0	Male

penguins['species'].value_counts()

Adelie       146
Gentoo       119
Chinstrap     68
Name: species, dtype: int64

Pivoting

Mean body mass for every combination of species and island

We just found the above information by grouping by both 'species' and 'island'.

penguins.groupby(['species', 'island'])['body_mass_g'].mean()

species    island   
Adelie     Biscoe       3709.659091
           Dream        3701.363636
           Torgersen    3708.510638
Chinstrap  Dream        3733.088235
Gentoo     Biscoe       5092.436975
Name: body_mass_g, dtype: float64

But we can also create a pivot table, which contains the same information in a different orientation.

penguins.pivot_table(index='species', 
                     columns='island', 
                     values='body_mass_g', 
                     aggfunc='mean')

island	Biscoe	Dream	Torgersen
species
Adelie	3709.659091	3701.363636	3708.510638
Chinstrap	NaN	3733.088235	NaN
Gentoo	5092.436975	NaN	NaN

Let's visualize how the pivot table was created using Pandas Tutor.

%reload_ext pandas_tutor

%%pt

penguins.pivot_table(index='species', 
                     columns='island', 
                     values='body_mass_g', 
                     aggfunc='mean')

pivot_table

The pivot_table DataFrame method aggregates a DataFrame using two columns. To use it:

df.pivot_table(index=index_col,
               columns=columns_col,
               values=values_col,
               aggfunc=func)

The resulting DataFrame will have:

• One row for every unique value in index_col.
• One column for every unique value in columns_col.
• Values determined by applying func on values in values_col.

Example

Find the number of penguins per island and species.

penguins.pivot_table(index='island', 
                     columns='species', 
                     values='bill_length_mm', 
                     aggfunc='count')

species	Adelie	Chinstrap	Gentoo
island
Biscoe	44.0	NaN	119.0
Dream	55.0	68.0	NaN
Torgersen	47.0	NaN	NaN

Note that there is a NaN at the intersection of 'Biscoe' and 'Chinstrap', because there were no Chinstrap penguins on Biscoe Island.

We can either use the fillna method afterwards or the fill_value argument to fill in NaNs.

penguins.pivot_table(index='island', 
                     columns='species', 
                     values='bill_length_mm', 
                     aggfunc='count', 
                     fill_value=0)

species	Adelie	Chinstrap	Gentoo
island
Biscoe	44	0	119
Dream	55	68	0
Torgersen	47	0	0

Example

Find the median body mass per species and sex.

penguins.pivot_table(index='species', columns='sex', values='body_mass_g', aggfunc='median')

sex	Female	Male
species
Adelie	3400.0	4000.0
Chinstrap	3550.0	3950.0
Gentoo	4700.0	5500.0

Important: In penguins, each row corresponds to an individual/observation. In the pivot table above, that is no longer true.

Distributions

Joint distribution

When using aggfunc='count', a pivot table describes the joint distribution of two categorical variables. This is also called a contingency table.

counts = penguins.pivot_table(index='species', 
                              columns='sex', 
                              values='body_mass_g', 
                              aggfunc='count', 
                              fill_value=0)
counts

sex	Female	Male
species
Adelie	73	73
Chinstrap	34	34
Gentoo	58	61

We can normalize the DataFrame by dividing by the total number of penguins. The resulting numbers can be interpreted as probabilities that a randomly selected penguin from the dataset belongs to a given combination of species and sex.

joint = counts / counts.sum().sum()
joint

sex	Female	Male
species
Adelie	0.219219	0.219219
Chinstrap	0.102102	0.102102
Gentoo	0.174174	0.183183

Marginal probabilities

If we sum over one of the axes, we can compute marginal probabilities, i.e. unconditional probabilities.

joint

sex	Female	Male
species
Adelie	0.219219	0.219219
Chinstrap	0.102102	0.102102
Gentoo	0.174174	0.183183

# Recall, joint.sum(axis=0) sums across the rows, which computes the sum of the **columns**.
joint.sum(axis=0)

sex
Female    0.495495
Male      0.504505
dtype: float64

joint.sum(axis=1)

species
Adelie       0.438438
Chinstrap    0.204204
Gentoo       0.357357
dtype: float64

For instance, the second Series tells us that a randomly selected penguin has a 0.357357 chance of being of species 'Gentoo'.

Conditional probabilities

Using counts, how might we compute conditional probabilities like $$P(\text{species } = \text{"Adelie"} \mid \text{sex } = \text{"Female"})?$$

counts

sex	Female	Male
species
Adelie	73	73
Chinstrap	34	34
Gentoo	58	61

$$\begin{align*} P(\text{species} = c \mid \text{sex} = x) &= \frac{P(\text{species} = c \text{ and } \text{sex} = x)}{P(\text{sex = }x)} \\ &= \frac{\frac{\# \: (\text{species } = \: c \text{ and } \text{sex } = \: x)}{N}}{\frac{\# \: (\text{sex } = \: x)}{N}} \\ &= \frac{\# \: (\text{species} = c \text{ and } \text{sex} = x)}{\# \: (\text{sex} = x)} \end{align*}$$

Answer: To find conditional probabilities of species given sex, divide by column sums. To find conditional probabilities of sex given species, divide by row sums.

Conditional probabilities

To find conditional probabilities of species given sex, divide by column sums. To find conditional probabilities of sex given species, divide by row sums.

counts

sex	Female	Male
species
Adelie	73	73
Chinstrap	34	34
Gentoo	58	61

counts.sum(axis=0)

sex
Female    165
Male      168
dtype: int64

The conditional distribution of species given sex is below. Note that in this new DataFrame, the 'Female' and 'Male' columns each sum to 1.

counts / counts.sum(axis=0)

sex	Female	Male
species
Adelie	0.442424	0.434524
Chinstrap	0.206061	0.202381
Gentoo	0.351515	0.363095

For instance, the above DataFrame tells us that the probability that a randomly selected penguin is of species 'Adelie' given that they are of sex 'Female' is 0.442424.

Task: Try and find the conditional distribution of sex given species.

Reshaping DataFrames

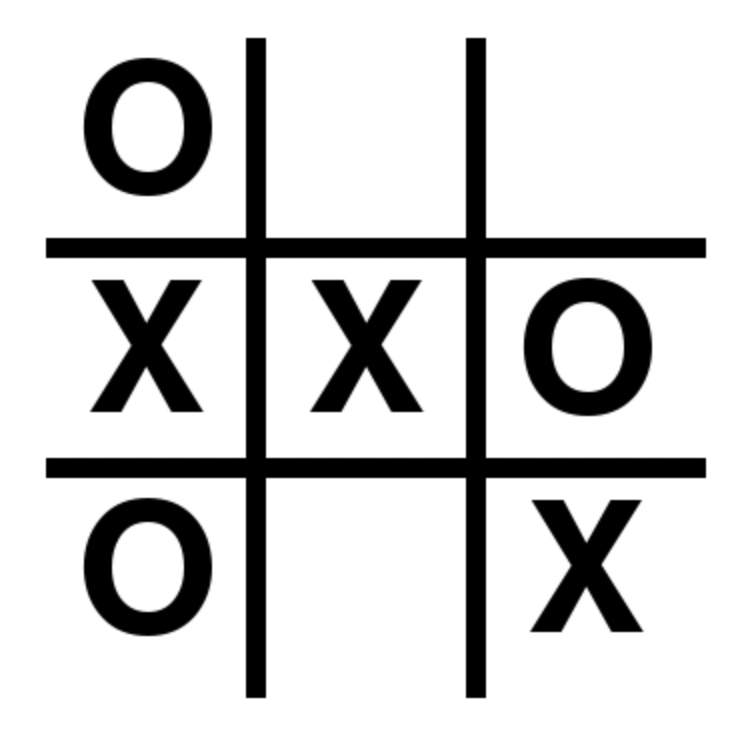
pivot_table aggregates and reshapes

• The pivot_table method does two things. It:
  • Aggregates based on two columns.
  • Reshapes the data from "long" to "wide".
    • Rows no longer correspond to observations.
• At times, we may only want to do the second step – reshape the data. To do so, we can use the pivot method.

Example: Tic-tac-toe

moves = pd.DataFrame([
    [1, 1, 'O'],
    [2, 1, 'X'],
    [2, 2, 'X'],
    [2, 3, 'O'],
    [3, 1, 'O'],
    [3, 3, 'X']
], columns=['i', 'j', 'move'])
moves

	i	j	move
0	1	1	O
1	2	1	X
2	2	2	X
3	2	3	O
4	3	1	O
5	3	3	X

moves.pivot(index='i', columns='j', values='move').fillna('')

j	1	2	3
i
1	O
2	X	X	O
3	O		X

The pivot method only reshapes a DataFrame. It does not change any of the values in it (i.e. aggfunc doesn't work with pivot).

pivot_table = groupby + pivot

• pivot_table is a shortcut for using groupby and then using pivot.
• For example, both of the following code cells find the mean body mass per species and sex.

(
    penguins.groupby(['species', 'sex'])[['body_mass_g']]
            .mean()
            .reset_index()
            .pivot(index='species', columns='sex', values='body_mass_g')
)

sex	Female	Male
species
Adelie	3368.835616	4043.493151
Chinstrap	3527.205882	3938.970588
Gentoo	4679.741379	5484.836066

penguins.pivot_table(index='species', columns='sex', values='body_mass_g', aggfunc='mean')

sex	Female	Male
species
Adelie	3368.835616	4043.493151
Chinstrap	3527.205882	3938.970588
Gentoo	4679.741379	5484.836066

aggfunc='mean' plays the same role that .mean() does.

Reshaping

• pivot_table and pivot reshape DataFrames from "long" to "wide".
• Other DataFrame reshaping methods:
  • melt: Un-pivots a DataFrame.
  • stack: Pivots multi-level columns to multi-indices.
  • unstack: Pivots multi-indices to columns.
  • Google and the documentation are your friends!

Simpson's paradox

Example: Grades

• Two students, Lisa and Bart, just finished freshman year. They both took a different number of classes in Fall, Winter, and Spring.

• Each quarter, Lisa had a higher GPA than Bart.

• But Bart has a higher overall GPA.

• How is this possible? 🤔

Run this cell to create DataFrames that contain each students' grades.

lisa = pd.DataFrame([
        [20, 46],
        [18, 54],
        [5, 20]
    ],
    columns=['Units', 'Grade Points Earned'], 
    index=['Fall', 'Winter', 'Spring'])

bart = pd.DataFrame([
        [5, 10],
        [5, 13.5],
        [22, 81.4]
    ],
    columns=['Units', 'Grade Points Earned'], 
    index=['Fall', 'Winter', 'Spring'])

Quarter-specific vs. overall GPAs

Note: The number of "grade points" earned for a course is

$$\text{number of units} \cdot \text{grade (out of 4)}$$

For instance, an A- in a 4 unit course earns $3.7 \cdot 4 = 14.8$ grade points.

lisa

	Units	Grade Points Earned
Fall	20	46
Winter	18	54
Spring	5	20

bart

	Units	Grade Points Earned
Fall	5	10.0
Winter	5	13.5
Spring	22	81.4

Lisa had a higher GPA in all three quarters:

quarterly_gpas = pd.DataFrame(
    {
        "Lisa's Quarter GPA": lisa['Grade Points Earned'] / lisa['Units'],
        "Bart's Quarter GPA": bart['Grade Points Earned'] / bart['Units']
    }
)

quarterly_gpas

	Lisa's Quarter GPA	Bart's Quarter GPA
Fall	2.3	2.0
Winter	3.0	2.7
Spring	4.0	3.7

But Lisa's overall GPA was less than Bart's overall GPA:

tot = lisa.sum()
tot['Grade Points Earned'] / tot['Units']

2.7906976744186047

tot = bart.sum()
tot['Grade Points Earned'] / tot['Units']

3.278125

What happened?

quarterly_gpas.assign(Lisa_units=lisa['Units']) \
              .assign(Bart_units=bart['Units']) \
              .iloc[:, [0, 2, 1, 3]]

	Lisa's Quarter GPA	Lisa_units	Bart's Quarter GPA	Bart_units
Fall	2.3	20	2.0	5
Winter	3.0	18	2.7	5
Spring	4.0	5	3.7	22

• When Lisa and Bart both performed poorly, Lisa took more units than Bart. This brought down 📉 Lisa's overall average.

• When Lisa and Bart both performed well, Bart took more units than Annie. This brought up 📈 Bart's overall average.

Simpson's paradox

• Simpson's paradox occurs when grouped data and ungrouped data show opposing trends.
  • It is named after Edward H. Simpson, not Lisa or Bart Simpson.

• It is purely arithmetic – it is a consequence of weighted averages.

• It often happens because there is a hidden factor (i.e. a confounder) within the data that influences results.

• Question: What is the "correct" way to summarize your data? What if you had to act on these results?

Example: How Berkeley was almost sued for gender discrimination (1973)

What do you notice?

show_paradox_slides()

What happened?

• The overall acceptance rate for women (30%) was lower than it was for men (45%).

• However, most departments (A, B, D, F) had a higher acceptance rate for women.

• Department A had a 62% acceptance rate for men and an 82% acceptance rate for women!
  • 31% of men applied to Department A.
  • 6% of women applied to Department A.

• Department F had a 6% acceptance rate for men and a 7% acceptance rate for women!
  • 14% of men applied to Department F.
  • 19% of women applied to Department F.

• Conclusion: Women tended to apply to departments with a lower acceptance rate.

Caution!

This doesn't mean that admissions are free from gender discrimination!

From Moss-Racusin et al., 2012, PNAS (cited 2600+ times):

In a randomized double-blind study (n = 127), science faculty from research-intensive universities rated the application materials of a student—who was randomly assigned either a male or female name—for a laboratory manager position. Faculty participants rated the male applicant as significantly more competent and hireable than the (identical) female applicant. These participants also selected a higher starting salary and offered more career mentoring to the male applicant. The gender of the faculty participants did not affect responses, such that female and male faculty were equally likely to exhibit bias against the female student.

But then...

From Williams and Ceci, 2015, PNAS:

Here we report five hiring experiments in which faculty evaluated hypothetical female and male applicants, using systematically varied profiles disguising identical scholarship, for assistant professorships in biology, engineering, economics, and psychology. Contrary to prevailing assumptions, men and women faculty members from all four fields preferred female applicants 2:1 over identically qualified males with matching lifestyles (single, married, divorced), with the exception of male economists, who showed no gender preference.

Do these conflict?

Not necessarily. One explanation, from William and Ceci:

Instead, past studies have used ratings of students’ hirability for a range of posts that do not include tenure-track jobs, such as managing laboratories or performing math assignments for a company. However, hiring tenure-track faculty differs from hiring lower-level staff: it entails selecting among highly accomplished candidates, all of whom have completed Ph.D.s and amassed publications and strong letters of support. Hiring bias may occur when applicants’ records are ambiguous, as was true in studies of hiring bias for lower-level staff posts, but such bias may not occur when records are clearly strong, as is the case with tenure-track hiring.

Do these conflict?

From Witteman, et al, 2019, in The Lancet:

Thus, evidence of scientists favouring women comes exclusively from hypothetical scenarios, whereas evidence of scientists favouring men comes from hypothetical scenarios and real behaviour. This might reflect academics' growing awareness of the social desirability of achieving gender balance, while real academic behaviour might not yet put such ideals into action.

Example: Restaurant reviews and phone types

• You are deciding whether to eat at Dirty Birds or The Loft.

• Suppose Yelp shows ratings aggregated by phone type (Android vs. iPhone).

Phone Type	Stars for Dirty Birds	Stars for The Loft
Android	4.24	4.0
iPhone	2.99	2.79
All	3.32	3.37

• Question: Should you choose Dirty Birds or The Loft?

• Answer: The type of phone you use likely has nothing to do with your taste in food – pick the restaurant that is rated higher overall.

• Remember, Simpson's paradox is merely a property of weighted averages!

Verifying Simpson's paradox

ratings_path = os.path.join('data', 'ratings.csv')
ratings = pd.read_csv(ratings_path)
ratings.sample(5).head()

	phone	restaurant	rating
4441	iPhone	The Loft	3
2184	iPhone	Dirty Birds	2
1085	Android	The Loft	4
616	Android	Dirty Birds	5
102	Android	Dirty Birds	4

ratings['phone'].value_counts(normalize=True)

iPhone     0.651452
Android    0.348548
Name: phone, dtype: float64

Aggregated means:

ratings.pivot_table(index='phone', columns='restaurant', values='rating', aggfunc='mean')

restaurant	Dirty Birds	The Loft
phone
Android	4.235669	4.000000
iPhone	2.987957	2.787971

ratings.pivot_table(index='phone', columns='restaurant', values='rating', aggfunc='count')

restaurant	Dirty Birds	The Loft
phone
Android	785	895
iPhone	2159	981

Disaggregated means:

ratings.groupby('restaurant').mean()

	rating
restaurant
Dirty Birds	3.320652
The Loft	3.366205

Takeaways

Be skeptical of...

• Aggregate statistics.
• People misusing statistics to "prove" that discrimination doesn't exist.
• Drawing conclusions from individual publications ($p$-hacking, publication bias, narrow focus, etc.).
• Everything!

Further reading

• Gender Bias in Admission Statistics?
  • Contains a great visualization.
• Simpson's paradox on Wikipedia.

Aside: Working with time series data

Time series – why now?

• Next lecture, we'll start looking at how to combine multiple DataFrames.
• Data is often partitioned by time. For instance, there may be one .csv file per day for 1 year.
• We will need to load in the files as DataFrames and pd.concat them together.
• Note: "time series" is a general term and is not related to Series in pandas.

Datetime types

When working with time data, you will see two different kinds of "times":

• Datetimes reference particular moments in time (e.g. November 26th, 1998 at 8:26AM).
  • Could just be a date, e.g. January 20, 2023.
  • Could just be a time, e.g. 4:45 AM.
  • Datetimes typically don't keep track of timezones.

• Timedeltas, or durations, reference an exact length of time (e.g. a duration of 3 hours).

The datetime module

Python has an in-built datetime module, which contains datetime and timedelta types. These are much more convenient to deal with than strings that contain times.

import datetime

datetime.datetime.now()

datetime.datetime(2023, 4, 12, 10, 47, 41, 78224)

datetime.datetime.now() + datetime.timedelta(days=3, hours=5)

datetime.datetime(2023, 4, 15, 15, 47, 41, 82060)

Unix timestamps count the number of seconds since January 1st, 1970.

datetime.datetime.now().timestamp()

1681321661.085464

Times in pandas

• pd.Timestamp is the pandas equivalent of datetime.
• pd.to_datetime converts strings to pd.Timestamp objects.

pd.Timestamp(year=1998, month=11, day=26)

Timestamp('1998-11-26 00:00:00')

final_start = pd.to_datetime('March 22nd, 2023, 11:30AM')
final_start

Timestamp('2023-03-22 11:30:00')

final_finish = pd.to_datetime('March 22nd, 2023, 2:30PM')
final_finish

Timestamp('2023-03-22 14:30:00')

Timestamps have time-related attributes, e.g. dayofweek, hour, min, sec.

# 0 is Monday, 1 is Tuesday, etc.
final_finish.dayofweek

2

final_finish.year

2023

Subtracting timestamps yields pd.Timedelta objects.

final_finish - final_start

Timedelta('0 days 03:00:00')

Example: Exam speeds

Below, we have the Final Exam starting and ending times for two sections of a course.

exam_times_path = os.path.join('data', 'exam-times.csv')
exam_times = pd.read_csv(exam_times_path)
exam_times

	name	start_exam	finish_exam	section
0	Annie	15:00	16:00	A
1	Billy	15:02	17:58	A
2	Sally	15:01	17:05	A
3	Tommy	15:00	16:55	A
4	Junior	18:00	20:00	B
5	Rex	18:06	20:50	B
6	Flash	19:07	20:59	B

Question: Who took the longest time to finish the exam?

# Step 1: Convert the time columns to timestamps, using pd.to_datetime.
exam_times['start_exam'] = pd.to_datetime(exam_times['start_exam'])
exam_times['finish_exam'] = pd.to_datetime(exam_times['finish_exam'])
exam_times

	name	start_exam	finish_exam	section
0	Annie	2023-04-12 15:00:00	2023-04-12 16:00:00	A
1	Billy	2023-04-12 15:02:00	2023-04-12 17:58:00	A
2	Sally	2023-04-12 15:01:00	2023-04-12 17:05:00	A
3	Tommy	2023-04-12 15:00:00	2023-04-12 16:55:00	A
4	Junior	2023-04-12 18:00:00	2023-04-12 20:00:00	B
5	Rex	2023-04-12 18:06:00	2023-04-12 20:50:00	B
6	Flash	2023-04-12 19:07:00	2023-04-12 20:59:00	B

# Note that datetime64[ns] is the data type pandas uses to store timestamps in a Series/DataFrame.
exam_times.dtypes

name                   object
start_exam     datetime64[ns]
finish_exam    datetime64[ns]
section                object
dtype: object

# Step 2: Find the difference between the two time columns.
exam_times['difference'] = exam_times['finish_exam'] - exam_times['start_exam']
exam_times

	name	start_exam	finish_exam	section	difference
0	Annie	2023-04-12 15:00:00	2023-04-12 16:00:00	A	0 days 01:00:00
1	Billy	2023-04-12 15:02:00	2023-04-12 17:58:00	A	0 days 02:56:00
2	Sally	2023-04-12 15:01:00	2023-04-12 17:05:00	A	0 days 02:04:00
3	Tommy	2023-04-12 15:00:00	2023-04-12 16:55:00	A	0 days 01:55:00
4	Junior	2023-04-12 18:00:00	2023-04-12 20:00:00	B	0 days 02:00:00
5	Rex	2023-04-12 18:06:00	2023-04-12 20:50:00	B	0 days 02:44:00
6	Flash	2023-04-12 19:07:00	2023-04-12 20:59:00	B	0 days 01:52:00

exam_times.dtypes

name                    object
start_exam      datetime64[ns]
finish_exam     datetime64[ns]
section                 object
difference     timedelta64[ns]
dtype: object

# Step 3: Sort by the difference in descending order and take the first row.
exam_times.sort_values('difference', ascending=False)['name'].iloc[0]

'Billy'

Summary, next time

Summary

• pivot_table aggregates data based on two categorical columns, and reshapes the result to be "wide" instead of "long".
• Simpson's paradox occurs when grouped data and ungrouped data show opposing trends.
  • It is a consequence of arithmetic.
• Timestamps in pandas are stored using pd.Timestamp and pd.Timedelta objects.

Next time

Combining DataFrames.