In [1]:
import pandas as pd
import numpy as np
import os

import plotly.express as px
import plotly.graph_objects as go
pd.options.plotting.backend = 'plotly'
TEMPLATE = 'seaborn'

# Carryover setup from last lecture
import seaborn as sns
tips = sns.load_dataset('tips')

from sklearn.linear_model import LinearRegression

import util

import warnings
warnings.simplefilter('ignore')

Lecture 23 – Cross-Validation¶

DSC 80, Spring 2023¶

Agenda¶

  • Generalization.
  • Train-test split.
  • Hyperparameters.
  • Cross-validation.

Generalization¶

Recall, last time, we drew two samples from the same data generating process, and fit polynomials of degree 1, 3, and 25 on each sample.

In [2]:
np.random.seed(23) # For reproducibility.

def sample_dgp(n=100):
    x = np.linspace(-2, 3, n)
    y = x ** 3 + (np.random.normal(0, 3, size=n))
    return pd.DataFrame({'x': x, 'y': y})

sample_1 = sample_dgp()
sample_2 = sample_dgp()

When trained on sample 1, the degree 25 polynomial had the lowest RMSE on sample 1.

In [3]:
# Look at the definition of train_and_plot in util.py if you're curious as to how the plotting works.
fig = util.train_and_plot(train_sample=sample_1, test_sample=sample_1, degs=[1, 3, 25])
fig.update_layout(title='Trained on Sample 1, Performance on Sample 1')

But, when trained on sample 1, the degree 3 polynomial had the lowest RMSE on sample 2.

In [4]:
fig = util.train_and_plot(train_sample=sample_1, test_sample=sample_2, degs=[1, 3, 25])
fig.update_layout(title='Trained on Sample 1, Performance on Sample 2')

If we train polynomials of degree 1, 3, and 25 on each sample, we see that the degree 25 polynomials vary more than the degree 1 and 3 polynomials do.

In [5]:
util.plot_multiple_models(sample_1, sample_2, degs=[1, 3, 25])

Bias and variance¶

The training data we have access to is a sample from the DGP. We are concerned with our model's ability to generalize and work well on different datasets drawn from the same DGP.

Suppose we fit a model $H$ (e.g. a degree 3 polynomial) on several different datasets from a DGP. There are three sources of error that arise:

  • ⭐️ Bias: The expected deviation between a predicted value and an actual value.
    • In other words, for a given $x_i$, how far is $H(x_i)$ from the true $y_i$, on average?
    • Low bias is good! ✅
    • High bias is a sign of underfitting, i.e. that our model is too basic to capture the relationship between our features and response.
  • ⭐️ Model variance ("variance"): The variance of a model's predictions.
    • In other words, for a given $x_i$, what is the variance of $H(x_i)$ across all datasets?
    • Low model variance is good! ✅
    • High model variance is a sign of overfitting, i.e. that our model is too complicated and is prone to fitting to the noise in our training data.
  • Observation variance: The variance due to the random noise in the process we are trying to model (e.g. measurement error). We can't control this, without collecting more data!

Here, suppose:

  • The red bulls-eye represents your true weight and height 🧍.
  • The dark blue darts represent predictions of your weight and height using different models that were fit on the same DGP.

We'd like our models to be in the top left, but in practice that's hard to achieve!

Train-test split¶

Avoiding overfitting¶

  • We won't know whether our model has overfit to our sample (training data) unless we get to see how well it performs on a new sample from the same DGP.
  • 💡Idea: Split our sample into a training set and test set.
  • Use only the training set to fit the model (i.e. find $w^*$).
  • Use the test set to evaluate the model's error (RMSE, $R^2$).
  • The test set is like a new sample of data from the same DGP as the training data!
    • Similar to bootstrapping (but not quite the same, because there is no resampling involved).
    • If our sample is not representative of the DGP, this method has limited effectiveness!

Train-test split 🚆¶

sklearn.model_selection.train_test_split implements a train-test split for us! 🙏🏼

If X is an array/DataFrame of features and y is an array/Series of responses,

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)

randomly splits the features and responses into training and test sets, such that the test set contains 0.25 of the full dataset.

In [6]:
from sklearn.model_selection import train_test_split
In [7]:
# Read the documentation!
train_test_split?

Let's perform a train/test split on our tips dataset.

In [8]:
X = tips.drop('tip', axis=1)
y = tips['tip']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) # We don't have to choose 0.25.

Before proceeding, let's check the sizes of X_train and X_test.

In [9]:
print('Rows in X_train:', X_train.shape[0])
display(X_train.head())
print('Rows in X_test:', X_test.shape[0])
display(X_test.head())

Rows in X_train: 195
total_bill sex smoker day time size
4 24.59 Female No Sun Dinner 4
209 12.76 Female Yes Sat Dinner 2
178 9.60 Female Yes Sun Dinner 2
230 24.01 Male Yes Sat Dinner 4
5 25.29 Male No Sun Dinner 4 
Rows in X_test: 49
total_bill sex smoker day time size
146 18.64 Female No Thur Lunch 3
224 13.42 Male Yes Fri Lunch 2
134 18.26 Female No Thur Lunch 2
131 20.27 Female No Thur Lunch 2
147 11.87 Female No Thur Lunch 2
In [10]:
X_train.shape[0] / tips.shape[0]
Out[10]:
0.7991803278688525

Example train-test split¶

Steps:

  1. Fit a model on the training set.
  2. Evaluate the model on the test set.
In [11]:
tips.head()
Out[11]:
total_bill tip sex smoker day time size
0 16.99 1.01 Female No Sun Dinner 2
1 10.34 1.66 Male No Sun Dinner 3
2 21.01 3.50 Male No Sun Dinner 3
3 23.68 3.31 Male No Sun Dinner 2
4 24.59 3.61 Female No Sun Dinner 4
In [12]:
X = tips[['total_bill', 'size']] # For this example, we'll use just the already-quantitative columns in tips.
y = tips['tip']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1) # random_state is like np.random.seed.

Here, we'll use a stand-alone LinearRegression model without a Pipeline, but this process would work the same if we were using a Pipeline.

In [13]:
lr = LinearRegression()
lr.fit(X_train, y_train)
Out[13]:
LinearRegression()

Let's check our model's performance on the training set first.

In [14]:
from sklearn.metrics import mean_squared_error # Built-in RMSE/MSE function.
In [15]:
pred_train = lr.predict(X_train)
rmse_train = mean_squared_error(y_train, pred_train, squared=False)
rmse_train
Out[15]:
0.9803205287924737

And the test set:

In [16]:
pred_test = lr.predict(X_test)
rmse_test = mean_squared_error(y_test, pred_test, squared=False)
rmse_test
Out[16]:
1.138177129113125

Since rmse_train and rmse_test are similar, it doesn't seem like our model is overfitting to the training data. If rmse_test was much larger than rmse_train, it would be evidence that our model is unable to generalize well.

Hyperparameters¶

Example: Polynomial regression¶

We recently looked at an example of polynomial regression.

In [17]:
fig = util.train_and_plot(train_sample=sample_1, test_sample=sample_2, degs=[1, 3, 25])
fig.update_layout(title='Trained on Sample 1, Performance on Sample 2')

When building these models:

  • We got to choose the degree of the polynomials (i.e. we chose 1, 3, and 25).
  • We didn't get to choose the exact formulas for the three polynomials – their formulas were learned from data.

Parameters vs. hyperparameters¶

  • A parameter defines the relationship between variables in a model.

    • We learn parameters from data.
    • For instance, suppose we fit a degree 3 polynomial to data, and end up with

    $$H(x) = 1 - 2x + 13x^2 - 4x^3$$

    • 1, -2, 13, and -4 are parameters.
  • A hyperparameter is a parameter that we get to choose before our model is fit to the data.
    • Think of hyperparameters as knobs 🎛 – we get to pick and tune them!
    • Polynomial degree was a hyperparameter in the previous example, and we tried three different values – 1, 3, and 25.
  • Question: How do we choose the "right" hyperparameter(s)?

Training error vs. test error¶

  • We know that a model's performance on a test set is a good estimate of its ability to generalize to unseen data.
  • We want to find the hyperparameter that leads to the best test set performance.
  • Idea:
    1. Come up with a list of hyperparameters to try.
    2. For each hyperparameter, train the model on the training set and compute its performance on the test set.
    3. Pick the hyperparameter with the best performance on the test set.

Training error vs. test error¶

  • Let's try this strategy on sample 1 from our earlier example.
  • We'll try to fit a polynomial model on the dataset; we'll choose the polynomial's degree from the list [1, 2, ..., 25].
In [18]:
px.scatter(sample_1, x='x', y='y', title='Sample 1', template=TEMPLATE)

First, we perform a train-test split.

In [19]:
X = sample_1[['x']]
y = sample_1['y']

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=100)

Then, we'll implement the logic from the previous slide.

In [20]:
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
In [21]:
train_errs = []
test_errs = []

for d in range(1, 26):
    pl = Pipeline([('poly', PolynomialFeatures(d)), ('lin-reg', LinearRegression())])
    pl.fit(X_train, y_train)
    train_errs.append(mean_squared_error(y_train, pl.predict(X_train), squared=False))
    test_errs.append(mean_squared_error(y_test, pl.predict(X_test), squared=False))

Let's look at the plots of training error vs. degree and test error vs. degree.

In [22]:
fig = go.Figure()

fig.add_trace(
    go.Scatter(x=np.arange(1, 26), y=train_errs, name='Training Error')
)

fig.add_trace(
    go.Scatter(x=np.arange(1, 26), y=test_errs, name='Test Error', line={'color': 'orange'})
)

fig.update_layout(showlegend=True, xaxis_title='Degree', yaxis_title='RMSE')
  • Training error appears to decrease as polynomial degree increases.
  • Test error appears to decrease until a "valley", and then increases again.
  • Here, we'd choose a degree of 3, since that degree has the lowest test error.

Training error vs. test error¶

The pattern we saw in the previous example is true more generally.

We pick the hyperparameter(s) at the "valley" of test error.

Note that training error tends to underestimate test error, but it doesn't have to – i.e., it is possible for test error to be lower than training error (say, if the test set is "easier" to predict than the training set).

Conducting train-test splits¶

  • Recall, training data is used to fit our model, and test data is used to evaluate our model.
  • Question: How should we split?
    • sklearn's train_test_split splits randomly, which usually works well.
    • However, if there is some element of time in the training data (say, when predicting the future price of a stock), a better split is "past" and "future".
  • Question: How large should the split be, e.g. 90%-10% vs. 75%-25%?
    • There's a tradeoff – a larger training set should lead to a "better" model, while a larger test set should lead to a better estimate of our model's ability to generalize.
    • There's no "right" choice, but we usually choose between a split between the ranges above.

But wait...¶

  • With our current strategy, we are choosing the hyperparameter that creates the model that performs best on the test set.
  • As such, we are overfitting to the test set – the best hyperparameter for the test set might not be the best hyperparameter for a totally unseen dataset!
  • It seems like we need another split.

Cross-validation¶

A single validation set¶

  1. Split the data into three sets: training, validation, and test.
  1. For each hyperparameter choice, train the model only on the training set, and evaluate the model's performance on the validation set.
  1. Find the hyperparameter with the best validation performance.
  1. Retrain the final model on the training and validation sets, and report its performance on the test set.

Issue: This strategy is too dependent on the validation set, which may be small and/or not a representative sample of the data.

$k$-fold cross-validation¶

Instead of relying on a single validation set, we can create $k$ validation sets, where $k$ is some positive integer (5 in the example below).

Since each data point is used for training $k-1$ times and validation once, the (averaged) validation performance should be a good metric of a model's ability to generalize to unseen data.

$k$-fold cross-validation (or simply "cross-validation") is the technique we will use for finding hyperparameters.

Creating folds in sklearn¶

sklearn has a KFold class that splits data into training and validation folds.

In [23]:
from sklearn.model_selection import KFold

Let's use a simple dataset for illustration.

In [24]:
data = np.arange(10, 70, 10)
data
Out[24]:
array([10, 20, 30, 40, 50, 60])

Let's instantiate a KFold object with $k=3$.

In [25]:
kfold = KFold(3, shuffle=True, random_state=1)
kfold
Out[25]:
KFold(n_splits=3, random_state=1, shuffle=True)

Finally, let's use kfold to split data:

In [26]:
for train, val in kfold.split(data):
    print(f'train: {data[train]}, validation: {data[val]}')

train: [10 40 50 60], validation: [20 30]
train: [20 30 40 60], validation: [10 50]
train: [10 20 30 50], validation: [40 60]

Note that each value in data is used for validation exactly once and for training exactly twice. Also note that because we set shuffle=True the groups are not simply [10, 20], [30, 40], and [50, 60].

$k$-fold cross-validation¶

First, shuffle the dataset randomly and split it into $k$ disjoint groups. Then:

  • For each hyperparameter:
    • For each unique group:
      • Let the unique group be the "validation set".
      • Let all other groups be the "training set".
      • Train a model using the selected hyperparameter on the training set.
      • Evaluate the model on the validation set.
    • Compute the average validation score (e.g. RMSE) for the particular hyperparameter.
  • Choose the hyperparameter with the best average validation score.

$k$-fold cross-validation in sklearn¶

While you could manually use KFold to perform cross-validation, the cross_val_score function in sklearn implements $k$-fold cross-validation for us!

cross_val_score(estimator, X_train, y_train, cv)

Specifically, it takes in:

  • A Pipeline or estimator that has not already been fit.
  • Training data.
  • A value of $k$ (through the cv argument).
  • (Optionally) A scoring metric.

and performs $k$-fold cross-validation, returning the values of the scoring metric on each fold.

In [27]:
from sklearn.model_selection import cross_val_score

$k$-fold cross-validation in sklearn¶

  • Let's perform $k$-fold cross validation in order to help us pick a degree for polynomial regression from the list [1, 2, ..., 25].
  • We'll use $k=5$ since it's a common choice (and the default in sklearn).
  • For the sake of this example, we'll suppose sample_1 is our "training + validation data", i.e. that our test data is in some other dataset.
    • If this were not true, we'd first need to split sample_1 into separate training and test sets.
In [28]:
errs_df = pd.DataFrame()

for d in range(1, 26):
    pl = Pipeline([('poly', PolynomialFeatures(d)), ('lin-reg', LinearRegression())])
    
    # The `scoring` argument is used to specify that we want to compute the RMSE; 
    # the default is R^2. It's called "neg" RMSE because, 
    # by default, sklearn likes to "maximize" scores, and maximizing -RMSE is the same
    # as minimizing RMSE.
    errs = cross_val_score(pl, sample_1[['x']], sample_1['y'], 
                           cv=5, scoring='neg_root_mean_squared_error')
    errs_df[f'Deg {d}'] = -errs # Negate to turn positive (sklearn computed negative RMSE).
    
errs_df.index = [f'Fold {i}' for i in range(1, 6)]
errs_df.index.name = 'Validation Fold'

Next class, we'll look at how to implement this procedure without needing to for-loop over values of d.

$k$-fold cross-validation in sklearn¶

Note that for each choice of degree (our hyperparameter), we have five RMSEs, one for each "fold" of the data. This means that in total, 125 models were trained/fit to data!

In [29]:
errs_df
Out[29]:
Deg 1 Deg 2 Deg 3 Deg 4 Deg 5 Deg 6 Deg 7 Deg 8 Deg 9 Deg 10 ... Deg 16 Deg 17 Deg 18 Deg 19 Deg 20 Deg 21 Deg 22 Deg 23 Deg 24 Deg 25
Validation Fold
Fold 1 4.789975 12.814865 5.040947 4.927487 8.853939 13.150006 18.023855 149.574851 897.759319 718.403458 ... 175100.068052 1.104271e+06 2.266879e+06 1.240114e+06 4.321905e+06 7.223294e+07 8.776463e+06 6.569429e+07 1.412632e+08 5.904442e+08
Fold 2 3.971600 5.359234 3.186076 3.218728 3.194274 3.007987 3.077643 3.127204 3.098704 3.559998 ... 4.123032 5.588813e+00 5.634207e+00 9.640386e+00 2.285274e+01 2.299261e+01 2.929238e+01 7.850249e+01 7.527421e+01 3.134011e+01
Fold 3 4.770176 2.557932 2.083676 2.110708 2.100757 2.013973 2.018524 1.996626 2.186183 3.946495 ... 2.682152 2.764271e+00 2.563292e+00 2.743327e+00 1.790691e+01 1.786843e+01 3.029923e+01 3.090558e+01 4.242389e+01 3.723872e+01
Fold 4 6.134098 4.656187 2.925225 2.932392 3.030811 3.040322 3.144730 3.160528 3.310559 3.070833 ... 7.248788 3.234748e+00 3.065008e+00 1.165178e+01 7.484082e+00 7.543781e+00 6.274907e+00 3.328220e+01 5.804341e+01 9.691200e+00
Fold 5 11.699003 11.916631 3.235882 4.372698 33.584482 51.745272 56.510688 92.223491 335.804723 1168.510898 ... 90577.446204 8.722900e+05 9.204615e+05 8.464799e+06 2.191781e+07 6.018466e+07 8.361500e+06 2.276297e+08 8.168459e+08 6.625413e+09

5 rows × 25 columns

We should choose the degree with the lowest average validation RMSE.

In [30]:
errs_df.mean().idxmin()
Out[30]:
'Deg 3'

Note that if we didn't perform $k$-fold cross-validation, but instead just used a single validation set, we may have ended up with a different result:

In [31]:
errs_df.idxmin(axis=1)
Out[31]:
Validation Fold
Fold 1    Deg 1
Fold 2    Deg 6
Fold 3    Deg 8
Fold 4    Deg 3
Fold 5    Deg 3
dtype: object

*Note*: You may notice that the RMSEs in Folds 1 and 5 are significantly higher than in other folds. Can you think of reasons why, and how we might fix this?

In [32]:
px.scatter(sample_1, x='x', y='y', title='Sample 1', template=TEMPLATE)

Another example: Tips¶

We can also use $k$-fold cross-validation to determine which subset of features to use in a linear model that predicts tips (though, as you'll see, the code is not pretty).

In [33]:
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import FunctionTransformer, OneHotEncoder

As we should always do, we'll perform a train-test split on tips and will only use the training data for cross-validation.

In [34]:
X = tips.drop('tip', axis=1)
y = tips['tip']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
In [35]:
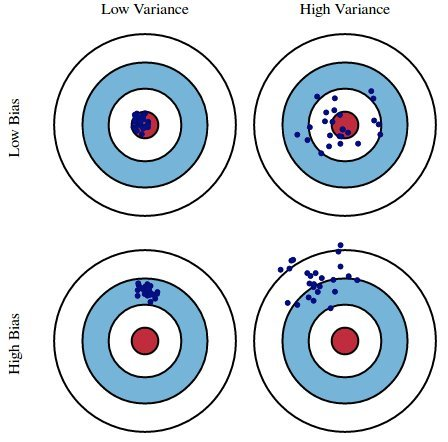
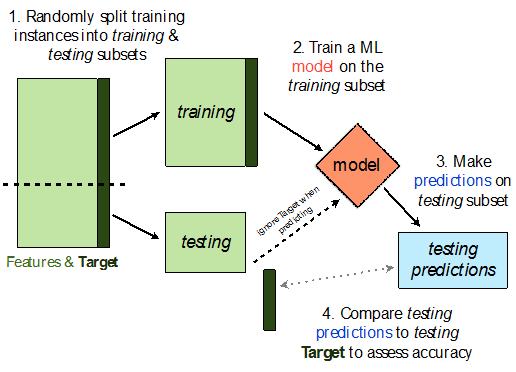
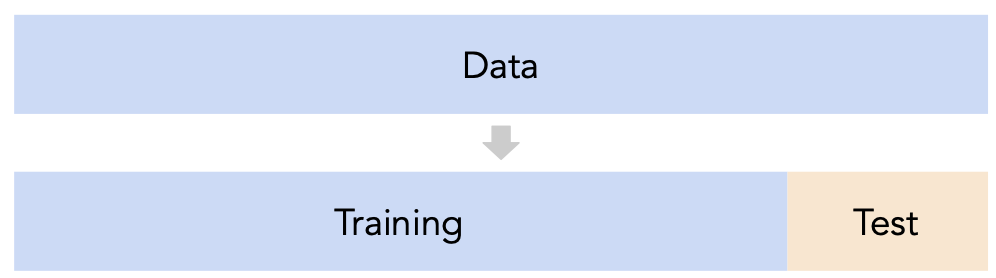
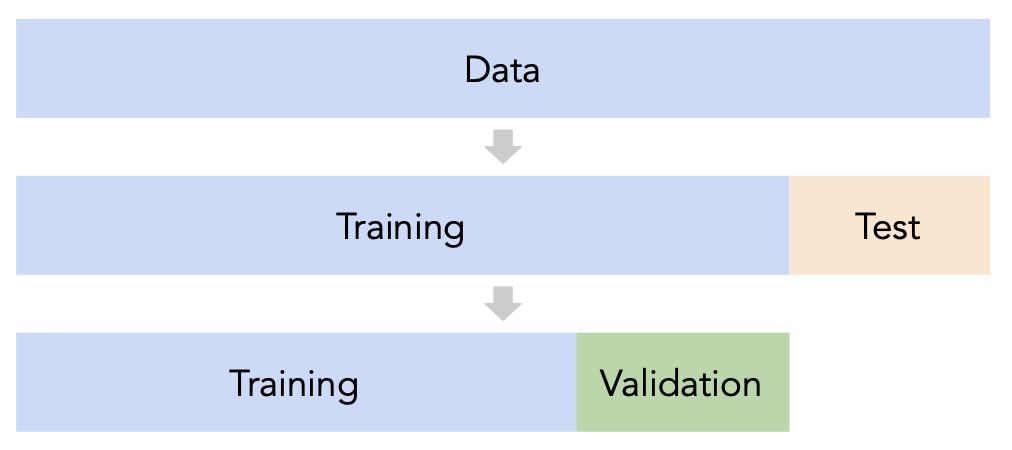
# A dictionary that maps names to Pipeline objects.
pipes = {
    'total_bill only': Pipeline([
        ('trans', ColumnTransformer(
            [('keep', FunctionTransformer(lambda x: x), ['total_bill'])], 
            remainder='drop')), 
        ('lin-reg', LinearRegression())
    ]),
    'total_bill + size': Pipeline([
        ('trans', ColumnTransformer(
            [('keep', FunctionTransformer(lambda x: x), ['total_bill', 'size'])], 
            remainder='drop')), 
        ('lin-reg', LinearRegression())
    ]),
    'total_bill + size + OHE smoker': Pipeline([
        ('trans', ColumnTransformer(
            [('keep', FunctionTransformer(lambda x: x), ['total_bill', 'size']),
             ('ohe', OneHotEncoder(), ['smoker'])], 
            remainder='drop')), 
        ('lin-reg', LinearRegression())
    ]),
    'total_bill + size + OHE all': Pipeline([
        ('trans', ColumnTransformer(
            [('keep', FunctionTransformer(lambda x: x), ['total_bill', 'size']),
             ('ohe', OneHotEncoder(), ['smoker', 'sex', 'time', 'day'])], 
            remainder='drop')), 
        ('lin-reg', LinearRegression())
    ]),
}
In [36]:
pipe_df = pd.DataFrame()

for pipe in pipes:
    errs = cross_val_score(pipes[pipe], X_train, y_train,
                           cv=5, scoring='neg_root_mean_squared_error')
    pipe_df[pipe] = -errs
    
pipe_df.index = [f'Fold {i}' for i in range(1, 6)]
pipe_df.index.name = 'Validation Fold'
In [37]:
pipe_df
Out[37]:
total_bill only total_bill + size total_bill + size + OHE smoker total_bill + size + OHE all
Validation Fold
Fold 1 1.321421 1.273630 1.269500 1.294183
Fold 2 0.951671 0.921717 0.929099 0.934066
Fold 3 0.774420 0.864801 0.858623 0.867915
Fold 4 0.848454 0.838873 0.835130 0.860885
Fold 5 1.102937 1.070329 1.069948 1.083139
In [38]:
pipe_df.mean()
Out[38]:
total_bill only                   0.999780
total_bill + size                 0.993870
total_bill + size + OHE smoker    0.992460
total_bill + size + OHE all       1.008038
dtype: float64
In [39]:
pipe_df.mean().idxmin()
Out[39]:
'total_bill + size + OHE smoker'

Even though the third model has the lowest average validation RMSE, its average validation RMSE is very close to that of the other, simpler models, and as a result we'd likely use the simplest model in practice.

Summary: Generalization¶

  1. Split the data into two sets: training and test.

  2. Use only the training data when designing, training, and tuning the model.

    • Use $k$-fold cross-validation to choose hyperparameters and estimate the model's ability to generalize.
    • Do not ❌ look at the test data in this step!

  3. Commit to your final model and train it using the entire training set.

  4. Test the data using the test data. If the performance (e.g. RMSE) is not acceptable, return to step 2.

  5. Finally, train on all available data and ship the model to production! 🛳

🚨 This is the process you should always use! 🚨

Discussion Question 🤔¶

  • Suppose you have a training dataset with 1000 rows.
  • You want to decide between 20 hyperparameters for a particular model.
  • To do so, you perform 10-fold cross-validation.
  • How many times is the first row in the training dataset (X.iloc[0]) used for training a model?

Summary, next time¶

Summary¶

  • A model's training error tends to decrease as model complexity increases, while its test error tends to decrease, before reaching a "sweet spot" and increasing again.
  • A hyperparameter is a configuration that we choose before training a model; an important task in machine learning is selecting "good" hyperparameters.
  • In order to quantify a model's ability to generalize to unseen data, use $k$-fold cross-validation.
    • In particular, $k$-fold CV is used to select hyperparameters.

Next time¶

  • Example: Decision trees 🌲.
  • Tuning multiple hyperparameters at once.
  • Multicollinearity (time permitting).