In [1]:
import pandas as pd
import numpy as np
import os

import matplotlib.pyplot as plt
import plotly.express as px
import plotly.graph_objects as go
pd.options.plotting.backend = 'plotly'
TEMPLATE = 'seaborn'

import warnings
warnings.simplefilter('ignore')

Lecture 26 – Classifier Evaluation¶

DSC 80, Spring 2023¶

Agenda¶

  • Classifier evaluation.
    • Example: Tumor malignancy prediction (via logistic regression).

Classifier evaluation¶

Accuracy isn't everything!¶

$$\text{accuracy} = \frac{\text{# data points classified correctly}}{\text{# data points}}$$
  • Accuracy is defined as the proportion of predictions that are correct.
  • It weighs all correct predictions the same, and weighs all incorrect predictions the same.
  • But some incorrect predictions may be worse than others!
    • Example: Suppose you take a COVID test 🦠. Which is worse:
      • The test saying you have COVID, when you really don't, or
      • The test saying you don't have COVID, when you really do?

The Boy Who Cried Wolf 👦😭🐺¶

(source)

A shepherd boy gets bored tending the town's flock. To have some fun, he cries out, "Wolf!" even though no wolf is in sight. The villagers run to protect the flock, but then get really mad when they realize the boy was playing a joke on them.

Repeat the previous paragraph many, many times.

One night, the shepherd boy sees a real wolf approaching the flock and calls out, "Wolf!" The villagers refuse to be fooled again and stay in their houses. The hungry wolf turns the flock into lamb chops. The town goes hungry. Panic ensues.

The wolf classifier¶

  • Predictor: Shepherd boy.
  • Positive prediction: "There is a wolf."
  • Negative prediction: "There is no wolf."

Some questions to think about:

  • What is an example of an incorrect, positive prediction?
  • Was there a correct, negative prediction?
  • There are four possibilities. What are the consequences of each?
    • (predict yes, predict no) x (actually yes, actually no).

The wolf classifier¶

Below, we present a confusion matrix, which summarizes the four possible outcomes of the wolf classifier.

Screen%20Shot%202019-03-03%20at%206.05.29%20PM.png

Outcomes in binary classification¶

When performing binary classification, there are four possible outcomes.

(Note: A "positive prediction" is a prediction of 1, and a "negative prediction" is a prediction of 0.)

Outcome of Prediction Definition True Class
True positive (TP) ✅ The predictor correctly predicts the positive class. P
False negative (FN) ❌ The predictor incorrectly predicts the negative class. P
True negative (TN) ✅ The predictor correctly predicts the negative class. N
False positive (FP) ❌ The predictor incorrectly predicts the positive class. N
⬇️
Predicted Negative Predicted Positive
Actually Negative TN ✅ FP ❌
Actually Positive FN ❌ TP ✅

The confusion matrix above is organized the same way that sklearn's confusion matrices are (but differently than in the wolf example).

Note that in the four acronyms – TP, FN, TN, FP – the first letter is whether the prediction is correct, and the second letter is what the prediction is.

Example: COVID testing 🦠¶

  • UCSD Health administers hundreds of COVID tests a day. The tests are not fully accurate.
  • Each test comes back either
    • positive, indicating that the individual has COVID, or
    • negative, indicating that the individual does not have COVID.
  • Question: What is a TP in this scenario? FP? TN? FN?
  • TP: The test predicted that the individual has COVID, and they do ✅.
  • FP: The test predicted that the individual has COVID, but they don't ❌.
  • TN: The test predicted that the individual doesn't have COVID, and they don't ✅.
  • FN: The test predicted that the individual doesn't have COVID, but they do ❌.

Accuracy of COVID tests¶

The results of 100 UCSD Health COVID tests are given below.

Predicted Negative Predicted Positive
Actually Negative TN = 90 ✅ FP = 1 ❌
Actually Positive FN = 8 ❌ TP = 1 ✅
UCSD Health test results

🤔 Question: What is the accuracy of the test?

🙋 Answer: $$\text{accuracy} = \frac{TP + TN}{TP + FP + FN + TN} = \frac{1 + 90}{100} = 0.91$$

  • Followup: At first, the test seems good. But, suppose we build a classifier that predicts that nobody has COVID. What would its accuracy be?
  • Answer to followup: Also 0.91! There is severe class imbalance in the dataset, meaning that most of the data points are in the same class (no COVID). Accuracy doesn't tell the full story.

Recall¶

Predicted Negative Predicted Positive
Actually Negative TN = 90 ✅ FP = 1 ❌
Actually Positive FN = 8 ❌ TP = 1 ✅
UCSD Health test results

🤔 Question: What proportion of individuals who actually have COVID did the test identify?

🙋 Answer: $\frac{1}{1 + 8} = \frac{1}{9} \approx 0.11$

More generally, the recall of a binary classifier is the proportion of actually positive instances that are correctly classified. We'd like this number to be as close to 1 (100%) as possible.

$$\text{recall} = \frac{TP}{\text{# actually positive}} = \frac{TP}{TP + FN}$$

To compute recall, look at the bottom (positive) row of the above confusion matrix.

Recall isn't everything, either!¶

$$\text{recall} = \frac{TP}{TP + FN}$$

🤔 Question: Can you design a "COVID test" with perfect recall?

🙋 Answer: Yes – just predict that everyone has COVID!

Predicted Negative Predicted Positive
Actually Negative TN = 0 ✅ FP = 91 ❌
Actually Positive FN = 0 ❌ TP = 9 ✅
everyone-has-COVID classifier
$$\text{recall} = \frac{TP}{TP + FN} = \frac{9}{9 + 0} = 1$$

Like accuracy, recall on its own is not a perfect metric. Even though the classifier we just created has perfect recall, it has 91 false positives!

Precision¶

Predicted Negative Predicted Positive
Actually Negative TN = 0 ✅ FP = 91 ❌
Actually Positive FN = 0 ❌ TP = 9 ✅
everyone-has-COVID classifier

The precision of a binary classifier is the proportion of predicted positive instances that are correctly classified. We'd like this number to be as close to 1 (100%) as possible.

$$\text{precision} = \frac{TP}{\text{# predicted positive}} = \frac{TP}{TP + FP}$$

To compute precision, look at the right (positive) column of the above confusion matrix.

  • Tip: A good way to remember the difference between precision and recall is that in the denominator for 🅿️recision, both terms have 🅿️ in them (TP and FP).
  • Note that the "everyone-has-COVID" classifier has perfect recall, but a precision of $\frac{9}{9 + 91} = 0.09$, which is quite low.
  • 🚨 Key idea: There is a "tradeoff" between precision and recall. Ideally, you want both to be high. For a particular prediction task, one may be important than the other.

Precision and recall¶

(source)

Precision and recall¶

$$\text{precision} = \frac{TP}{TP + FP} \: \: \: \: \: \: \: \: \text{recall} = \frac{TP}{TP + FN}$$

🤔 Question: When might high precision be more important than high recall?

🙋 Answer: For instance, in deciding whether or not someone committed a crime. Here, false positives are really bad – they mean that an innocent person is charged!

🤔 Question: When might high recall be more important than high precision?

🙋 Answer: For instance, in medical tests. Here, false negatives are really bad – they mean that someone's disease goes undetected!

Discussion Question¶

Consider the confusion matrix shown below.

Predicted Negative Predicted Positive
Actually Negative TN = 22 ✅ FP = 2 ❌
Actually Positive FN = 23 ❌ TP = 18 ✅

What is the accuracy of the above classifier? The precision? The recall?


After calculating all three on your own, click below to see the answers.

Accuracy (22 + 18) / (22 + 2 + 23 + 18) = 40 / 65
Precision 18 / (18 + 2) = 9 / 10
Recall 18 / (18 + 23) = 18 / 41

Example: Tumor malignancy prediction (via logistic regression)¶

Wisconsin breast cancer dataset¶

The Wisconsin breast cancer dataset (WBCD) is a commonly-used dataset for demonstrating binary classification. It is built into sklearn.datasets.

In [2]:
from sklearn.datasets import load_breast_cancer
loaded = load_breast_cancer() # explore the value of `loaded`!
data = loaded['data']
labels = 1 - loaded['target']
cols = loaded['feature_names']
bc = pd.DataFrame(data, columns=cols)
In [3]:
bc.head()
Out[3]:
mean radius mean texture mean perimeter mean area mean smoothness mean compactness mean concavity mean concave points mean symmetry mean fractal dimension ... worst radius worst texture worst perimeter worst area worst smoothness worst compactness worst concavity worst concave points worst symmetry worst fractal dimension
0 17.99 10.38 122.80 1001.0 0.11840 0.27760 0.3001 0.14710 0.2419 0.07871 ... 25.38 17.33 184.60 2019.0 0.1622 0.6656 0.7119 0.2654 0.4601 0.11890
1 20.57 17.77 132.90 1326.0 0.08474 0.07864 0.0869 0.07017 0.1812 0.05667 ... 24.99 23.41 158.80 1956.0 0.1238 0.1866 0.2416 0.1860 0.2750 0.08902
2 19.69 21.25 130.00 1203.0 0.10960 0.15990 0.1974 0.12790 0.2069 0.05999 ... 23.57 25.53 152.50 1709.0 0.1444 0.4245 0.4504 0.2430 0.3613 0.08758
3 11.42 20.38 77.58 386.1 0.14250 0.28390 0.2414 0.10520 0.2597 0.09744 ... 14.91 26.50 98.87 567.7 0.2098 0.8663 0.6869 0.2575 0.6638 0.17300
4 20.29 14.34 135.10 1297.0 0.10030 0.13280 0.1980 0.10430 0.1809 0.05883 ... 22.54 16.67 152.20 1575.0 0.1374 0.2050 0.4000 0.1625 0.2364 0.07678

5 rows × 30 columns

1 stands for "malignant", i.e. cancerous, and 0 stands for "benign", i.e. safe.

In [4]:
labels[:5]
Out[4]:
array([1, 1, 1, 1, 1])
In [5]:
pd.Series(labels).value_counts(normalize=True)
Out[5]:
0    0.627417
1    0.372583
dtype: float64

Our goal is to use the features in bc to predict labels.

Aside: Logistic regression¶

Logistic regression is a linear classification? technique that builds upon linear regression. It models the probability of belonging to class 1, given a feature vector:

$$P(y = 1 | \vec{x}) = \sigma (\underbrace{w_0 + w_1 x^{(1)} + w_2 x^{(2)} + ... + w_d x^{(d)}}_{\text{linear regression model}})$$

Here, $\sigma(t) = \frac{1}{1 + e^{-t}}$ is the sigmoid function; its outputs are between 0 and 1 (which means they can be interpreted as probabilities).

🤔 Question: Suppose our logistic regression model predicts the probability that a tumor is malignant is 0.75. What class do we predict – malignant or benign? What if the predicted probability is 0.3?

🙋 Answer: We have to pick a threshold (e.g. 0.5)!

  • If the predicted probability is above the threshold, we predict malignant (1).
  • Otherwise, we predict benign (0).

Fitting a logistic regression model¶

In [6]:
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
In [7]:
X_train, X_test, y_train, y_test = train_test_split(bc, labels)
In [8]:
clf = LogisticRegression()
clf.fit(X_train, y_train)
Out[8]:
LogisticRegression()

How did clf come up with 1s and 0s?

In [9]:
clf.predict(X_test)
Out[9]:
array([0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0,
       1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0,
       0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1,
       0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0,
       1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1,
       1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1])

It turns out that the predicted labels come from applying a threshold of 0.5 to the predicted probabilities. We can access the predicted probabilities via the predict_proba method:

In [10]:
# [:, 1] refers to the predicted probabilities for class 1
clf.predict_proba(X_test)[:, 1]
Out[10]:
array([4.79267883e-01, 2.67827969e-04, 4.76852669e-03, 8.70327442e-03,
       1.21863170e-03, 3.70160949e-03, 3.83147967e-01, 9.99999943e-01,
       4.66204175e-03, 4.97949135e-02, 9.78836837e-01, 5.25592813e-02,
       1.99357043e-02, 1.00000000e+00, 9.99999999e-01, 1.68184647e-01,
       1.32004744e-03, 5.97235870e-02, 6.10571513e-04, 9.94544173e-01,
       1.58385001e-02, 5.96271996e-03, 9.87646468e-01, 9.99999308e-01,
       7.45093008e-02, 9.99999635e-01, 1.34666734e-03, 3.58815186e-03,
       7.25792681e-04, 3.00964858e-02, 7.43892951e-03, 3.90124284e-01,
       3.53632205e-02, 1.83998979e-02, 4.07877069e-02, 4.82118150e-01,
       7.97402959e-02, 5.45118223e-01, 5.39598523e-02, 1.00000000e+00,
       9.99999847e-01, 8.69193761e-04, 1.81118232e-03, 1.40103764e-02,
       8.76509342e-03, 8.51826940e-02, 3.05640094e-04, 9.07055614e-01,
       9.99996854e-01, 1.10164806e-03, 9.99960769e-01, 8.39738072e-04,
       9.99853446e-01, 7.33644323e-03, 7.27749494e-04, 9.99978185e-01,
       9.97342100e-01, 7.33400223e-04, 7.01243148e-02, 1.62988050e-01,
       2.05537549e-01, 2.31460636e-03, 1.17678756e-02, 3.73694738e-02,
       6.55322443e-02, 1.91015031e-02, 9.98132639e-01, 1.79263594e-02,
       9.98735664e-01, 9.99999810e-01, 2.87922004e-03, 3.76868417e-01,
       1.48930825e-02, 3.94710864e-03, 3.11891813e-03, 1.16008076e-02,
       2.43914080e-03, 1.79206056e-02, 1.00000000e+00, 9.99998610e-01,
       4.29458076e-04, 7.37391819e-03, 8.22645940e-03, 1.00000000e+00,
       9.40750871e-01, 9.91048725e-01, 5.32866151e-01, 1.00000000e+00,
       3.44629254e-01, 6.87601229e-01, 3.01413426e-02, 9.97183964e-01,
       9.02357017e-01, 2.28039096e-02, 3.34593997e-02, 1.62305385e-02,
       9.86350687e-03, 9.99838343e-01, 9.99177885e-01, 3.77368576e-03,
       1.00000000e+00, 9.99999999e-01, 1.00000000e+00, 9.69035937e-03,
       4.88720495e-01, 8.66520781e-03, 9.09772555e-04, 3.36368641e-02,
       6.44916191e-03, 6.21002898e-02, 9.35790904e-01, 9.99989435e-01,
       3.55597734e-03, 2.25364520e-02, 5.73787846e-03, 2.52514802e-02,
       9.75565074e-01, 1.50782627e-03, 1.85820922e-01, 2.03491596e-03,
       8.19353870e-03, 4.99770941e-02, 2.83695169e-03, 1.40025315e-01,
       5.60047584e-03, 4.13991392e-03, 9.99999942e-01, 6.34309633e-02,
       1.00997231e-02, 2.86350505e-02, 1.00000000e+00, 1.00000000e+00,
       9.99999968e-01, 2.37308315e-02, 9.99989669e-01, 2.25716024e-02,
       7.61438549e-03, 2.60757316e-01, 2.37460631e-03, 9.99999639e-01,
       4.42059121e-02, 9.99830667e-01, 7.34985866e-01])

Note that our model still has $w^*$s:

In [11]:
clf.intercept_
Out[11]:
array([-0.22454193])
In [12]:
clf.coef_
Out[12]:
array([[-1.17201122, -0.47956959, -0.05204137,  0.00274439,  0.04403017,
         0.21280417,  0.2934432 ,  0.12392108,  0.06314264,  0.01314701,
        -0.06643895, -0.56592992, -0.23312689,  0.12693186,  0.0031996 ,
         0.04585577,  0.05894403,  0.01518868,  0.01790763,  0.00374143,
        -1.35418505,  0.53133132,  0.158254  ,  0.02015834,  0.07873998,
         0.67181916,  0.81639231,  0.23801492,  0.20903196,  0.06293511]])

Evaluating our model¶

Let's see how well our model does on the test set.

In [13]:
from sklearn import metrics
In [14]:
y_pred = clf.predict(X_test)
In [15]:
metrics.accuracy_score(y_test, y_pred)
Out[15]:
0.9300699300699301
In [16]:
metrics.precision_score(y_test, y_pred)
Out[16]:
0.9782608695652174
In [17]:
metrics.recall_score(y_test, y_pred)
Out[17]:
0.8333333333333334

Which metric is more important for this task – precision or recall?

In [18]:
metrics.confusion_matrix(y_test, y_pred)
Out[18]:
array([[88,  1],
       [ 9, 45]])
In [19]:
metrics.plot_confusion_matrix(clf, X_test, y_test)
Out[19]:
<sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay at 0x7fab2003f460>

What if we choose a different threshold?¶

🤔 Question: Suppose we choose a threshold higher than 0.5. What will happen to our model's precision and recall?

🙋 Answer: Precision will increase, while recall will decrease*.

  • If the "bar" is higher to predict 1, then we will have fewer false positives.
  • The denominator in $\text{precision} = \frac{TP}{TP + FP}$ will get smaller, and so precision will increase.
  • However, the number of false negatives will increase, as we are being more "strict" about what we classify as positive, and so $\text{recall} = \frac{TP}{TP + FN}$ will decrease.
  • *It is possible for either or both to stay the same, if changing the threshold slightly (e.g. from 0.5 to 0.500001) doesn't change any predictions.

Similarly, if we decrease our threshold, our model's precision will decrease, while its recall will increase.

Trying several thresholds¶

The classification threshold is not actually a hyperparameter of LogisticRegression, because the threshold doesn't change the coefficients ($w^*$s) of the logistic regression model itself (see this article for more details).

As such, if we want to imagine how our predicted classes would change with thresholds other than 0.5, we need to manually threshold.

In [20]:
thresholds = np.arange(0, 1.01, 0.01)
precisions = np.array([])
recalls = np.array([])

for t in thresholds:
    y_pred = clf.predict_proba(X_test)[:, 1] >= t
    precisions = np.append(precisions, metrics.precision_score(y_test, y_pred))
    recalls = np.append(recalls, metrics.recall_score(y_test, y_pred))

Let's visualize the results in plotly, which is interactive.

In [21]:
px.line(x=thresholds, y=precisions,
        labels={'x': 'Threshold', 'y': 'Precision'}, title='Precision vs. Threshold', width=1000, height=600,
        template=TEMPLATE)
In [22]:
px.line(x=thresholds, y=recalls, 
        labels={'x': 'Threshold', 'y': 'Recall'}, title='Recall vs. Threshold', width=1000, height=600,
        template=TEMPLATE)
In [23]:
px.line(x=recalls, y=precisions, hover_name=thresholds, 
        labels={'x': 'Recall', 'y': 'Precision'}, title='Precision vs. Recall',
        template=TEMPLATE)

The above curve is called a precision-recall (or PR) curve.

🤔 Question: Based on the PR curve above, what threshold would you choose?

Combining precision and recall¶

If we care equally about a model's precision $PR$ and recall $RE$, we can combine the two using a single metric called the F1-score:

$$\text{F1-score} = \text{harmonic mean}(PR, RE) = 2\frac{PR \cdot RE}{PR + RE}$$
In [24]:
pr = metrics.precision_score(y_test, clf.predict(X_test))
re = metrics.recall_score(y_test, clf.predict(X_test))

2 * pr * re / (pr + re)
Out[24]:
0.9
In [25]:
metrics.f1_score(y_test, clf.predict(X_test))
Out[25]:
0.9

Both F1-score and accuracy are overall measures of a binary classifier's performance. But remember, accuracy is misleading in the presence of class imbalance, and doesn't take into account the kinds of errors the classifier makes.

In [26]:
metrics.accuracy_score(y_test, clf.predict(X_test))
Out[26]:
0.9300699300699301

Other evaluation metrics for binary classifiers¶

We just scratched the surface! This excellent table from Wikipedia summarizes the many other metrics that exist.

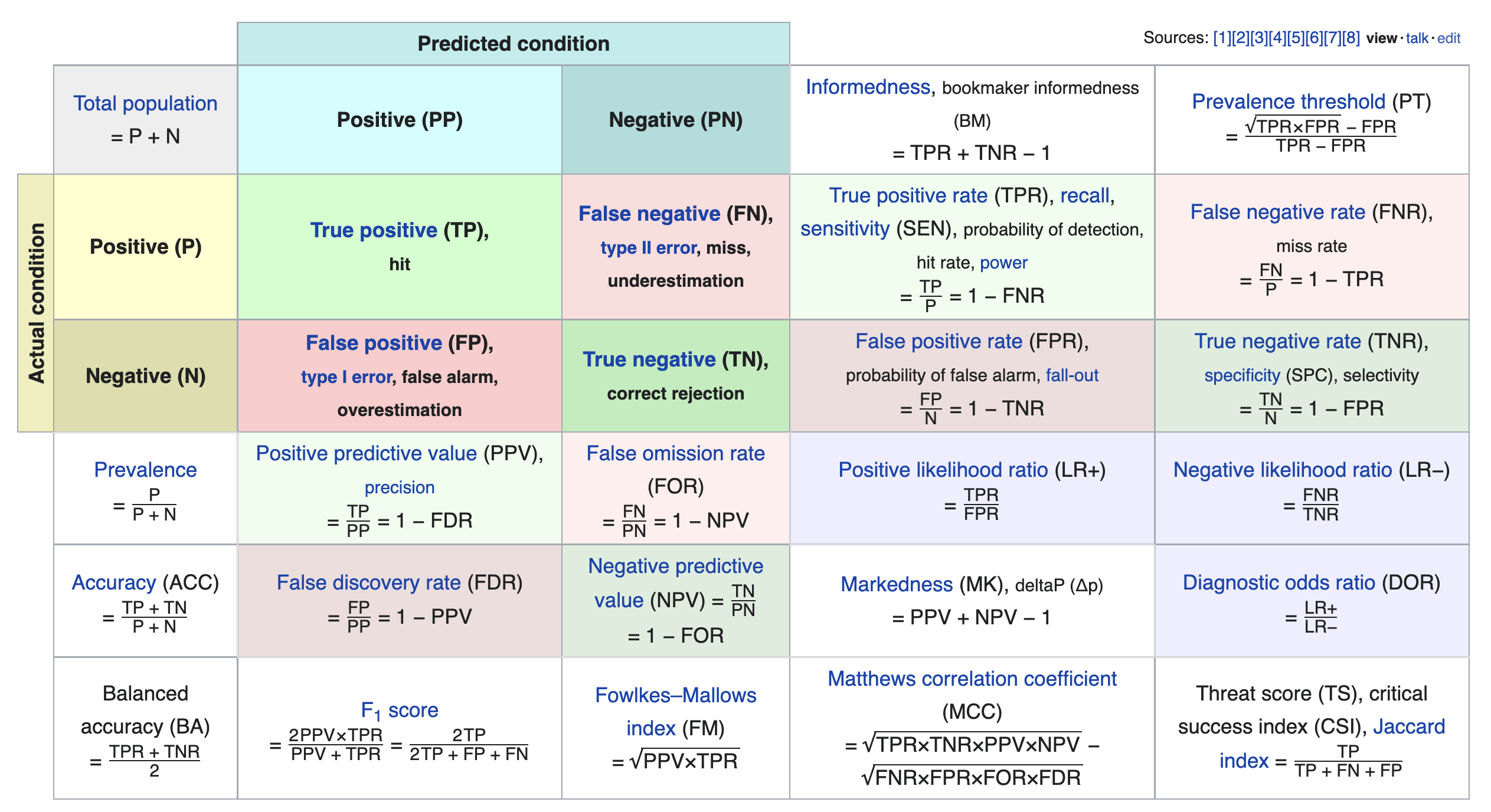
If you're interested in exploring further, a good next metric to look at is true negative rate (i.e. specificity), which is the analogue of recall for true negatives.

Summary, next time¶

Summary¶

  • Accuracy alone is not always a meaningful representation of a classifier's quality, particularly when the classes are imbalanced.
    • Precision and recall are classifier evaluation metrics that consider the types of errors being made.
    • There is a "tradeoff" between precision and recall. One may be more important than the other, depending on the task.
  • A logistic regression model makes classifications by first predicting a probability and then thresholding that probability.
    • The default threshold is 0.5; by moving the threshold, we change the balance between precision and recall.

Next time¶

Quantifying the fairness of predictive models. Conclusion.