import pandas as pd
import numpy as np
import os

import seaborn as sns
import plotly.express as px
import plotly.figure_factory as ff
import plotly.graph_objects as go
pd.options.plotting.backend = 'plotly'

# Used for plotting examples.
def create_kde_plotly(df, group_col, group1, group2, vals_col, title=''):
    fig = ff.create_distplot(
        hist_data=[df.loc[df[group_col] == group1, vals_col], df.loc[df[group_col] == group2, vals_col]],
        group_labels=[group1, group2],
        show_rug=False, show_hist=False,
        colors=['#ef553b', '#636efb'],
    )
    return fig.update_layout(title=title)

Lecture 12 – Identifying Missingness Mechanisms

DSC 80, Winter 2023

Announcements

• Lab 4 is due tonight at 11:59PM.
  • See this post on Ed for clarifications.
• Project 2 is due on Thursday, February 9th at 11:59PM.
• The Grade Report on Gradescope now contains scores and slip days through Lab 3.
• Remember to run conda activate dsc80 before working on assignments!

Agenda

• Review and discussion: missingness mechanisms.
• Deciding between MCAR and MAR using permutation tests.
• A new test statistic for permutation tests: the Kolmogorov-Smirnov statistic.

Missingness mechanisms

Flowchart

A good strategy is to assess missingness in the following order.

Missing by design (MD)

Can I determine the missing value exactly by looking at the other columns? 🤔 $$\downarrow$$

Not missing at random (NMAR)

Is there a good reason why the missingness depends on the values themselves? 🤔 $$\downarrow$$

Missing at random (MAR)

Do other columns tell me anything about the likelihood that a value is missing? 🤔 $$\downarrow$$

Missing completely at random (MCAR) The missingness must not depend on other columns or the values themselves. 😄

Discussion Question

In each of the following examples, decide whether the missing data are likely to be MD, NMAR, MAR, or MCAR:

• A table for a medical study has columns for 'gender' and 'age'. 'age' has missing values.
• Measurements from the Hubble Space Telescope are dropped during transmission.
• A table has a single column, 'self-reported education level', which contains missing values.
• A table of grades contains three columns, 'Version 1', 'Version 2', and 'Version 3'. $\frac{2}{3}$ of the entries in the table are NaN.

Why do we care again?

• If a dataset contains missing values, it is likely not an accurate picture of the data generating process.
• By identifying missingness mechanisms, we can best fill in missing values, to gain a better understanding of the DGP.

Formal definitions

We won't spend much time on these in lecture, but you may find them helpful.

Formal definition: MCAR

Suppose we have:

• A dataset $Y$ with observed values $Y_{obs}$ and missing values $Y_{mis}$.
• A parameter $\psi$ that represents all relevant information that is not part of the dataset.

Data is missing completely at random (MCAR) if

$$\text{P}(\text{data is present} \: | \: Y_{obs}, Y_{mis}, \psi) = \text{P}(\text{data is present} \: | \: \psi)$$

That is, adding information about the dataset doesn't change the likelihood data is missing!

Formal definition: MAR

Suppose we have:

• A dataset $Y$ with observed values $Y_{obs}$ and missing values $Y_{mis}$.
• A parameter $\psi$ that represents all relevant information that is not part of the dataset.

Data is missing at random (MCAR) if

$$\text{P}(\text{data is present} \: | \: Y_{obs}, Y_{mis}, \psi) = \text{P}(\text{data is present} \: | \: Y_{obs}, \psi)$$

That is, MAR data is actually MCAR, conditional on $Y_{obs}$.

Formal definition: NMAR

Suppose we have:

• A dataset $Y$ with observed values $Y_{obs}$ and missing values $Y_{mis}$.
• A parameter $\psi$ that represents all relevant information that is not part of the dataset.

Data is not missing at random (NMAR) if

$$\text{P}(\text{data is present} \: | \: Y_{obs}, Y_{mis}, \psi)$$

cannot be simplified. That is, in NMAR data, missingness is dependent on the missing value itself.

Assessing missingness through data

Assessing missingness through data

• Suppose I believe that the missingness mechanism of a column is NMAR, MAR, or MCAR.
  • I've ruled out missing by design (a good first step).
• Can I check whether this is true, by looking at the data?

Assessing NMAR

• We can't determine if data is NMAR just by looking at the data, as whether or not data is NMAR depends on the unobserved data.
• To establish if data is NMAR, we must:
  • reason about the data generating process, or
  • collect more data.

• Example: Consider a dataset of survey data of students' self-reported happiness. The data contains PIDs and happiness scores; nothing else. Some happiness scores are missing. Are happiness scores likely NMAR?

Assessing MAR

• Data are MAR if the missingness only depends on observed data.
• After reasoning about the data generating process, if you establish that data is not NMAR, then it must be either MAR or MCAR.
• The more columns we have in our dataset, the "weaker the NMAR effect" is.
  • Adding more columns -> controlling for more variables -> moving from NMAR to MAR.
  • Example: With no other columns, income in a census is NMAR. But once we look at location, education, and occupation, incomes are closer to being MAR.

Deciding between MCAR and MAR

• For data to be MCAR, the chance that values are missing should not depend on any other column or the values themselves.

• Example: Consider a dataset of phones, in which we store the screen size and price of each phone. Some prices are missing.

Phone	Screen Size	Price
iPhone 14	6.06	999
Galaxy Z Fold 4	7.6	NaN
OnePlus 9 Pro	6.7	799
iPhone 13 Pro Max	6.68	NaN

• If prices are MCAR, then the distribution of screen size should be the same for:
  • phones whose prices are missing, and
  • phones whose prices aren't missing.

• We can use a permutation test to decide between MAR and MCAR! We are asking the question, did these two samples come from the same underlying distribution?

Deciding between MCAR and MAR

Suppose you have a DataFrame with columns named $\text{col}_1$, $\text{col}_2$, ..., $\text{col}_k$, and want to test whether values in $\text{col}_X$ are MCAR. To test whether $\text{col}_X$'s missingness is independent of all other columns in the DataFrame:

For $i = 1, 2, ..., k$, where $i \neq X$:

• Look at the distribution of $\text{col}_i$ when $\text{col}_X$ is missing.

• Look at the distribution of $\text{col}_i$ when $\text{col}_X$ is not missing.

• Check if these two distributions are the same. (What do we mean by "the same"?)

• If so, then $\text{col}_X$'s missingness doesn't depend on $\text{col}_i$.

• If not, then $\text{col}_X$ is MAR dependent on $\text{col}_i$.

If all pairs of distribution were the same, then $\text{col}_X$ is MCAR.

Example: Heights

• Let's load in Galton's dataset containing the heights of adult children and their parents (which you may have seen in DSC 10).
• The dataset does not contain any missing values – we will artifically introduce missing values such that the values are MCAR, for illustration.

heights = pd.read_csv('data/midparent.csv')
heights = heights.rename(columns={'childHeight': 'child'})
heights = heights[['father', 'mother', 'gender', 'child']]
heights.head()

	father	mother	gender	child
0	78.5	67.0	male	73.2
1	78.5	67.0	female	69.2
2	78.5	67.0	female	69.0
3	78.5	67.0	female	69.0
4	75.5	66.5	male	73.5

Proof that there aren't currently any missing values in heights:

heights.isna().sum()

father    0
mother    0
gender    0
child     0
dtype: int64

We have three numerical columns – 'father', 'mother', and 'child'. Let's visualize them simultaneously.

fig = px.scatter_matrix(heights.drop(columns=['gender']))
fig

/Users/surajrampure/opt/anaconda3/lib/python3.9/site-packages/plotly/express/_core.py:279: FutureWarning: iteritems is deprecated and will be removed in a future version. Use .items instead.
  dims = [

Simulating MCAR data

• We will make 'child' MCAR by taking a random subset of heights and setting the corresponding 'child' heights to np.NaN.
• This is equivalent to flipping a (biased) coin for each row.
  • If heads, we delete the 'child' height.
• You will not do this in practice!

np.random.seed(42) # So that we get the same results each time (for lecture).

heights_mcar = heights.copy()
idx = heights_mcar.sample(frac=0.3).index
heights_mcar.loc[idx, 'child'] = np.NaN

heights_mcar.head(10)

	father	mother	gender	child
0	78.5	67.0	male	73.2
1	78.5	67.0	female	69.2
2	78.5	67.0	female	NaN
3	78.5	67.0	female	69.0
4	75.5	66.5	male	73.5
5	75.5	66.5	male	NaN
6	75.5	66.5	female	65.5
7	75.5	66.5	female	NaN
8	75.0	64.0	male	71.0
9	75.0	64.0	female	68.0

heights_mcar.isna().mean()

father    0.000000
mother    0.000000
gender    0.000000
child     0.299786
dtype: float64

Aside: Why is the value for 'child' in the above Series not exactly 0.3?

Verifying that child heights are MCAR in heights_mcar

• Each row of heights_mcar belongs to one of two groups:
  • Group 1: 'child' is missing.
  • Group 2: 'child' is not missing.

heights_mcar['child_missing'] = heights_mcar['child'].isna()
heights_mcar.head()

	father	mother	gender	child	child_missing
0	78.5	67.0	male	73.2	False
1	78.5	67.0	female	69.2	False
2	78.5	67.0	female	NaN	True
3	78.5	67.0	female	69.0	False
4	75.5	66.5	male	73.5	False

• We need to look at the distributions of every other column – 'gender', 'mother', and 'father' – separately for these two groups, and check to see if they are similar.

Comparing null and non-null 'child' distributions for 'gender'

gender_dist = (
    heights_mcar
    .assign(child_missing=heights_mcar['child'].isna())
    .pivot_table(index='gender', columns='child_missing', aggfunc='size')
)

# Added just to make the resulting pivot table easier to read.
gender_dist.columns = ['child_missing = False', 'child_missing = True']

gender_dist = gender_dist / gender_dist.sum()
gender_dist

	child_missing = False	child_missing = True
gender
female	0.487768	0.478571
male	0.512232	0.521429

• Note that here, each column is a separate distribution that adds to 1.

• The two columns look similar, which is evidence that 'child''s missingness does not depend on 'gender'.
  • Knowing that the child is 'female' doesn't make it any more or less likely that their height is missing than knowing if the child is 'male'.

Comparing null and non-null 'child' distributions for 'gender'

• In the previous slide, we saw that the distribution of 'gender' is similar whether or not 'child' is missing.

• To make precise what we mean by "similar", we can run a permutation test. We are comparing two distributions:
  1. The distribution of 'gender' when 'child' is missing.
  2. The distribution of 'gender' when 'child' is not missing.

• What test statistic do we use to compare categorical distributions?

gender_dist.plot(kind='barh', title='Gender by Missingness of Child Height', barmode='group')

To measure the "distance" between two categorical distributions, we use the total variation distance.

Note that with only two categories, the TVD is the same as the absolute difference in proportions for either category.

Simulation

The code to run our simulation largely looks the same as in previous permutation tests.

n_repetitions = 500
shuffled = heights_mcar.copy()

tvds = []
for _ in range(n_repetitions):
    
    # Shuffling genders. 
    # Note that we are assigning back to the same DataFrame for performance reasons; 
    # see https://dsc80.com/resources/lectures/lec11/lec11-fast-permutation-tests.html.
    shuffled['gender'] = np.random.permutation(shuffled['gender'])
    
    # Computing and storing the TVD.
    pivoted = (
        shuffled
        .pivot_table(index='gender', columns='child_missing', aggfunc='size')
        .apply(lambda x: x / x.sum())
    )
    
    tvd = pivoted.diff(axis=1).iloc[:, -1].abs().sum() / 2
    tvds.append(tvd)

observed_tvd = gender_dist.diff(axis=1).iloc[:, -1].abs().sum() / 2
observed_tvd

0.009196155526430771

Results

fig = px.histogram(pd.DataFrame(tvds), x=0, nbins=50, histnorm='probability', 
                   title='Empirical Distribution of the TVD')
fig.add_vline(x=observed_tvd, line_color='red')
fig.add_annotation(text=f'<span style="color:red">Observed TVD = {round(observed_tvd, 2)}</span>',
                   x=2.3 * observed_tvd, showarrow=False, y=0.16)
fig.update_layout(yaxis_range=[0, 0.2])

np.mean(np.array(tvds) >= observed_tvd)

0.838

• We fail to reject the null.
• Recall, the null stated that the distribution of 'gender' when 'child' is missing is the same as the distribution of 'gender' when 'child' is not missing.
• Hence, we conclude that the missingness in the 'child' column is not dependent on 'gender'.

Comparing null and non-null 'child' distributions for 'father'

• We again must compare two distributions:
  1. The distribution of 'father' when 'child' is missing.
  2. The distribution of 'father' when 'child' is not missing.

• If the distributions are similar, we conclude that the missingness of 'child' is not dependent on the height of the 'father'.

• We can again use a permutation test.

px.histogram(heights_mcar, x='father', color='child_missing', histnorm='probability', marginal='box',
             title="Father's Height by Missingness of Child Height", barmode='overlay', opacity=0.7)

We can visualize numerical distributions with histograms, or with kernel density estimates. (See the definition of create_kde_plotly at the top of the notebook if you're curious as to how these are created.)

create_kde_plotly(heights_mcar, 'child_missing', True, False, 'father', 
                  "Father's Height by Missingness of Child Height")

Concluding that 'child' is MCAR

• We need to run three permutation tests – one for each column in heights_mcar other than 'child'.

• For every other column, if we fail to reject the null that the distribution of the column when 'child' is missing is the same as the distribution of the column when 'child' is not missing, then we can conclude 'child' is MCAR.
  • In such a case, its missingness is not tied to any other columns.
  • For instance, children with shorter fathers are not any more likely to have missing heights than children with taller fathers.

Simulating MAR data

Now, we will make 'child' heights MAR by deleting 'child' heights according to a random procedure that depends on other columns.

np.random.seed(42) # So that we get the same results each time (for lecture).

def make_missing(r):
    rand = np.random.uniform() # Random real number between 0 and 1.
    if r['father'] > 72 and rand < 0.5:
        return np.NaN
    elif r['gender'] == 'female' and rand < 0.3:
        return np.NaN
    else:
        return r['child']
    
heights_mar = heights.copy()
heights_mar['child'] = heights_mar.apply(make_missing, axis=1)
heights_mar['child_missing'] = heights_mar['child'].isna()

heights_mar.head()

	father	mother	gender	child	child_missing
0	78.5	67.0	male	NaN	True
1	78.5	67.0	female	69.2	False
2	78.5	67.0	female	69.0	False
3	78.5	67.0	female	69.0	False
4	75.5	66.5	male	NaN	True

Comparing null and non-null 'child' distributions for 'gender', again

This time, the distribution of 'gender' in the two groups is very different.

gender_dist = (
    heights_mar
    .assign(child_missing=heights_mar['child'].isna())
    .pivot_table(index='gender', columns='child_missing', aggfunc='size')
)

# Added just to make the resulting pivot table easier to read.
gender_dist.columns = ['child_missing = False', 'child_missing = True']

gender_dist = gender_dist / gender_dist.sum()
gender_dist

	child_missing = False	child_missing = True
gender
female	0.397386	0.881657
male	0.602614	0.118343

gender_dist.plot(kind='barh', title='Gender by Missingness of Child Height', barmode='group')

• Question: If we take the average of the non-null 'child' heights in the dataset with missing values, will it be less than or greater than the average 'child' height in the full dataset?

• Answer:
  • 'child' heights tend to be missing much more frequently when the child is 'female'.
  • Adult females tend to be shorter than adult males on average.
  • Thus, the average 'child' height in the dataset with missing values will be greater than the average 'child' height in the full dataset.

# When child heights are MAR:
heights_mar['child'].mean()

67.10339869281046

# When child heights are not missing:
heights['child'].mean()

66.74593147751605

# When child heights are MCAR:
heights_mcar['child'].mean()

66.7256880733945

Comparing null and non-null 'child' distributions for 'father', again

create_kde_plotly(heights_mar, 'child_missing', True, False, 'father', 
                  "Father's Height by Missingness of Child Height")

• The above two distributions look quite different.
  • This is because we artificially created missingness in the dataset in a way that depended on 'father' and 'gender'.

• However, their difference in means is small:

heights_mar.groupby('child_missing')['father'].mean().diff().iloc[-1]

1.0055466604787853

• If we ran a permutation test with the difference in means as our test statistic, we would fail to reject the null.
  • Using just the difference in means, it is hard to tell these two distributions apart.

The Kolmogorov-Smirnov test statistic

Recap: Permutation tests

• Permutation tests help decide whether two samples look like they were drawn from the same population distribution.
• In a permutation test, we simulate data under the null by shuffling either group labels or numerical features.
  • In effect, this randomly assigns individuals to groups.
• If the two distributions are quantitative (numerical), we use as our test statistic the difference in group means or medians.
• If the two distributions are qualitative (categorical), we use as our test statistic the total variation distance (TVD).

Difference in means

The difference in means works well in some cases. Let's look at one such case.

Below, we artificially generate two numerical datasets.

np.random.seed(42) # So that we get the same results each time (for lecture).

N = 1000 # Number of samples for each distribution.

# Distribution 'A'.
distr1 = pd.Series(np.random.normal(0, 1, size=N//2))

# Distribution 'B'.
distr2 = pd.Series(np.random.normal(3, 1, size=N//2))

data = pd.concat([distr1, distr2], axis=1, keys=['A', 'B']).unstack().reset_index().drop('level_1', axis=1)
data = data.rename(columns={'level_0': 'group', 0: 'data'})

meanA, meanB = data.groupby('group')['data'].mean().round(7).tolist()
create_kde_plotly(data, 'group', 'A', 'B', 'data', f'mean of A: {meanA}<br>mean of B: {meanB}')

Discussion Question

• So far, we have used the difference in means as our test statistic in quantitative permutation tests.
• We've concluded that two distributions were likely different if their means were different.
• Can you think of two different distributions that have the same mean? 🤔

Different distributions with the same mean

Let's generate two distributions that look very different but have the same mean.

np.random.seed(42) # So that we get the same results each time (for lecture).

N = 1000 # Number of samples for each distribution.

# Distribution 'A'.
a = pd.Series(np.random.normal(0, 1, size=N//2))
b = pd.Series(np.random.normal(4, 1, size=N//2))
distr1 = pd.concat([a,b], ignore_index=True)

# Distribution 'B'.
distr2 = pd.Series(np.random.normal(distr1.mean(), distr1.std(), size=N))

data = pd.concat([distr1, distr2], axis=1, keys=['A', 'B']).unstack().reset_index().drop('level_1', axis=1)
data = data.rename(columns={'level_0': 'group', 0: 'data'})

meanA, meanB = data.groupby('group')['data'].mean().round(7).tolist()
create_kde_plotly(data, 'group', 'A', 'B', 'data', f'mean of A: {meanA}<br>mean of B: {meanB}')

In this case, if we use the difference in means as our test statistic in a permutation test, we will fail to reject the null that the two distributions are different.

n_repetitions = 500
shuffled = data.copy()

diff_means = []
for _ in range(n_repetitions):
    
    # Shuffling the values, while keeping the group labels in place.
    shuffled['data'] = np.random.permutation(shuffled['data'])
    
    # Computing and storing the absolute difference in means.
    diff_mean = shuffled.groupby('group')['data'].mean().diff().abs().iloc[-1]
    diff_means.append(diff_mean)
    
diff_means[:10]

[0.06814385394584033,
 0.010122359182524576,
 0.2002163697731203,
 0.2428154903924331,
 0.010075853494653675,
 0.07500611481190367,
 0.02273396310350906,
 0.0016829212124784831,
 0.015376481518938778,
 0.08595787219948381]

observed_diff = data.groupby('group')['data'].mean().diff().abs().iloc[-1]
fig = px.histogram(pd.DataFrame(diff_means), x=0, nbins=50, histnorm='probability', 
                   title='Empirical Distribution of the Absolute Difference in Means')
fig.add_vline(x=observed_diff, line_color='red')
fig.add_annotation(text=f'<span style="color:red">Observed Absolute Difference in Means = {round(observed_diff, 2)}</span>',
                   x=1.45 * observed_diff, showarrow=False, y=0.07)

# The computed p-value is fairly large.
np.mean(np.array(diff_means) >= observed_diff)

0.108

Telling quantitative distributions apart

• The difference in means only works as a test statistic in permutation tests if the two distributions have similar shapes.
  • It tests to see if one is a shifted version of the other.

• We need a better test statistic to differentiate between quantitative distributions with different shapes.

• In other words, we need a distance metric between quantitative distributions.
  • The TVD is a distance metric between categorical distributions.

create_kde_plotly(data, 'group', 'A', 'B', 'data', f'mean of A: {meanA}<br>mean of B: {meanB}')

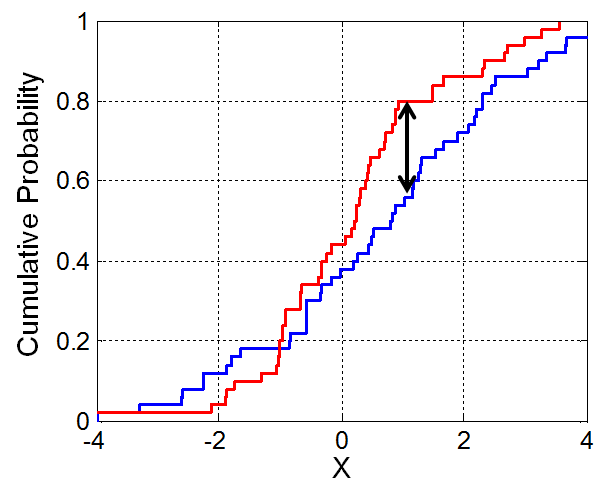
The Kolmogorov-Smirnov test statistic

• The K-S test statistic measures the similarity between two distributions.
• It is defined in terms of the cumulative distribution function (CDF) of a given distribution.
  • If $f(x)$ is a distribution, then the CDF $F(x)$ is the proportion of values in distribution $f$ that are less than or equal to $x$.
• The K-S statistic is roughly defined as the largest difference between two CDFs.

Aside: cumulative distribution functions

Let's look at the CDFs of our two synthetic distributions.

# Think about what this function is doing!
def create_cdf(group):
    return data.loc[data['group'] == group, 'data'].value_counts(normalize=True).sort_index().cumsum()

fig = go.Figure()

fig.add_trace(
    go.Scatter(x=create_cdf('A').index, y=create_cdf('A'), name='CDF of A')
)

fig.add_trace(
    go.Scatter(x=create_cdf('B').index, y=create_cdf('B'), name='CDF of B')
)

fig.update_layout(title='CDFs of A and B')

The K-S statistic in Python

Fortunately, we don't need to calculate the K-S statistic ourselves! Python can do it for us (and you can use this pre-built version in all assignments).

from scipy.stats import ks_2samp

ks_2samp?

observed_ks = ks_2samp(data.loc[data['group'] == 'A', 'data'], data.loc[data['group'] == 'B', 'data']).statistic
observed_ks

0.14

We don't know if this number is big or small. We need to run a permutation test!

n_repetitions = 500
shuffled = data.copy()

ks_stats = []
for _ in range(n_repetitions):
    
    # Shuffling the data.
    shuffled['data'] = np.random.permutation(shuffled['data'])
    
    # Computing and storing the K-S statistic.
    groups = shuffled.groupby('group')['data']
    ks_stat = ks_2samp(groups.get_group('A'), groups.get_group('B')).statistic
    ks_stats.append(ks_stat)
    
ks_stats[:10]

[0.037, 0.048, 0.04, 0.068, 0.045, 0.04, 0.042, 0.052, 0.019, 0.029]

fig = px.histogram(pd.DataFrame(ks_stats), x=0, nbins=50, histnorm='probability', 
                   title='Empirical Distribution of the K-S Statistic')
fig.add_vline(x=observed_ks, line_color='red')
fig.add_annotation(text=f'<span style="color:red">Observed KS = {round(observed_ks, 2)}</span>',
                   x=0.85 * observed_ks, showarrow=False, y=0.16)

fig.update_layout(xaxis_range=[0, 0.2])
fig.update_layout(yaxis_range=[0, 0.2])

np.mean(np.array(ks_stats) >= observed_ks)

0.0

We were able to differentiate between the two distributions using the K-S test statistic!

ks_2samp

• scipy.stats.ks_2samp actually returns both the statistic and a p-value.
• The p-value is calculated using the permutation test we just performed!

ks_2samp(data.loc[data['group'] == 'A', 'data'], data.loc[data['group'] == 'B', 'data'])

KstestResult(statistic=0.14, pvalue=5.822752148022591e-09)

Summary, next time

Summary

• We can use permutation tests to verify if a column is MAR vs. MCAR.
  • Create two groups: one where values in a column are missing, and another where values in a column aren't missing.
  • To test the missingness of column X:
    • For every other column, test the null hypothesis "the distribution of (other column) is the same when column X is missing and when column X is not missing."
    • If you fail to reject the null, then column X's missingness does not depend on (other column).
    • If you reject the null, then column X is MAR dependent on (other column).
    • If you fail to reject the null for all other columns, then column X is MCAR!
• To compare two distributions in a permutation test, the choice of test statistic depends on the type and shape of the distributions:
  • If the two distributions are qualitative (categorical), use the total variation distance (TVD).
  • If the two distributions are quantitative (numerical) and look like shifted versions of the same basic shape, use the difference in group means or medians.
  • If the two distributions are quantitative (numerical) and are centered in the same location but have different shapes, use the Kolmogorov-Smirnov statistic.