- The dot product also has a geometric interpretation. If $|\vec{a}|$ and $|\vec{b}|$ are the $L_2$ norms (lengths) of $\vec{a}$ and $\vec{b}$, and $\theta$ is the angle between $\vec{a}$ and $\vec{b}$, then:
 (source)
(source)import pandas as pd
import numpy as np
import re
from IPython.display import YouTubeVideo
import util
salaries = pd.read_csv('https://transcal.s3.amazonaws.com/public/export/san-diego-2021.csv')
util.anonymize_names(salaries)
jobtitles = salaries['Job Title']
jobtitles = jobtitles[jobtitles.notna()]
jobtitles = (
jobtitles
.str.lower()
.str.replace(r'\bto\b|\bthe\b|\bfor\b', '', regex=True)
.str.replace('[^A-Za-z0-9 ]', ' ', regex=True)
.str.replace(' +', ' ', regex=True) # ' +' matches 1 or more occurrences of a space.
.str.strip() # Removes leading/trailing spaces if present.
)
unique_words = pd.Series(jobtitles.str.split().sum()).value_counts()
# Created using a dictionary to avoid a "DataFrame is highly fragmented" warning.
counts_dict = {}
for word in unique_words.index:
re_pat = fr'\b{word}\b'
counts_dict[word] = jobtitles.str.count(re_pat).astype(int).tolist()
counts_df = pd.DataFrame(counts_dict).set_index(jobtitles)
Recall, we're working with a (real) dataset of salary data for all San Diego city employees.
jobtitles
0 city attorney
1 mayor
2 investment officer
3 police officer
4 independent budget analyst
...
12300 recreation leader i
12301 fire fighter ii
12302 fire captain
12303 fleet repair supervisor
12304 fire engineer
Name: Job Title, Length: 12303, dtype: object
Our goal is to quantify how similar two job titles are; so far, our metric has been the number of shared words between the two titles.
Let's create a "counts" matrix, such that:
title and column word is the number of occurrences of word in title.counts_df
| officer | ii | police | i | assistant | fire | engineer | civil | iii | technician | ... | estate | stores | assets | treasurer | risk | security | geologist | utilities | gardener | principle | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Job Title | |||||||||||||||||||||
| city attorney | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| mayor | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| investment officer | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| police officer | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| independent budget analyst | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| recreation leader i | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| fire fighter ii | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| fire captain | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| fleet repair supervisor | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| fire engineer | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
12303 rows × 327 columns
'deputy fire chief'?¶counts_df, which contains a row vector for each job title.To start, let's compare the row vectors for 'deputy fire chief' and 'fire battalion chief'.
dfc = counts_df.loc['deputy fire chief'].iloc[0]
dfc
officer 0
ii 0
police 0
i 0
assistant 0
..
security 0
geologist 0
utilities 0
gardener 0
principle 0
Name: deputy fire chief, Length: 327, dtype: int64
fbc = counts_df.loc['fire battalion chief'].iloc[0]
fbc
officer 0
ii 0
police 0
i 0
assistant 0
..
security 0
geologist 0
utilities 0
gardener 0
principle 0
Name: fire battalion chief, Length: 327, dtype: int64
We can stack these two vectors horizontally.
pair_counts = (
pd.concat([dfc, fbc], axis=1)
.sort_values(by=['deputy fire chief', 'fire battalion chief'], ascending=False)
.head(10)
.T
)
pair_counts
| fire | chief | deputy | battalion | officer | ii | police | i | assistant | engineer | |
|---|---|---|---|---|---|---|---|---|---|---|
| deputy fire chief | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| fire battalion chief | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
One way to measure how similar the above two vectors are is through their dot product.
np.sum(pair_counts.iloc[0] * pair_counts.iloc[1])
2
Here, since both vectors consist only of 1s and 0s, the dot product is equal to the number of shared words between the two job titles.
 (source)
(source)To find the job title that is most similar to 'deputy fire chief', we can compute the dot product of the 'deputy fire chief' word vector with all other titles' word vectors, and find the title with the highest dot product.
counts_df.head()
| officer | ii | police | i | assistant | fire | engineer | civil | iii | technician | ... | estate | stores | assets | treasurer | risk | security | geologist | utilities | gardener | principle | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Job Title | |||||||||||||||||||||
| city attorney | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| mayor | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| investment officer | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| police officer | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| independent budget analyst | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
5 rows × 327 columns
dfc
officer 0
ii 0
police 0
i 0
assistant 0
..
security 0
geologist 0
utilities 0
gardener 0
principle 0
Name: deputy fire chief, Length: 327, dtype: int64
To do so, we can apply np.dot to each row that doesn't correspond to 'deputy fire chief'.
dots = (
counts_df[counts_df.index != 'deputy fire chief']
.apply(lambda s: np.dot(s, dfc), axis=1)
.sort_values(ascending=False)
)
dots
Job Title
fire battalion chief 2
fire battalion chief 2
assistant fire chief 2
fire battalion chief 2
fire battalion chief 2
..
finance analyst iii 0
associate engineer traffic 0
supervising procurement contracting officer 0
sanitation driver ii 0
city attorney 0
Length: 12292, dtype: int64
The unique job titles that are most similar to 'deputy fire chief' are given below.
np.unique(dots.index[dots == dots.max()])
array(['assistant deputy chief operating officer', 'assistant fire chief',
'deputy chief operating officer', 'fire battalion chief',
'fire chief'], dtype=object)
Note that they all share two words in common with 'deputy fire chief'.
Note: To truly use the dot product as a measure of similarity, we should normalize by the lengths of the word vectors.
To measure the similarity between two word vectors, we compute their normalized dot product, also known as their cosine similarity.
$$\cos \theta = \boxed{\frac{\vec{a} \cdot \vec{b}}{|\vec{a}| | \vec{b}|}}$$If $\cos \theta$ is large, the two word vectors are similar. It is important to normalize by the lengths of the vectors, otherwise texts with more words will have artificially high similarities with other texts.
Note: Sometimes, you will see the cosine distance being used. It is the complement of cosine similarity:
$$\text{dist}(\vec{a}, \vec{b}) = 1 - \cos \theta$$
If $\text{dist}(\vec{a}, \vec{b})$ is small, the two word vectors are similar.
Given a set of documents, to find the most similar text to one document $d$ in particular:
doc and column word is the number of occurrences of word in doc.Consider the following three documents.
sentences = pd.Series([
'I really really want global peace',
'I must enjoy global warming',
'We must solve climate change'
])
sentences
0 I really really want global peace 1 I must enjoy global warming 2 We must solve climate change dtype: object
Let's represent each document using the bag of words model.
unique_words = pd.Series(sentences.str.split().sum()).value_counts()
unique_words
I 2 really 2 global 2 must 2 want 1 peace 1 enjoy 1 warming 1 We 1 solve 1 climate 1 change 1 dtype: int64
counts_dict = {}
for word in unique_words.index:
re_pat = fr'\b{word}\b'
counts_dict[word] = sentences.str.count(re_pat).astype(int).tolist()
counts_df = pd.DataFrame(counts_dict).set_index(sentences)
counts_df
| I | really | global | must | want | peace | enjoy | warming | We | solve | climate | change | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I really really want global peace | 1 | 2 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| I must enjoy global warming | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| We must solve climate change | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
Let's now find the cosine similarity between each document.
counts_df
| I | really | global | must | want | peace | enjoy | warming | We | solve | climate | change | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I really really want global peace | 1 | 2 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| I must enjoy global warming | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| We must solve climate change | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
def sim_pair(s1, s2):
return np.dot(s1, s2) / (np.linalg.norm(s1) * np.linalg.norm(s2))
# Look at the documentation of the .corr method to see how this works!
counts_df.T.corr(sim_pair)
| I really really want global peace | I must enjoy global warming | We must solve climate change | |
|---|---|---|---|
| I really really want global peace | 1.000000 | 0.316228 | 0.0 |
| I must enjoy global warming | 0.316228 | 1.000000 | 0.2 |
| We must solve climate change | 0.000000 | 0.200000 | 1.0 |
Issue: Bag of words only encodes the words that each document uses, not their meanings.
Remember, the key assumption underlying the bag of words model is that two documents are similar if they share many words in common.
'deputy fire chief' and 'chief fire deputy' are treated as the same.'I love data science' and 'I hate data science' share 75% of their words, but have very different meanings.'deputy' and 'fire' have the same importance, even though 'fire' is probably more important in describing someone's job title.Issue: The bag of words model doesn't know which words are "important" in a document. Consider the following document:
How do we determine which words are important?
Goal: Find a way of quantifying the importance of a word in a document by balancing the above two factors, i.e. find the word that best summarizes a document.
Goal: Quantify how well word $t$ summarizes document $d$.
The term frequency-inverse document frequency (TF-IDF) of word $t$ in document $d$ is the product:
$$ \begin{align*}\text{tfidf}(t, d) &= \text{tf}(t, d) \cdot \text{idf}(t) \\\ &= \frac{\text{# of occurrences of $t$ in $d$}}{\text{total # of words in $d$}} \cdot \log \left(\frac{\text{total # of documents}}{\text{# of documents in which $t$ appears}} \right) \end{align*} $$Question: What is the TF-IDF of "global" in the second sentence?
sentences
0 I really really want global peace 1 I must enjoy global warming 2 We must solve climate change dtype: object
Answer
tf = sentences.iloc[1].count('global') / len(sentences.iloc[1].split())
tf
0.2
idf = np.log(len(sentences) / sentences.str.contains('global').sum())
idf
0.4054651081081644
tf * idf
0.08109302162163289
Question: Is this big or small? Is "global" the best summary of the second sentence?
On its own, the TF-IDF of a word in a document doesn't really tell us anything; we must compare it to TF-IDFs of other words in that same document.
sentences
0 I really really want global peace 1 I must enjoy global warming 2 We must solve climate change dtype: object
unique_words = np.unique(sentences.str.split().sum())
unique_words
array(['I', 'We', 'change', 'climate', 'enjoy', 'global', 'must', 'peace',
'really', 'solve', 'want', 'warming'], dtype='<U7')
tfidf_dict = {}
for word in unique_words:
re_pat = fr'\b{word}\b'
tf = sentences.str.count(re_pat) / sentences.str.split().str.len()
idf = np.log(len(sentences) / sentences.str.contains(re_pat).sum())
tfidf_dict[word] = tf * idf
tfidf = pd.DataFrame(tfidf_dict).set_index(sentences)
tfidf
| I | We | change | climate | enjoy | global | must | peace | really | solve | want | warming | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I really really want global peace | 0.067578 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.067578 | 0.000000 | 0.183102 | 0.366204 | 0.000000 | 0.183102 | 0.000000 |
| I must enjoy global warming | 0.081093 | 0.000000 | 0.000000 | 0.000000 | 0.219722 | 0.081093 | 0.081093 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.219722 |
| We must solve climate change | 0.000000 | 0.219722 | 0.219722 | 0.219722 | 0.000000 | 0.000000 | 0.081093 | 0.000000 | 0.000000 | 0.219722 | 0.000000 | 0.000000 |
tfidf
| I | We | change | climate | enjoy | global | must | peace | really | solve | want | warming | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I really really want global peace | 0.067578 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.067578 | 0.000000 | 0.183102 | 0.366204 | 0.000000 | 0.183102 | 0.000000 |
| I must enjoy global warming | 0.081093 | 0.000000 | 0.000000 | 0.000000 | 0.219722 | 0.081093 | 0.081093 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.219722 |
| We must solve climate change | 0.000000 | 0.219722 | 0.219722 | 0.219722 | 0.000000 | 0.000000 | 0.081093 | 0.000000 | 0.000000 | 0.219722 | 0.000000 | 0.000000 |
The above DataFrame tells us that:
'peace' in the first sentence is 0.183102,'climate' in the second sentence is 0.Note that there are two ways that $\text{tfidf}(t, d) = \text{tf}(t, d) \cdot \text{idf}(t)$ can be 0:
The word that best summarizes a document is the word with the highest TF-IDF for that document:
tfidf
| I | We | change | climate | enjoy | global | must | peace | really | solve | want | warming | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I really really want global peace | 0.067578 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.067578 | 0.000000 | 0.183102 | 0.366204 | 0.000000 | 0.183102 | 0.000000 |
| I must enjoy global warming | 0.081093 | 0.000000 | 0.000000 | 0.000000 | 0.219722 | 0.081093 | 0.081093 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.219722 |
| We must solve climate change | 0.000000 | 0.219722 | 0.219722 | 0.219722 | 0.000000 | 0.000000 | 0.081093 | 0.000000 | 0.000000 | 0.219722 | 0.000000 | 0.000000 |
tfidf.idxmax(axis=1)
I really really want global peace really I must enjoy global warming enjoy We must solve climate change We dtype: object
Look closely at the rows of tfidf – in documents 1 and 2, the max TF-IDF is not unique!
The 2023 State of the Union address was on February 7th, 2023.
YouTubeVideo('gzcBTUvVp7M')
sotu = open('data/stateoftheunion1790-2023.txt').read()
len(sotu)
10577941
The entire corpus (another word for "set of documents") is over 10 million characters long... let's not display it in our notebook.
print(sotu[:16000])
The Project Gutenberg EBook of Complete State of the Union Addresses, from 1790 to the Present. Speeches beginning in 2002 are from UCSB The American Presidency Project. Speeches from 2018-2023 were manually downloaded from whitehouse.gov. Character set encoding: UTF8 The addresses are separated by three asterisks CONTENTS George Washington, State of the Union Address, January 8, 1790 George Washington, State of the Union Address, December 8, 1790 George Washington, State of the Union Address, October 25, 1791 George Washington, State of the Union Address, November 6, 1792 George Washington, State of the Union Address, December 3, 1793 George Washington, State of the Union Address, November 19, 1794 George Washington, State of the Union Address, December 8, 1795 George Washington, State of the Union Address, December 7, 1796 John Adams, State of the Union Address, November 22, 1797 John Adams, State of the Union Address, December 8, 1798 John Adams, State of the Union Address, December 3, 1799 John Adams, State of the Union Address, November 11, 1800 Thomas Jefferson, State of the Union Address, December 8, 1801 Thomas Jefferson, State of the Union Address, December 15, 1802 Thomas Jefferson, State of the Union Address, October 17, 1803 Thomas Jefferson, State of the Union Address, November 8, 1804 Thomas Jefferson, State of the Union Address, December 3, 1805 Thomas Jefferson, State of the Union Address, December 2, 1806 Thomas Jefferson, State of the Union Address, October 27, 1807 Thomas Jefferson, State of the Union Address, November 8, 1808 James Madison, State of the Union Address, November 29, 1809 James Madison, State of the Union Address, December 5, 1810 James Madison, State of the Union Address, November 5, 1811 James Madison, State of the Union Address, November 4, 1812 James Madison, State of the Union Address, December 7, 1813 James Madison, State of the Union Address, September 20, 1814 James Madison, State of the Union Address, December 5, 1815 James Madison, State of the Union Address, December 3, 1816 James Monroe, State of the Union Address, December 12, 1817 James Monroe, State of the Union Address, November 16, 1818 James Monroe, State of the Union Address, December 7, 1819 James Monroe, State of the Union Address, November 14, 1820 James Monroe, State of the Union Address, December 3, 1821 James Monroe, State of the Union Address, December 3, 1822 James Monroe, State of the Union Address, December 2, 1823 James Monroe, State of the Union Address, December 7, 1824 John Quincy Adams, State of the Union Address, December 6, 1825 John Quincy Adams, State of the Union Address, December 5, 1826 John Quincy Adams, State of the Union Address, December 4, 1827 John Quincy Adams, State of the Union Address, December 2, 1828 Andrew Jackson, State of the Union Address, December 8, 1829 Andrew Jackson, State of the Union Address, December 6, 1830 Andrew Jackson, State of the Union Address, December 6, 1831 Andrew Jackson, State of the Union Address, December 4, 1832 Andrew Jackson, State of the Union Address, December 3, 1833 Andrew Jackson, State of the Union Address, December 1, 1834 Andrew Jackson, State of the Union Address, December 7, 1835 Andrew Jackson, State of the Union Address, December 5, 1836 Martin van Buren, State of the Union Address, December 5, 1837 Martin van Buren, State of the Union Address, December 3, 1838 Martin van Buren, State of the Union Address, December 2, 1839 Martin van Buren, State of the Union Address, December 5, 1840 John Tyler, State of the Union Address, December 7, 1841 John Tyler, State of the Union Address, December 6, 1842 John Tyler, State of the Union Address, December 6, 1843 John Tyler, State of the Union Address, December 3, 1844 James Polk, State of the Union Address, December 2, 1845 James Polk, State of the Union Address, December 8, 1846 James Polk, State of the Union Address, December 7, 1847 James Polk, State of the Union Address, December 5, 1848 Zachary Taylor, State of the Union Address, December 4, 1849 Millard Fillmore, State of the Union Address, December 2, 1850 Millard Fillmore, State of the Union Address, December 2, 1851 Millard Fillmore, State of the Union Address, December 6, 1852 Franklin Pierce, State of the Union Address, December 5, 1853 Franklin Pierce, State of the Union Address, December 4, 1854 Franklin Pierce, State of the Union Address, December 31, 1855 Franklin Pierce, State of the Union Address, December 2, 1856 James Buchanan, State of the Union Address, December 8, 1857 James Buchanan, State of the Union Address, December 6, 1858 James Buchanan, State of the Union Address, December 19, 1859 James Buchanan, State of the Union Address, December 3, 1860 Abraham Lincoln, State of the Union Address, December 3, 1861 Abraham Lincoln, State of the Union Address, December 1, 1862 Abraham Lincoln, State of the Union Address, December 8, 1863 Abraham Lincoln, State of the Union Address, December 6, 1864 Andrew Johnson, State of the Union Address, December 4, 1865 Andrew Johnson, State of the Union Address, December 3, 1866 Andrew Johnson, State of the Union Address, December 3, 1867 Andrew Johnson, State of the Union Address, December 9, 1868 Ulysses S. Grant, State of the Union Address, December 6, 1869 Ulysses S. Grant, State of the Union Address, December 5, 1870 Ulysses S. Grant, State of the Union Address, December 4, 1871 Ulysses S. Grant, State of the Union Address, December 2, 1872 Ulysses S. Grant, State of the Union Address, December 1, 1873 Ulysses S. Grant, State of the Union Address, December 7, 1874 Ulysses S. Grant, State of the Union Address, December 7, 1875 Ulysses S. Grant, State of the Union Address, December 5, 1876 Rutherford B. Hayes, State of the Union Address, December 3, 1877 Rutherford B. Hayes, State of the Union Address, December 2, 1878 Rutherford B. Hayes, State of the Union Address, December 1, 1879 Rutherford B. Hayes, State of the Union Address, December 6, 1880 Chester A. Arthur, State of the Union Address, December 6, 1881 Chester A. Arthur, State of the Union Address, December 4, 1882 Chester A. Arthur, State of the Union Address, December 4, 1883 Chester A. Arthur, State of the Union Address, December 1, 1884 Grover Cleveland, State of the Union Address, December 8, 1885 Grover Cleveland, State of the Union Address, December 6, 1886 Grover Cleveland, State of the Union Address, December 6, 1887 Grover Cleveland, State of the Union Address, December 3, 1888 Benjamin Harrison, State of the Union Address, December 3, 1889 Benjamin Harrison, State of the Union Address, December 1, 1890 Benjamin Harrison, State of the Union Address, December 9, 1891 Benjamin Harrison, State of the Union Address, December 6, 1892 William McKinley, State of the Union Address, December 6, 1897 William McKinley, State of the Union Address, December 5, 1898 William McKinley, State of the Union Address, December 5, 1899 William McKinley, State of the Union Address, December 3, 1900 Theodore Roosevelt, State of the Union Address, December 3, 1901 Theodore Roosevelt, State of the Union Address, December 2, 1902 Theodore Roosevelt, State of the Union Address, December 7, 1903 Theodore Roosevelt, State of the Union Address, December 6, 1904 Theodore Roosevelt, State of the Union Address, December 5, 1905 Theodore Roosevelt, State of the Union Address, December 3, 1906 Theodore Roosevelt, State of the Union Address, December 3, 1907 Theodore Roosevelt, State of the Union Address, December 8, 1908 William H. Taft, State of the Union Address, December 7, 1909 William H. Taft, State of the Union Address, December 6, 1910 William H. Taft, State of the Union Address, December 5, 1911 William H. Taft, State of the Union Address, December 3, 1912 Woodrow Wilson, State of the Union Address, December 2, 1913 Woodrow Wilson, State of the Union Address, December 8, 1914 Woodrow Wilson, State of the Union Address, December 7, 1915 Woodrow Wilson, State of the Union Address, December 5, 1916 Woodrow Wilson, State of the Union Address, December 4, 1917 Woodrow Wilson, State of the Union Address, December 2, 1918 Woodrow Wilson, State of the Union Address, December 2, 1919 Woodrow Wilson, State of the Union Address, December 7, 1920 Warren Harding, State of the Union Address, December 6, 1921 Warren Harding, State of the Union Address, December 8, 1922 Calvin Coolidge, State of the Union Address, December 6, 1923 Calvin Coolidge, State of the Union Address, December 3, 1924 Calvin Coolidge, State of the Union Address, December 8, 1925 Calvin Coolidge, State of the Union Address, December 7, 1926 Calvin Coolidge, State of the Union Address, December 6, 1927 Calvin Coolidge, State of the Union Address, December 4, 1928 Herbert Hoover, State of the Union Address, December 3, 1929 Herbert Hoover, State of the Union Address, December 2, 1930 Herbert Hoover, State of the Union Address, December 8, 1931 Herbert Hoover, State of the Union Address, December 6, 1932 Franklin D. Roosevelt, State of the Union Address, January 3, 1934 Franklin D. Roosevelt, State of the Union Address, January 4, 1935 Franklin D. Roosevelt, State of the Union Address, January 3, 1936 Franklin D. Roosevelt, State of the Union Address, January 6, 1937 Franklin D. Roosevelt, State of the Union Address, January 3, 1938 Franklin D. Roosevelt, State of the Union Address, January 4, 1939 Franklin D. Roosevelt, State of the Union Address, January 3, 1940 Franklin D. Roosevelt, State of the Union Address, January 6, 1941 Franklin D. Roosevelt, State of the Union Address, January 6, 1942 Franklin D. Roosevelt, State of the Union Address, January 7, 1943 Franklin D. Roosevelt, State of the Union Address, January 11, 1944 Franklin D. Roosevelt, State of the Union Address, January 6, 1945 Harry S. Truman, State of the Union Address, January 21, 1946 Harry S. Truman, State of the Union Address, January 6, 1947 Harry S. Truman, State of the Union Address, January 7, 1948 Harry S. Truman, State of the Union Address, January 5, 1949 Harry S. Truman, State of the Union Address, January 4, 1950 Harry S. Truman, State of the Union Address, January 8, 1951 Harry S. Truman, State of the Union Address, January 9, 1952 Harry S. Truman, State of the Union Address, January 7, 1953 Dwight D. Eisenhower, State of the Union Address, February 2, 1953 Dwight D. Eisenhower, State of the Union Address, January 7, 1954 Dwight D. Eisenhower, State of the Union Address, January 6, 1955 Dwight D. Eisenhower, State of the Union Address, January 5, 1956 Dwight D. Eisenhower, State of the Union Address, January 10, 1957 Dwight D. Eisenhower, State of the Union Address, January 9, 1958 Dwight D. Eisenhower, State of the Union Address, January 9, 1959 Dwight D. Eisenhower, State of the Union Address, January 7, 1960 Dwight D. Eisenhower, State of the Union Address, January 12, 1961 John F. Kennedy, State of the Union Address, January 30, 1961 John F. Kennedy, State of the Union Address, January 11, 1962 John F. Kennedy, State of the Union Address, January 14, 1963 Lyndon B. Johnson, State of the Union Address, January 8, 1964 Lyndon B. Johnson, State of the Union Address, January 4, 1965 Lyndon B. Johnson, State of the Union Address, January 12, 1966 Lyndon B. Johnson, State of the Union Address, January 10, 1967 Lyndon B. Johnson, State of the Union Address, January 17, 1968 Lyndon B. Johnson, State of the Union Address, January 14, 1969 Richard Nixon, State of the Union Address, January 22, 1970 Richard Nixon, State of the Union Address, January 22, 1971 Richard Nixon, State of the Union Address, January 20, 1972 Richard Nixon, State of the Union Address, February 2, 1973 Richard Nixon, State of the Union Address, January 30, 1974 Gerald R. Ford, State of the Union Address, January 15, 1975 Gerald R. Ford, State of the Union Address, January 19, 1976 Gerald R. Ford, State of the Union Address, January 12, 1977 Jimmy Carter, State of the Union Address, January 19, 1978 Jimmy Carter, State of the Union Address, January 25, 1979 Jimmy Carter, State of the Union Address, January 21, 1980 Jimmy Carter, State of the Union Address, January 16, 1981 Ronald Reagan, State of the Union Address, January 26, 1982 Ronald Reagan, State of the Union Address, January 25, 1983 Ronald Reagan, State of the Union Address, January 25, 1984 Ronald Reagan, State of the Union Address, February 6, 1985 Ronald Reagan, State of the Union Address, February 4, 1986 Ronald Reagan, State of the Union Address, January 27, 1987 Ronald Reagan, State of the Union Address, January 25, 1988 George H.W. Bush, Address on Administration Goals, February 9, 1989 George H.W. Bush, State of the Union Address, January 31, 1990 George H.W. Bush, State of the Union Address, January 29, 1991 George H.W. Bush, State of the Union Address, January 28, 1992 William J. Clinton, Address on Administration Goals, February 17, 1993 William J. Clinton, State of the Union Address, January 25, 1994 William J. Clinton, State of the Union Address, January 24, 1995 William J. Clinton, State of the Union Address, January 23, 1996 William J. Clinton, State of the Union Address, February 4, 1997 William J. Clinton, State of the Union Address, January 27, 1998 William J. Clinton, State of the Union Address, January 19, 1999 William J. Clinton, State of the Union Address, January 27, 2000 George W. Bush, Address on Administration Goals (Budget Message), February 27, 2001 George W. Bush, State of the Union Address, September 20, 2001 George W. Bush, State of the Union Address, January 29, 2002 George W. Bush, State of the Union Address, January 28, 2003 George W. Bush, State of the Union Address, January 20, 2004 George W. Bush, State of the Union Address, February 2, 2005 George W. Bush, State of the Union Address, January 31, 2006 George W. Bush, State of the Union Address, January 23, 2007 George W. Bush, State of the Union Address, January 31, 2008 Barack Obama, Address Before a Joint Session of Congress, February 24, 2009 Barack Obama, State of the Union Address, January 27, 2010 Barack Obama, State of the Union Address, January 25, 2011 Barack Obama, State of the Union Address, January 24, 2012 Barack Obama, State of the Union Address, February 12, 2013 Barack Obama, State of the Union Address, January 28, 2014 Barack Obama, State of the Union Address, January 20, 2015 Barack Obama, State of the Union Address, January 12, 2016 Donald J. Trump, Address Before a Joint Session of Congress, February 27, 2017 Donald J. Trump, Address Before a Joint Session of Congress, January 30, 2018 Donald J. Trump, Address Before a Joint Session of Congress, February 5, 2019 Donald J. Trump, Address Before a Joint Session of Congress, February 4, 2020 Joseph R. Biden Jr., Address Before a Joint Session of Congress, April 28, 2021 Joseph R. Biden Jr., Address Before a Joint Session of Congress, March 1, 2022 *** State of the Union Address George Washington January 8, 1790 Fellow-Citizens of the Senate and House of Representatives: I embrace with great satisfaction the opportunity which now presents itself of congratulating you on the present favorable prospects of our public affairs. The recent accession of the important state of North Carolina to the Constitution of the United States (of which official information has been received), the rising credit and respectability of our country, the general and increasing good will toward the government of the Union, and the concord, peace, and plenty with which we are
Each speech is separated by '***'.
speeches = sotu.split('\n***\n')[1:]
len(speeches)
233
Note that each "speech" currently contains other information, like the name of the president and the date of the address.
print(speeches[-1][:1000])
State of the Union Address Joseph R. Biden Jr. February 7, 2023 Mr. Speaker. Madam Vice President. Our First Lady and Second Gentleman. Members of Congress and the Cabinet. Leaders of our military. Mr. Chief Justice, Associate Justices, and retired Justices of the Supreme Court. And you, my fellow Americans. I start tonight by congratulating the members of the 118th Congress and the new Speaker of the House, Kevin McCarthy. Mr. Speaker, I look forward to working together. I also want to congratulate the new leader of the House Democrats and the first Black House Minority Leader in history, Hakeem Jeffries. Congratulations to the longest serving Senate leader in history, Mitch McConnell. And congratulations to Chuck Schumer for another term as Senate Majority Leader, this time with an even bigger majority. And I want to give special recognition to someone who I think will be considered the greatest Speaker in the history of this country, Nancy Pelosi. The story of Amer
Let's extract just the speech text.
def extract_struct(speech):
L = speech.strip().split('\n', maxsplit=3)
L[3] = re.sub(r"[^A-Za-z' ]", ' ', L[3]).lower()
return dict(zip(['speech', 'president', 'date', 'contents'], L))
speeches_df = pd.DataFrame(list(map(extract_struct, speeches)))
speeches_df
| speech | president | date | contents | |
|---|---|---|---|---|
| 0 | State of the Union Address | George Washington | January 8, 1790 | fellow citizens of the senate and house of re... |
| 1 | State of the Union Address | George Washington | December 8, 1790 | fellow citizens of the senate and house of re... |
| 2 | State of the Union Address | George Washington | October 25, 1791 | fellow citizens of the senate and house of re... |
| 3 | State of the Union Address | George Washington | November 6, 1792 | fellow citizens of the senate and house of re... |
| 4 | State of the Union Address | George Washington | December 3, 1793 | fellow citizens of the senate and house of re... |
| ... | ... | ... | ... | ... |
| 228 | State of the Union Address | Donald J. Trump | February 5, 2019 | madam speaker mr vice president members of... |
| 229 | State of the Union Address | Donald J. Trump | February 4, 2020 | thank you very much thank you thank you ver... |
| 230 | State of the Union Address | Joseph R. Biden Jr. | April 28, 2021 | thank you thank you thank you good to be b... |
| 231 | State of the Union Address | Joseph R. Biden Jr. | March 1, 2022 | madam speaker madam vice president and our ... |
| 232 | State of the Union Address | Joseph R. Biden Jr. | February 7, 2023 | mr speaker madam vice president our firs... |
233 rows × 4 columns
Here, a "document" is a speech. We have 233 documents.
speeches_df.head()
| speech | president | date | contents | |
|---|---|---|---|---|
| 0 | State of the Union Address | George Washington | January 8, 1790 | fellow citizens of the senate and house of re... |
| 1 | State of the Union Address | George Washington | December 8, 1790 | fellow citizens of the senate and house of re... |
| 2 | State of the Union Address | George Washington | October 25, 1791 | fellow citizens of the senate and house of re... |
| 3 | State of the Union Address | George Washington | November 6, 1792 | fellow citizens of the senate and house of re... |
| 4 | State of the Union Address | George Washington | December 3, 1793 | fellow citizens of the senate and house of re... |
A rough sketch of what we'll compute:
for each word t:
for each speech d:
compute tfidf(t, d)unique_words = pd.Series(speeches_df['contents'].str.split().sum()).value_counts()
unique_words
the 147042
of 94373
to 60611
and 60540
in 38190
...
jacket 1
strait 1
isle 1
poignantly 1
chanted 1
Length: 24188, dtype: int64
unique_words = unique_words.iloc[:500].index
tfidf_dict = {}
tf_denom = speeches_df['contents'].str.split().str.len()
for word in unique_words:
re_pat = fr' {word} ' # Imperfect pattern for speed.
tf = speeches_df['contents'].str.count(re_pat) / tf_denom
idf = np.log(len(speeches_df) / speeches_df['contents'].str.contains(re_pat).sum())
tfidf_dict[word] = tf * idf
tfidf = pd.DataFrame(tfidf_dict)
tfidf.head()
| the | of | to | and | in | a | that | for | be | our | ... | desire | call | submitted | increasing | months | point | trust | throughout | set | object | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.000000 | 0.000328 | 0.000000 | 0.00038 | 0.0 | 0.0 | 0.000429 | 0.000000 | 0.000000 | 0.002043 |
| 1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.000000 | 0.000255 | 0.000438 | 0.00000 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.000000 | 0.001057 |
| 2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.000000 | 0.000000 | 0.000267 | 0.00018 | 0.0 | 0.0 | 0.000406 | 0.000000 | 0.000348 | 0.000644 |
| 3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.000286 | 0.000171 | 0.000000 | 0.00000 | 0.0 | 0.0 | 0.000670 | 0.000217 | 0.000000 | 0.000709 |
| 4 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.000610 | 0.000000 | 0.000000 | 0.00000 | 0.0 | 0.0 | 0.000238 | 0.000462 | 0.000000 | 0.000377 |
5 rows × 500 columns
Note that the TF-IDFs of many common words are all 0!
By using idxmax, we can find the word with the highest TF-IDF in each speech.
summaries = tfidf.idxmax(axis=1)
summaries
0 object
1 convention
2 provision
3 provision
4 ought
...
228 tonight
229 tonight
230 it's
231 tonight
232 it's
Length: 233, dtype: object
What if we want to see the 5 words with the highest TF-IDFs, for each speech?
def five_largest(row):
return list(row.index[row.argsort()][-5:])
keywords = tfidf.apply(five_largest, axis=1)
keywords_df = pd.concat([
speeches_df['president'],
speeches_df['date'],
keywords
], axis=1)
Run the cell below to see every single row of keywords_df.
with pd.option_context('display.max_rows', 300):
display(keywords_df)
| president | date | 0 | |
|---|---|---|---|
| 0 | George Washington | January 8, 1790 | [your, proper, regard, ought, object] |
| 1 | George Washington | December 8, 1790 | [case, established, object, commerce, convention] |
| 2 | George Washington | October 25, 1791 | [community, upon, lands, proper, provision] |
| 3 | George Washington | November 6, 1792 | [subject, upon, information, proper, provision] |
| 4 | George Washington | December 3, 1793 | [having, vessels, executive, shall, ought] |
| 5 | George Washington | November 19, 1794 | [too, army, let, ought, constitution] |
| 6 | George Washington | December 8, 1795 | [army, prevent, object, provision, treaty] |
| 7 | George Washington | December 7, 1796 | [republic, treaty, britain, ought, object] |
| 8 | John Adams | November 22, 1797 | [spain, british, claims, treaty, vessels] |
| 9 | John Adams | December 8, 1798 | [st, minister, treaty, spain, commerce] |
| 10 | John Adams | December 3, 1799 | [civil, period, british, minister, treaty] |
| 11 | John Adams | November 11, 1800 | [experience, protection, navy, commerce, ought] |
| 12 | Thomas Jefferson | December 8, 1801 | [consideration, shall, object, vessels, subject] |
| 13 | Thomas Jefferson | December 15, 1802 | [shall, debt, naval, duties, vessels] |
| 14 | Thomas Jefferson | October 17, 1803 | [debt, vessels, sum, millions, friendly] |
| 15 | Thomas Jefferson | November 8, 1804 | [received, convention, having, due, friendly] |
| 16 | Thomas Jefferson | December 3, 1805 | [families, convention, sum, millions, vessels] |
| 17 | Thomas Jefferson | December 2, 1806 | [due, consideration, millions, shall, spain] |
| 18 | Thomas Jefferson | October 27, 1807 | [whether, army, british, vessels, shall] |
| 19 | Thomas Jefferson | November 8, 1808 | [thus, british, millions, commerce, her] |
| 20 | James Madison | November 29, 1809 | [cases, having, due, british, minister] |
| 21 | James Madison | December 5, 1810 | [provisions, view, minister, commerce, british] |
| 22 | James Madison | November 5, 1811 | [britain, provisions, commerce, minister, brit... |
| 23 | James Madison | November 4, 1812 | [nor, subject, provisions, britain, british] |
| 24 | James Madison | December 7, 1813 | [number, having, naval, britain, british] |
| 25 | James Madison | September 20, 1814 | [naval, vessels, britain, his, british] |
| 26 | James Madison | December 5, 1815 | [debt, treasury, millions, establishment, sum] |
| 27 | James Madison | December 3, 1816 | [constitution, annual, sum, treasury, british] |
| 28 | James Monroe | December 12, 1817 | [improvement, territory, indian, millions, lands] |
| 29 | James Monroe | November 16, 1818 | [minister, object, territory, her, spain] |
| 30 | James Monroe | December 7, 1819 | [parties, friendly, minister, treaty, spain] |
| 31 | James Monroe | November 14, 1820 | [amount, minister, extent, vessels, spain] |
| 32 | James Monroe | December 3, 1821 | [powers, duties, revenue, spain, vessels] |
| 33 | James Monroe | December 3, 1822 | [object, proper, vessels, spain, convention] |
| 34 | James Monroe | December 2, 1823 | [th, department, object, minister, spain] |
| 35 | James Monroe | December 7, 1824 | [spain, governments, convention, parties, object] |
| 36 | John Quincy Adams | December 6, 1825 | [officers, commerce, condition, upon, improvem... |
| 37 | John Quincy Adams | December 5, 1826 | [commercial, upon, vessels, british, duties] |
| 38 | John Quincy Adams | December 4, 1827 | [lands, british, receipts, upon, th] |
| 39 | John Quincy Adams | December 2, 1828 | [duties, revenue, upon, commercial, britain] |
| 40 | Andrew Jackson | December 8, 1829 | [attention, subject, her, upon, duties] |
| 41 | Andrew Jackson | December 6, 1830 | [general, subject, character, vessels, upon] |
| 42 | Andrew Jackson | December 6, 1831 | [indian, commerce, claims, treaty, minister] |
| 43 | Andrew Jackson | December 4, 1832 | [general, subject, duties, lands, commerce] |
| 44 | Andrew Jackson | December 3, 1833 | [treasury, convention, minister, spain, duties] |
| 45 | Andrew Jackson | December 1, 1834 | [bill, treaty, minister, claims, upon] |
| 46 | Andrew Jackson | December 7, 1835 | [treaty, upon, claims, subject, minister] |
| 47 | Andrew Jackson | December 5, 1836 | [upon, treasury, duties, revenue, banks] |
| 48 | Martin van Buren | December 5, 1837 | [price, subject, upon, banks, lands] |
| 49 | Martin van Buren | December 3, 1838 | [subject, upon, indian, banks, court] |
| 50 | Martin van Buren | December 2, 1839 | [duties, treasury, extent, institutions, banks] |
| 51 | Martin van Buren | December 5, 1840 | [general, revenue, upon, extent, having] |
| 52 | John Tyler | December 7, 1841 | [banks, britain, amount, duties, treasury] |
| 53 | John Tyler | December 6, 1842 | [claims, minister, thus, amount, treasury] |
| 54 | John Tyler | December 6, 1843 | [treasury, british, her, minister, mexico] |
| 55 | John Tyler | December 3, 1844 | [minister, upon, treaty, her, mexico] |
| 56 | James Polk | December 2, 1845 | [british, convention, territory, duties, mexico] |
| 57 | James Polk | December 8, 1846 | [army, territory, minister, her, mexico] |
| 58 | James Polk | December 7, 1847 | [amount, treaty, her, army, mexico] |
| 59 | James Polk | December 5, 1848 | [tariff, upon, bill, constitution, mexico] |
| 60 | Zachary Taylor | December 4, 1849 | [territory, treaty, recommend, minister, mexico] |
| 61 | Millard Fillmore | December 2, 1850 | [recommend, claims, upon, mexico, duties] |
| 62 | Millard Fillmore | December 2, 1851 | [department, annual, fiscal, subject, mexico] |
| 63 | Millard Fillmore | December 6, 1852 | [duties, navy, mexico, subject, her] |
| 64 | Franklin Pierce | December 5, 1853 | [commercial, regard, upon, construction, subject] |
| 65 | Franklin Pierce | December 4, 1854 | [character, duties, naval, minister, property] |
| 66 | Franklin Pierce | December 31, 1855 | [constitution, british, territory, convention,... |
| 67 | Franklin Pierce | December 2, 1856 | [institutions, property, condition, thus, terr... |
| 68 | James Buchanan | December 8, 1857 | [treaty, constitution, territory, convention, ... |
| 69 | James Buchanan | December 6, 1858 | [june, mexico, minister, constitution, territory] |
| 70 | James Buchanan | December 19, 1859 | [minister, th, fiscal, mexico, june] |
| 71 | James Buchanan | December 3, 1860 | [minister, duties, claims, convention, constit... |
| 72 | Abraham Lincoln | December 3, 1861 | [army, claims, labor, capital, court] |
| 73 | Abraham Lincoln | December 1, 1862 | [upon, population, shall, per, sum] |
| 74 | Abraham Lincoln | December 8, 1863 | [upon, receipts, subject, navy, naval] |
| 75 | Abraham Lincoln | December 6, 1864 | [condition, secretary, naval, treasury, navy] |
| 76 | Andrew Johnson | December 4, 1865 | [form, commerce, powers, general, constitution] |
| 77 | Andrew Johnson | December 3, 1866 | [thus, june, constitution, mexico, condition] |
| 78 | Andrew Johnson | December 3, 1867 | [june, value, department, upon, constitution] |
| 79 | Andrew Johnson | December 9, 1868 | [millions, amount, expenditures, june, per] |
| 80 | Ulysses S. Grant | December 6, 1869 | [subject, upon, receipts, per, spain] |
| 81 | Ulysses S. Grant | December 5, 1870 | [her, convention, vessels, spain, british] |
| 82 | Ulysses S. Grant | December 4, 1871 | [object, powers, treaty, desire, recommend] |
| 83 | Ulysses S. Grant | December 2, 1872 | [territory, line, her, britain, treaty] |
| 84 | Ulysses S. Grant | December 1, 1873 | [consideration, banks, subject, amount, claims] |
| 85 | Ulysses S. Grant | December 7, 1874 | [duties, upon, attention, claims, convention] |
| 86 | Ulysses S. Grant | December 7, 1875 | [parties, territory, court, spain, claims] |
| 87 | Ulysses S. Grant | December 5, 1876 | [subject, court, per, commission, claims] |
| 88 | Rutherford B. Hayes | December 3, 1877 | [upon, sum, fiscal, commercial, value] |
| 89 | Rutherford B. Hayes | December 2, 1878 | [per, secretary, fiscal, june, indian] |
| 90 | Rutherford B. Hayes | December 1, 1879 | [subject, territory, june, commission, indian] |
| 91 | Rutherford B. Hayes | December 6, 1880 | [subject, office, relations, attention, commer... |
| 92 | Chester A. Arthur | December 6, 1881 | [spain, international, british, relations, fri... |
| 93 | Chester A. Arthur | December 4, 1882 | [territory, establishment, mexico, internation... |
| 94 | Chester A. Arthur | December 4, 1883 | [total, convention, mexico, commission, treaty] |
| 95 | Chester A. Arthur | December 1, 1884 | [treaty, territory, commercial, secretary, ves... |
| 96 | Grover Cleveland | December 8, 1885 | [duties, vessels, treaty, condition, upon] |
| 97 | Grover Cleveland | December 6, 1886 | [mexico, claims, subject, convention, fiscal] |
| 98 | Grover Cleveland | December 6, 1887 | [condition, sum, thus, price, tariff] |
| 99 | Grover Cleveland | December 3, 1888 | [secretary, treaty, upon, per, june] |
| 100 | Benjamin Harrison | December 3, 1889 | [general, commission, indian, upon, lands] |
| 101 | Benjamin Harrison | December 1, 1890 | [receipts, subject, upon, per, tariff] |
| 102 | Benjamin Harrison | December 9, 1891 | [court, tariff, indian, upon, per] |
| 103 | Benjamin Harrison | December 6, 1892 | [tariff, secretary, upon, value, per] |
| 104 | William McKinley | December 6, 1897 | [conditions, upon, international, territory, s... |
| 105 | William McKinley | December 5, 1898 | [navy, commission, naval, june, spain] |
| 106 | William McKinley | December 5, 1899 | [treaty, officers, commission, international, ... |
| 107 | William McKinley | December 3, 1900 | [settlement, civil, shall, convention, commiss... |
| 108 | Theodore Roosevelt | December 3, 1901 | [army, commercial, conditions, navy, man] |
| 109 | Theodore Roosevelt | December 2, 1902 | [upon, man, navy, conditions, tariff] |
| 110 | Theodore Roosevelt | December 7, 1903 | [june, lands, territory, property, treaty] |
| 111 | Theodore Roosevelt | December 6, 1904 | [cases, conditions, indian, labor, man] |
| 112 | Theodore Roosevelt | December 5, 1905 | [upon, conditions, commission, cannot, man] |
| 113 | Theodore Roosevelt | December 3, 1906 | [upon, navy, tax, court, man] |
| 114 | Theodore Roosevelt | December 3, 1907 | [conditions, navy, upon, army, man] |
| 115 | Theodore Roosevelt | December 8, 1908 | [man, officers, labor, control, banks] |
| 116 | William H. Taft | December 7, 1909 | [convention, banks, court, department, tariff] |
| 117 | William H. Taft | December 6, 1910 | [department, court, commercial, international,... |
| 118 | William H. Taft | December 5, 1911 | [mexico, department, per, tariff, court] |
| 119 | William H. Taft | December 3, 1912 | [tariff, upon, army, per, department] |
| 120 | Woodrow Wilson | December 2, 1913 | [how, shall, upon, mexico, ought] |
| 121 | Woodrow Wilson | December 8, 1914 | [shall, convention, ought, matter, upon] |
| 122 | Woodrow Wilson | December 7, 1915 | [her, navy, millions, economic, cannot] |
| 123 | Woodrow Wilson | December 5, 1916 | [commerce, shall, upon, commission, bill] |
| 124 | Woodrow Wilson | December 4, 1917 | [purpose, her, know, settlement, shall] |
| 125 | Woodrow Wilson | December 2, 1918 | [shall, go, men, upon, back] |
| 126 | Woodrow Wilson | December 2, 1919 | [economic, her, budget, labor, conditions] |
| 127 | Woodrow Wilson | December 7, 1920 | [expenditures, receipts, treasury, budget, upon] |
| 128 | Warren Harding | December 6, 1921 | [capital, ought, problems, conditions, tariff] |
| 129 | Warren Harding | December 8, 1922 | [responsibility, republic, problems, ought, per] |
| 130 | Calvin Coolidge | December 6, 1923 | [conditions, production, commission, ought, co... |
| 131 | Calvin Coolidge | December 3, 1924 | [navy, international, desire, economic, court] |
| 132 | Calvin Coolidge | December 8, 1925 | [international, budget, economic, ought, court] |
| 133 | Calvin Coolidge | December 7, 1926 | [tax, federal, reduction, tariff, ought] |
| 134 | Calvin Coolidge | December 6, 1927 | [construction, banks, per, program, property] |
| 135 | Calvin Coolidge | December 4, 1928 | [federal, department, production, program, per] |
| 136 | Herbert Hoover | December 3, 1929 | [commission, federal, construction, tariff, per] |
| 137 | Herbert Hoover | December 2, 1930 | [about, budget, economic, per, construction] |
| 138 | Herbert Hoover | December 8, 1931 | [upon, construction, federal, economic, banks] |
| 139 | Herbert Hoover | December 6, 1932 | [health, june, value, economic, banks] |
| 140 | Franklin D. Roosevelt | January 3, 1934 | [labor, permanent, problems, cannot, banks] |
| 141 | Franklin D. Roosevelt | January 4, 1935 | [private, work, local, program, cannot] |
| 142 | Franklin D. Roosevelt | January 3, 1936 | [income, shall, let, say, today] |
| 143 | Franklin D. Roosevelt | January 6, 1937 | [powers, convention, needs, help, problems] |
| 144 | Franklin D. Roosevelt | January 3, 1938 | [budget, business, economic, today, income] |
| 145 | Franklin D. Roosevelt | January 4, 1939 | [labor, cannot, capital, income, billion] |
| 146 | Franklin D. Roosevelt | January 3, 1940 | [world, domestic, cannot, economic, today] |
| 147 | Franklin D. Roosevelt | January 6, 1941 | [freedom, problems, cannot, program, today] |
| 148 | Franklin D. Roosevelt | January 6, 1942 | [him, today, know, forces, production] |
| 149 | Franklin D. Roosevelt | January 7, 1943 | [pacific, get, cannot, americans, production] |
| 150 | Franklin D. Roosevelt | January 11, 1944 | [individual, total, know, economic, cannot] |
| 151 | Franklin D. Roosevelt | January 6, 1945 | [cannot, production, army, forces, jobs] |
| 152 | Harry S. Truman | January 21, 1946 | [fiscal, program, billion, million, dollars] |
| 153 | Harry S. Truman | January 6, 1947 | [commission, budget, economic, labor, program] |
| 154 | Harry S. Truman | January 7, 1948 | [tax, billion, today, program, economic] |
| 155 | Harry S. Truman | January 5, 1949 | [economic, price, program, cannot, production] |
| 156 | Harry S. Truman | January 4, 1950 | [income, today, program, programs, economic] |
| 157 | Harry S. Truman | January 8, 1951 | [help, program, production, strength, economic] |
| 158 | Harry S. Truman | January 9, 1952 | [defense, working, program, help, production] |
| 159 | Harry S. Truman | January 7, 1953 | [republic, free, cannot, world, economic] |
| 160 | Dwight D. Eisenhower | February 2, 1953 | [federal, labor, budget, economic, programs] |
| 161 | Dwight D. Eisenhower | January 7, 1954 | [federal, programs, economic, budget, program] |
| 162 | Dwight D. Eisenhower | January 6, 1955 | [problems, federal, economic, programs, program] |
| 163 | Dwight D. Eisenhower | January 5, 1956 | [billion, federal, problems, economic, program] |
| 164 | Dwight D. Eisenhower | January 10, 1957 | [cannot, programs, human, program, economic] |
| 165 | Dwight D. Eisenhower | January 9, 1958 | [program, strength, today, programs, economic] |
| 166 | Dwight D. Eisenhower | January 9, 1959 | [growth, help, billion, programs, economic] |
| 167 | Dwight D. Eisenhower | January 7, 1960 | [freedom, cannot, today, economic, help] |
| 168 | Dwight D. Eisenhower | January 12, 1961 | [million, percent, billion, program, programs] |
| 169 | John F. Kennedy | January 30, 1961 | [budget, programs, problems, economic, program] |
| 170 | John F. Kennedy | January 11, 1962 | [billion, help, program, jobs, cannot] |
| 171 | John F. Kennedy | January 14, 1963 | [help, cannot, tax, percent, billion] |
| 172 | Lyndon B. Johnson | January 8, 1964 | [help, billion, americans, budget, million] |
| 173 | Lyndon B. Johnson | January 4, 1965 | [americans, man, programs, tonight, help] |
| 174 | Lyndon B. Johnson | January 12, 1966 | [program, percent, help, billion, tonight] |
| 175 | Lyndon B. Johnson | January 10, 1967 | [programs, americans, billion, tonight, percent] |
| 176 | Lyndon B. Johnson | January 17, 1968 | [programs, million, budget, tonight, billion] |
| 177 | Lyndon B. Johnson | January 14, 1969 | [americans, program, billion, budget, tonight] |
| 178 | Richard Nixon | January 22, 1970 | [billion, percent, america, today, programs] |
| 179 | Richard Nixon | January 22, 1971 | [federal, americans, budget, tonight, let] |
| 180 | Richard Nixon | January 20, 1972 | [america, program, programs, today, help] |
| 181 | Richard Nixon | February 2, 1973 | [economic, help, americans, working, programs] |
| 182 | Richard Nixon | January 30, 1974 | [program, americans, today, energy, tonight] |
| 183 | Gerald R. Ford | January 15, 1975 | [program, percent, billion, programs, energy] |
| 184 | Gerald R. Ford | January 19, 1976 | [federal, americans, budget, jobs, programs] |
| 185 | Gerald R. Ford | January 12, 1977 | [programs, today, percent, jobs, energy] |
| 186 | Jimmy Carter | January 19, 1978 | [cannot, economic, tonight, jobs, it's] |
| 187 | Jimmy Carter | January 25, 1979 | [cannot, budget, tonight, americans, it's] |
| 188 | Jimmy Carter | January 21, 1980 | [help, america, energy, tonight, it's] |
| 189 | Jimmy Carter | January 16, 1981 | [percent, economic, energy, program, programs] |
| 190 | Ronald Reagan | January 26, 1982 | [jobs, help, program, billion, programs] |
| 191 | Ronald Reagan | January 25, 1983 | [problems, programs, americans, economic, perc... |
| 192 | Ronald Reagan | January 25, 1984 | [budget, help, americans, tonight, it's] |
| 193 | Ronald Reagan | February 6, 1985 | [help, tax, jobs, tonight, it's] |
| 194 | Ronald Reagan | February 4, 1986 | [america, cannot, it's, budget, tonight] |
| 195 | Ronald Reagan | January 27, 1987 | [percent, let, budget, tonight, it's] |
| 196 | Ronald Reagan | January 25, 1988 | [let, americans, it's, budget, tonight] |
| 197 | George H.W. Bush | February 9, 1989 | [help, ask, it's, budget, tonight] |
| 198 | George H.W. Bush | January 31, 1990 | [percent, budget, today, tonight, it's] |
| 199 | George H.W. Bush | January 29, 1991 | [jobs, budget, americans, know, tonight] |
| 200 | George H.W. Bush | January 28, 1992 | [know, get, tonight, help, it's] |
| 201 | William J. Clinton | February 17, 1993 | [tax, budget, percent, tonight, jobs] |
| 202 | William J. Clinton | January 25, 1994 | [americans, it's, health, get, jobs] |
| 203 | William J. Clinton | January 24, 1995 | [jobs, americans, get, tonight, it's] |
| 204 | William J. Clinton | January 23, 1996 | [tonight, families, working, americans, children] |
| 205 | William J. Clinton | February 4, 1997 | [america, children, budget, americans, tonight] |
| 206 | William J. Clinton | January 27, 1998 | [ask, americans, children, help, tonight] |
| 207 | William J. Clinton | January 19, 1999 | [children, budget, help, americans, tonight] |
| 208 | William J. Clinton | January 27, 2000 | [families, help, children, americans, tonight] |
| 209 | George W. Bush | February 27, 2001 | [help, tax, percent, tonight, budget] |
| 210 | George W. Bush | September 20, 2001 | [freedom, america, ask, americans, tonight] |
| 211 | George W. Bush | January 29, 2002 | [americans, budget, tonight, america, jobs] |
| 212 | George W. Bush | January 28, 2003 | [america, help, million, americans, tonight] |
| 213 | George W. Bush | January 20, 2004 | [children, america, americans, help, tonight] |
| 214 | George W. Bush | February 2, 2005 | [freedom, tonight, help, social, americans] |
| 215 | George W. Bush | January 31, 2006 | [reform, jobs, americans, america, tonight] |
| 216 | George W. Bush | January 23, 2007 | [children, health, americans, tonight, help] |
| 217 | George W. Bush | January 29, 2008 | [america, americans, trust, tonight, help] |
| 218 | Barack Obama | February 24, 2009 | [know, budget, jobs, tonight, it's] |
| 219 | Barack Obama | January 27, 2010 | [get, tonight, americans, jobs, it's] |
| 220 | Barack Obama | January 25, 2011 | [percent, get, tonight, jobs, it's] |
| 221 | Barack Obama | January 24, 2012 | [americans, tonight, get, it's, jobs] |
| 222 | Barack Obama | February 12, 2013 | [families, it's, get, tonight, jobs] |
| 223 | Barack Obama | January 28, 2014 | [get, tonight, help, it's, jobs] |
| 224 | Barack Obama | January 20, 2015 | [families, americans, tonight, jobs, it's] |
| 225 | Barack Obama | January 12, 2016 | [tonight, jobs, americans, get, it's] |
| 226 | Donald J. Trump | February 27, 2017 | [america, jobs, americans, it's, tonight] |
| 227 | Donald J. Trump | January 30, 2018 | [tax, get, it's, americans, tonight] |
| 228 | Donald J. Trump | February 5, 2019 | [get, jobs, americans, it's, tonight] |
| 229 | Donald J. Trump | February 4, 2020 | [jobs, it's, americans, percent, tonight] |
| 230 | Joseph R. Biden Jr. | April 28, 2021 | [get, americans, percent, jobs, it's] |
| 231 | Joseph R. Biden Jr. | March 1, 2022 | [let, jobs, americans, get, tonight] |
| 232 | Joseph R. Biden Jr. | February 7, 2023 | [down, percent, jobs, tonight, it's] |
Let's try it and see what happens.
tfidf_nl_dict = {}
tf_denom = speeches_df['contents'].str.split().str.len()
for word in unique_words:
re_pat = fr' {word} ' # Imperfect pattern for speed.
tf = speeches_df['contents'].str.count(re_pat) / tf_denom
idf_nl = len(speeches_df) / speeches_df['contents'].str.contains(re_pat).sum()
tfidf_nl_dict[word] = tf * idf_nl
tfidf_nl = pd.DataFrame(tfidf_nl_dict)
tfidf_nl.head()
| the | of | to | and | in | a | that | for | be | our | ... | desire | call | submitted | increasing | months | point | trust | throughout | set | object | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.089073 | 0.063361 | 0.051423 | 0.037649 | 0.018365 | 0.019284 | 0.013774 | 0.006428 | 0.018365 | 0.009183 | ... | 0.000000 | 0.001313 | 0.000000 | 0.001389 | 0.0 | 0.0 | 0.001465 | 0.000000 | 0.000000 | 0.005783 |
| 1 | 0.086957 | 0.063435 | 0.034925 | 0.032074 | 0.019244 | 0.014968 | 0.012117 | 0.011404 | 0.012830 | 0.012117 | ... | 0.000000 | 0.001019 | 0.001318 | 0.000000 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.000000 | 0.002992 |
| 2 | 0.105035 | 0.069010 | 0.038194 | 0.031684 | 0.017795 | 0.018229 | 0.013889 | 0.009549 | 0.014757 | 0.002170 | ... | 0.000000 | 0.000000 | 0.000803 | 0.000657 | 0.0 | 0.0 | 0.001385 | 0.000000 | 0.001297 | 0.001822 |
| 3 | 0.093212 | 0.066444 | 0.042065 | 0.026769 | 0.022945 | 0.015296 | 0.011472 | 0.014340 | 0.013862 | 0.005258 | ... | 0.000870 | 0.000683 | 0.000000 | 0.000000 | 0.0 | 0.0 | 0.002289 | 0.000753 | 0.000000 | 0.002007 |
| 4 | 0.091603 | 0.067176 | 0.037659 | 0.024936 | 0.013232 | 0.017303 | 0.006107 | 0.011705 | 0.021883 | 0.008142 | ... | 0.001853 | 0.000000 | 0.000000 | 0.000000 | 0.0 | 0.0 | 0.000812 | 0.001602 | 0.000000 | 0.001068 |
5 rows × 500 columns
keywords_nl = tfidf_nl.apply(five_largest, axis=1)
keywords_nl_df = pd.concat([
speeches_df['president'],
speeches_df['date'],
keywords_nl
], axis=1)
keywords_nl_df
| president | date | 0 | |
|---|---|---|---|
| 0 | George Washington | January 8, 1790 | [a, and, to, of, the] |
| 1 | George Washington | December 8, 1790 | [in, and, to, of, the] |
| 2 | George Washington | October 25, 1791 | [a, and, to, of, the] |
| 3 | George Washington | November 6, 1792 | [in, and, to, of, the] |
| 4 | George Washington | December 3, 1793 | [be, and, to, of, the] |
| ... | ... | ... | ... |
| 228 | Donald J. Trump | February 5, 2019 | [in, of, to, and, the] |
| 229 | Donald J. Trump | February 4, 2020 | [in, of, to, and, the] |
| 230 | Joseph R. Biden Jr. | April 28, 2021 | [of, it's, and, to, the] |
| 231 | Joseph R. Biden Jr. | March 1, 2022 | [we, of, to, and, the] |
| 232 | Joseph R. Biden Jr. | February 7, 2023 | [a, of, and, to, the] |
233 rows × 3 columns
(1000 / 999)
1.001001001001001
np.log(1000 / 999)
0.001000500333583622
(50 / 2)
25.0
(500 / 2)
250.0
np.log(50 / 2)
3.2188758248682006
np.log(500 / 2)
5.521460917862246
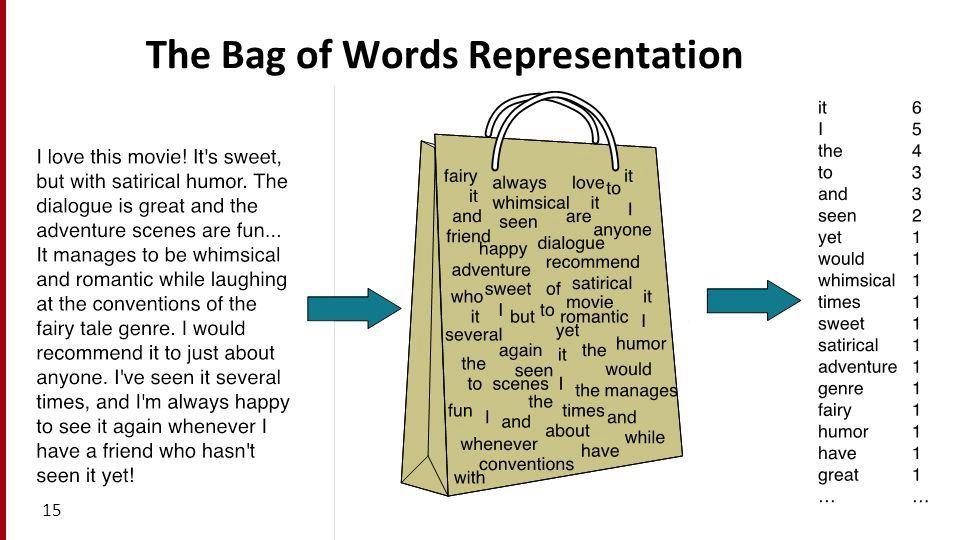
'deputy fire chief', into feature vectors, is to count the number of occurrences of each word in the document, ignoring order. This is done using the bag of words model.Modeling and feature engineering.