Lecture 22 – Pipelines, Generalization

DSC 80, Winter 2023

📣 Announcements

Agenda

The modeling process

The modeling process

  1. Create (engineer) features to best reflect the "meaning" behind data.
  1. Choose a model that is appropriate to capture the relationships between features ($X$) and the target/response ($y$).
  1. Select a loss function and fit the model (i.e., determine $w^*$).
  1. Evaluate the model (e.g. using RMSE or $R^2$).

We can perform all of the above directly in sklearn!

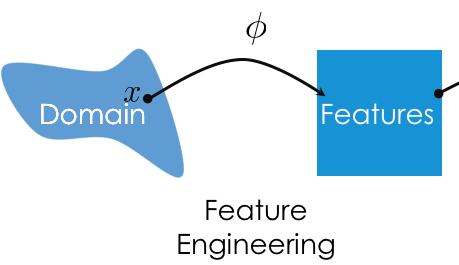
preprocessing and linear_models

For the feature engineering step of the modeling pipeline, we will use sklearn's preprocessing module.

For the model creation step of the modeling pipeline, we will use sklearn's linear_model module, as we've already seen. linear_model.LinearRegression is an example of an estimator class.

Transformers in sklearn

Transformer classes

Case study: Restaurant tips 🧑‍🍳

We'll continue working with our trusty tips dataset.

Example transformer: Binarizer

The Binarizer transformer allows us to map a quantitative sequence to a sequence of 1s and 0s, depending on whether values are above or below a threshold.

Property Example Description
Initialize with parameters binar = Binarizer(thresh) set x=1 if x > thresh, else 0
Transform data in a dataset feat = binar.transform(data) Binarize all columns in data

First, we need to import the relevant class from sklearn.preprocessing. (Tip: import just the relevant classes you need from sklearn.)

Let's try binarizing 'total_bill'. We'll say a "large" bill is one that is strictly greater than \$20.

First, we initialize a Binarizer object with the threshold we want.

Then, we call bi's transform method and pass it the data we'd like to transform. Note that its input and output are both 2D.

Example transformer: StdScaler

$$z(x_i) = \frac{x_i - \text{mean of } x}{\text{SD of } x}$$

Example transformer: StdScaler

It only makes sense to standardize the already-quantitative features of tips, so let's select just those.

Let's initialize a StandardScaler object.

Note that the following does not work! The error message is very helpful.

Instead, we need to first call the fit method on stdscaler.

Now, transform will work.

We can also access the mean and variance stdscaler computed for each column:

Note that we can call transform on DataFrames other than tips_quant. We will do this often – fit a transformer on one dataset (training data) and use it to transform other datasets (test data).

StdScaler summary

Property Example Description
Initialize with parameters stdscaler = StandardScaler() z-score the data (no parameters)
Fit the transformer stdscaler.fit(X) Compute the mean and SD of X
Transform data in a dataset feat = stdscaler.transform(X_new) z-score X_new with mean and SD of X

Example transformer: OneHotEncoder

Let's keep just the categorical columns in tips.

Like StdScaler, we will need to fit our OneHotEncoder transformer before it can transform anything.

We can look at the unique values (i.e. categories) in each column by using the categories_ attribute:

Since the resulting matrix is sparse – most of its elements are 0 – sklearn uses a more efficient representation than a regular numpy array. That's no issue, though:

Notice that the column names from tips_cat are no longer stored anywhere (remember, fit converts the input to a numpy array before proceeding).

We can use the get_feature_names method on ohe to access the names of the one-hot-encoded columns, though:

Pipelines


So far, we've used transformers for feature engineering and models for prediction. We can combine these steps into a single Pipeline.

Pipelines in sklearn

Our first Pipeline

Let's build a Pipeline that:

Now that pl is instantiated, we fit it the same way we would fit the individual steps.

Now, to make predictions using raw data, all we need to do is use pl.predict:

pl performs both feature transformation and prediction with just a single call to predict!

We can access individual "steps" of a Pipeline through the named_steps attribute:

pl also has a score method, the same way a fit LinearRegression instance does:

More sophisticated Pipelines

Planning our first ColumnTransformer

Let's perform different transformations on the quantitative and categorical features of tips (note that we are not transforming 'tip').

size x0_Female x0_Male x1_No x1_Yes x2_Fri x2_Sat x2_Sun x2_Thur x3_Dinner x3_Lunch total_bill
0 0 1.0 0.0 1.0 0.0 0.0 0.0 1.0 0.0 1.0 0.0 16.99
1 1 0.0 1.0 1.0 0.0 0.0 0.0 1.0 0.0 1.0 0.0 10.34
2 1 0.0 1.0 1.0 0.0 0.0 0.0 1.0 0.0 1.0 0.0 21.01
3 0 0.0 1.0 1.0 0.0 0.0 0.0 1.0 0.0 1.0 0.0 23.68
4 1 1.0 0.0 1.0 0.0 0.0 0.0 1.0 0.0 1.0 0.0 24.59

Building a Pipeline using a ColumnTransformer

Let's start by creating our ColumnTransformer.

Now, let's create a Pipeline using preproc as a transformer, and fit it:

Prediction is as easy as calling predict:

We can even call each transformer in pl['preprocessor'] individually to re-create the transformed DataFrame. (There's no practical reason to do this, it's more for illustration.)

Aside: FunctionTransformer

A transformer you'll often use as part of a ColumnTransformer is the FunctionTransformer, which enables you to use your own functions on entire columns. Think of it as the sklearn equivalent of apply.

Summary: Pipelines

Generalization

Motivation

Evaluating the quality of a model

Example: Overfitting and underfitting

Let's collect two samples $\{(x_i, y_i)\}$ from the same data generating process.

For now, let's just look at Sample 1. The relationship between $x$ and $y$ is roughly cubic; that is, $y \approx x^3$ (remember, in reality, you won't get to see the DGP).

Polynomial regression

Let's fit three polynomial models on Sample 1:

The PolynomialFeatures transformer will be helpful here.

Below, we look at our three models' predictions on Sample 1 (which they were trained on).

The degree 25 polynomial has the lowest RMSE on Sample 1.

How do the same fit polynomials look on Sample 2?

What if we fit a degree 1, degree 3, and degree 25 polynomial on Sample 2 as well?

Key idea: Degree 25 polynomials seem to vary more when trained on different samples than degree 3 and 1 polynomials do.

Bias and variance

The training data we have access to is a sample from the DGP. We are concerned with our model's ability to generalize and work well on different datasets drawn from the same DGP.

Suppose we fit a model $H$ (e.g. a degree 3 polynomial) on several different datasets from a DGP. There are three sources of error that arise:

Here, suppose:

We'd like our models to be in the top left, but in practice that's hard to achieve!

Summary, next time

Summary

Next time

How do we choose the right model complexity, so that our model has the right "balance" between bias and variance?