from dsc80_utils import *

Lecture 6 – Hypothesis Testing

DSC 80, Spring 2024

In case you need a review from DSC 10, I've made a Pre-Lecture Review for this lecture.

Announcements 📣

• Project 1 is due tomorrow, April 19th.
• Lab 3 is due on Wed, Apr 24th.
• DSC undergraduate town hall is Monday, Apr 22 1-3pm in the HDSI 1st floor MPR.
  • Q&A with faculty about undergrad program + mixer with faculty afterwards.
  • Cookies and snacks provided!

Agenda 📆

• Data scope.
• Overview of hypothesis testing.
• Example: Total variation distance.
• Permutation testing.
  • Example: Birth weight and smoking 🚬.
  • Example (that you'll read on your own): Permutation testing meets TVD.

Why are we learning hypothesis testing again?

You may say,

Didn't we already learn this in DSC 10?

Yes, but:

• It's an important concept, but one that's confusing to understand the first time you learn about it.

• In addition, in order to properly handle missing values (next lecture), we need to learn how to identify different missingness mechanisms. Doing so requires performing a hypothesis test.

Data scope

Where are we in the data science lifecycle?

Hypothesis testing is a tool for helping us understand the world (some population), given our understanding of the data (some sample).

Data scope

• Statistical inference: The practice of drawing conclusions about a population, given a sample.

• Target population: All elements of the population you ultimately want to draw conclusions about.

• Access frame: All elements that are accessible for you for measurement and observation.

• Sample: The subset of the access frame that you actually measured / observed.

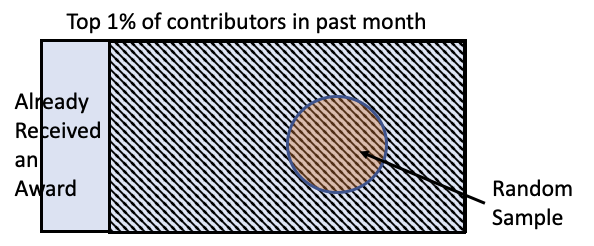
Example: Wikipedia awards

A 2012 paper asked:

If we give awards to Wikipedia contributors, will they contribute more?

To test this question, they took the top 1% of all Wikipedia contributors, excluded those who already received an award, and then took a random sample of 200 contributors.

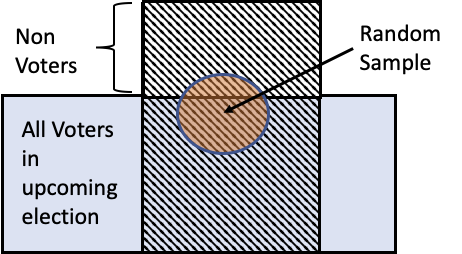
Example: Who will win the election?

In the 2016 US Presidental Election, most pollsters predicted Clinton to win over Trump, even though Trump ultimately won.

To poll, they randomly selected potential voters and asked them a question over the phone.

🔑 Key Idea: Random samples look like the access frame they were sampled from!

• This enables statistical inference!

• But keep in mind, random samples look like their access frame which can be different than the population itself.

Sampling in practice

In DSC 10, you used a few key functions/methods to draw samples from populations.

• To draw samples from a known sequence (e.g. array or Series), you used np.random.choice.

names = np.load(Path('data') / 'names.npy', allow_pickle=True)

# By default, the sampling is done WITH replacement.
np.random.choice(names, 10)

array(['Lin', 'Yeogyeong', 'Subika', 'Jesse', 'Aakash', 'Chenlong',
       'David', 'Ethan', 'Seanna', 'Ailinna'], dtype=object)

# To sample WITHOUT replacement, set replace=False.
# This is known as "simple random sampling."
np.random.choice(names, 10, replace=False)

array(['Kening', 'Ethan', 'Diya', 'Seanna', 'Colin', 'Zening',
       'Stephanie', 'Jiaye', 'Dylan', 'Jessica'], dtype=object)

• The DataFrame .sample method also allowed you to draw samples from a known sequence.

# Samples WITHOUT replacement by default (the opposite of np.random.choice).
pd.DataFrame(names, columns=['name']).sample(10)

	name
105	Yiran
48	Kailey
76	Niha
...	...
21	David
24	Diego
26	Dylan

10 rows × 1 columns

• To sample from a categorical distribution, you used np.random.multinomial. Note that in the cell below, we don't see array([50, 50]) every time, and that's due to randomness!

# Draws 100 elements from a population in which 50% are group 0 and 50% are group 1.
# This sampling is done WITH replacement.
# In other words, each sampled element has a 50% chance of being group 0 and a 50% chance of being group 1.
np.random.multinomial(100, [0.5, 0.5])

array([50, 50])

Overview of hypothesis testing

What problem does hypothesis testing solve?

Suppose we've performed an experiment, or identified something interesting in our data.

• Say we've created a new vaccine.

• To assess its efficiency, we give one group the vaccine, and another a placebo.

• We notice that the flu rate among those who received the vaccine is lower than among those who received the placebo (i.e. didn't receive the vaccine).

• One possibility: the vaccine doesn't actually do anything, and by chance, those with the vaccine happened to have a lower flu rate.

• Another possibility: receiving the vaccine made a difference – the flu rate among those who received the vaccine is lower than we'd expect due to random chance.

• Hypothesis testing allows us to determine whether an observation is "significant."

Why hypothesis testing is difficult to learn

• It's like "[proof by contradiction](https://brilliant.org/wiki/contradiction/#:~:text=Proof%20by%20contradiction%20(also%20known,the%20opposite%20must%20be%20true.)."

• If I want to show that my vaccine works, I consider a world where it doesn't (null hypothesis).

• Then, I show that under the null hypothesis my data would be very unlikely.

• Why go through these mental hurdles? Showing something is not true is usually easier than showing something is true!

The hypothesis testing "recipe"

Faced with a question about the data raised by an observation...

1. Decide on null and alternate hypotheses.

   • The null hypothesis should be a well-defined probability model that reflects the baseline you want to compare against.
   • The alternative hypothesis should be the "alternate reality" that you suspect may be true.

2. Decide on a test statistic, such that a large observed statistic would point to one hypothesis and a small observed statistic would point to the other.

3. Compute an empirical distribution of the test statistic under the null by drawing samples from the null hypothesis' probability model.

4. Assess whether the observed test statistic is consistent with the empirical distribution of the test statistic by computing a p-value.

Question 🤔 (Answer at q.dsc80.com)

Complete Problem 10 from the Spring 2023 DSC 10 Final Exam with a neighbor. Submit your answers to q.dsc80.com, then reveal the answers.

Example: Total variation distance

Ethnic distribution of California vs. UCSD

The DataFrame below contains the ethnic breakdown of the state as a whole (source) and UCSD as of 2016 (source).

eth = pd.DataFrame(
    [['Asian', 0.15, 0.51],
     ['Black', 0.05, 0.02],
     ['Latino', 0.39, 0.16],
     ['White', 0.35, 0.2],
     ['Other', 0.06, 0.11]],
    columns=['Ethnicity', 'California', 'UCSD']
).set_index('Ethnicity')

eth

	California	UCSD
Ethnicity
Asian	0.15	0.51
Black	0.05	0.02
Latino	0.39	0.16
White	0.35	0.20
Other	0.06	0.11

• The two distributions above are clearly different.

• One possibility: UCSD students do look like a random sample of California residents, and the distributions above look different purely due to random chance.

• Another possibility: UCSD students don't look like a random sample of California residents, because the distributions above look too different.

Is the difference between the two distributions significant?

Let's establish our hypotheses.

• Null Hypothesis: UCSD students were selected at random from the population of California residents.
• Alternative Hypothesis: UCSD students were not selected at random from the population of California residents.
• Observation: Ethnic distribution of UCSD students.
• Test Statistic: We need a way of quantifying how different two categorical distributions are.

eth.plot(kind='barh', title='Ethnic Distribution of California and UCSD', barmode='group')

How can we summarize the difference, or distance, between these two distributions using just a single number?

Total variation distance

The total variation distance (TVD) is a test statistic that describes the distance between two categorical distributions.

If $A = [a_1, a_2, ..., a_k]$ and $B = [b_1, b_2, ..., b_k]$ are both categorical distributions, then the TVD between $A$ and $B$ is

$$\text{TVD}(A, B) = \frac{1}{2} \sum_{i = 1}^k \big|a_i - b_i\big|$$

Let's compute the TVD between UCSD's ethnic distribution and California's ethnic distribution. We could define a function to do this (and you can use this in assignments):

def tvd(dist1, dist2):
    return np.abs(dist1 - dist2).sum() / 2

But let's try and work on the eth DataFrame directly, using the diff method.

# The diff method finds the differences of consecutive elements in a Series.
pd.Series([4, 5, -2]).diff()

0    NaN
1    1.0
2   -7.0
dtype: float64

observed_tvd = eth.diff(axis=1).abs().sum().iloc[1] / 2
observed_tvd

0.41000000000000003

The issue is we don't know whether this is a large value or a small value – we don't know where it lies in the distribution of TVDs under the null.

The plan

To conduct our hypothesis test, we will:

• Repeatedly generate samples of size 30,000 (the number of UCSD students) from the ethnic distribution of all of California.

• Each time, compute the TVD between the simulated distribution and California's distribution.

• This will generate an empirical distribution of TVDs, under the null.

• Finally, determine whether the observed TVD (0.41) is consistent with the empirical distribution of TVDs.

Generating one random sample

Again, to sample from a categorical distribution, we use np.random.multinomial.

Important: We must sample from the "population" distribution here, which is the ethnic distribution of everyone in California.

# Number of students at UCSD in this example.
N_STUDENTS = 30_000

eth['California']

Ethnicity
Asian     0.15
Black     0.05
Latino    0.39
White     0.35
Other     0.06
Name: California, dtype: float64

np.random.multinomial(N_STUDENTS, eth['California'])

array([ 4446,  1517, 11713, 10613,  1711])

np.random.multinomial(N_STUDENTS, eth['California']) / N_STUDENTS

array([0.15, 0.05, 0.39, 0.35, 0.06])

Generating many random samples and computing TVDs, without a for-loop

We could write a for-loop to repeat the process on the previous slide repeatedly (and you can in labs and projects). However, the Pre-Lecture Review told us about the size argument in np.random.multinomial, so let's use that here.

eth_draws = np.random.multinomial(N_STUDENTS, eth['California'], size=100_000) / N_STUDENTS
eth_draws

array([[0.15, 0.05, 0.39, 0.35, 0.06],
       [0.15, 0.05, 0.39, 0.35, 0.06],
       [0.15, 0.05, 0.39, 0.35, 0.06],
       ...,
       [0.15, 0.05, 0.39, 0.35, 0.06],
       [0.15, 0.05, 0.39, 0.35, 0.06],
       [0.15, 0.05, 0.39, 0.35, 0.06]])

eth_draws.shape

(100000, 5)

Notice that each row of eth_draws sums to 1, because each row is a simulated categorical distribution.

# The values here appear rounded.
tvds = np.abs(eth_draws - eth['California'].to_numpy()).sum(axis=1) / 2
tvds

array([0., 0., 0., ..., 0., 0., 0.])

Visualizing the empirical distribution of the test statistic

observed_tvd

0.41000000000000003

fig = px.histogram(pd.DataFrame(tvds), x=0, nbins=20, histnorm='probability', 
                   title='Empirical Distribution of the TVD')
fig

(np.array(tvds) >= observed_tvd).mean()

0.0

No, there's not a mistake in our code!

Conclusion

• The chance that the observed TVD came from the distribution of TVDs under the null is essentially 0.
• This matches our intuition from the start – the two distributions looked very different to begin with. But now we're quite sure the difference can't be explained solely due to sampling variation.

Summary of the method

To assess whether an "observed sample" was drawn randomly from a known categorical distribution:

• Use the TVD as the test statistic because it measures the distance between two categorical distributions.
• Sample at random from the population. Compute the TVD between each random sample and the known distribution to get an idea for what reasonable deviations from the eligible pool look like. Repeat this process many, many times.
• Compare:
  • the empirical distribution of TVDs, with
  • the observed TVD from the sample.

Aside

• It was probably obvious that the difference is significant even before running a hypothesis test.

• Why? There are 30,000 students. Such a difference in proportion is unlikely to be due to random chance – there's something more systematic at play.

• But what if N_STUDENTS = 300, N_STUDENTS = 30, or N_STUDENTS=3?

eth

	California	UCSD
Ethnicity
Asian	0.15	0.51
Black	0.05	0.02
Latino	0.39	0.16
White	0.35	0.20
Other	0.06	0.11

def ethnicity_test(N_STUDENTS):
    eth_draws = np.random.multinomial(N_STUDENTS, eth['California'], size=100_000) / N_STUDENTS
    tvds = np.sum(np.abs(eth_draws - eth['California'].to_numpy()), axis=1) / 2
    return (np.array(tvds) >= observed_tvd).mean()

for i in range(1, 9):
    N_STUDENTS = 2 ** i
    print(f'With {N_STUDENTS} students, the p-value is {ethnicity_test(N_STUDENTS)}.')

With 2 students, the p-value is 0.72779.
With 4 students, the p-value is 0.3063.
With 8 students, the p-value is 0.08288.
With 16 students, the p-value is 0.00365.
With 32 students, the p-value is 2e-05.
With 64 students, the p-value is 0.0.
With 128 students, the p-value is 0.0.
With 256 students, the p-value is 0.0.

Question 🤔 (Answer at q.dsc80.com)

What questions do you have?

Permutation testing

Hypothesis testing vs. permutation testing

• So far, we've used hypothesis tests to answer questions of the form:

I know the population distribution, and I have one sample. Is this sample a likely draw from the population?

• Next, we want to consider questions of the form:

I have two samples, but no information about any population distributions. Do these samples look like they were drawn from different populations? That is, do these two samples look "different"?

Hypothesis testing vs. permutation testing

This framework requires us to be able to draw samples from the baseline population – but what if we don't know that population?

Example: Birth weight and smoking 🚬

For familiarity, we'll start with an example from DSC 10. This means we'll move quickly!

Let's start by loading in the data. Each row corresponds to a mother/baby pair.

baby = pd.read_csv(Path('data') / 'babyweights.csv')
baby

	Birth Weight	Gestational Days	Maternal Age	Maternal Height	Maternal Pregnancy Weight	Maternal Smoker
0	120	284	27	62	100	False
1	113	282	33	64	135	False
2	128	279	28	64	115	True
...	...	...	...	...	...	...
1171	130	291	30	65	150	True
1172	125	281	21	65	110	False
1173	117	297	38	65	129	False

1174 rows × 6 columns

We're only interested in the 'Birth Weight' and 'Maternal Smoker' columns.

baby = baby[['Maternal Smoker', 'Birth Weight']]
baby.head()

	Maternal Smoker	Birth Weight
0	False	120
1	False	113
2	True	128
3	True	108
4	False	136

Note that there are two samples:

• Birth weights of smokers' babies (rows where 'Maternal Smoker' is True).
• Birth weights of non-smokers' babies (rows where 'Maternal Smoker' is False).

Exploratory data analysis

How many babies are in each group? What is the average birth weight within each group?

baby.groupby('Maternal Smoker')['Birth Weight'].agg(['mean', 'count'])

	mean	count
Maternal Smoker
False	123.09	715
True	113.82	459

Note that 16 ounces are in 1 pound, so the above weights are ~7-8 pounds.

Visualizing birth weight distributions

Below, we draw the distributions of both sets of birth weights.

fig = px.histogram(baby, color='Maternal Smoker', histnorm='probability', marginal='box', 
                   title="Birth Weight by Mother's Smoking Status", barmode='overlay', opacity=0.7)
fig

There appears to be a difference, but can it be attributed to random chance?

Null hypothesis: birth weights come from the same distribution

• Our null hypothesis states that "smoker" / "non-smoker" labels have no relationship to birth weight.
• In other words, the "smoker" / "non-smoker" labels may well have been assigned at random.

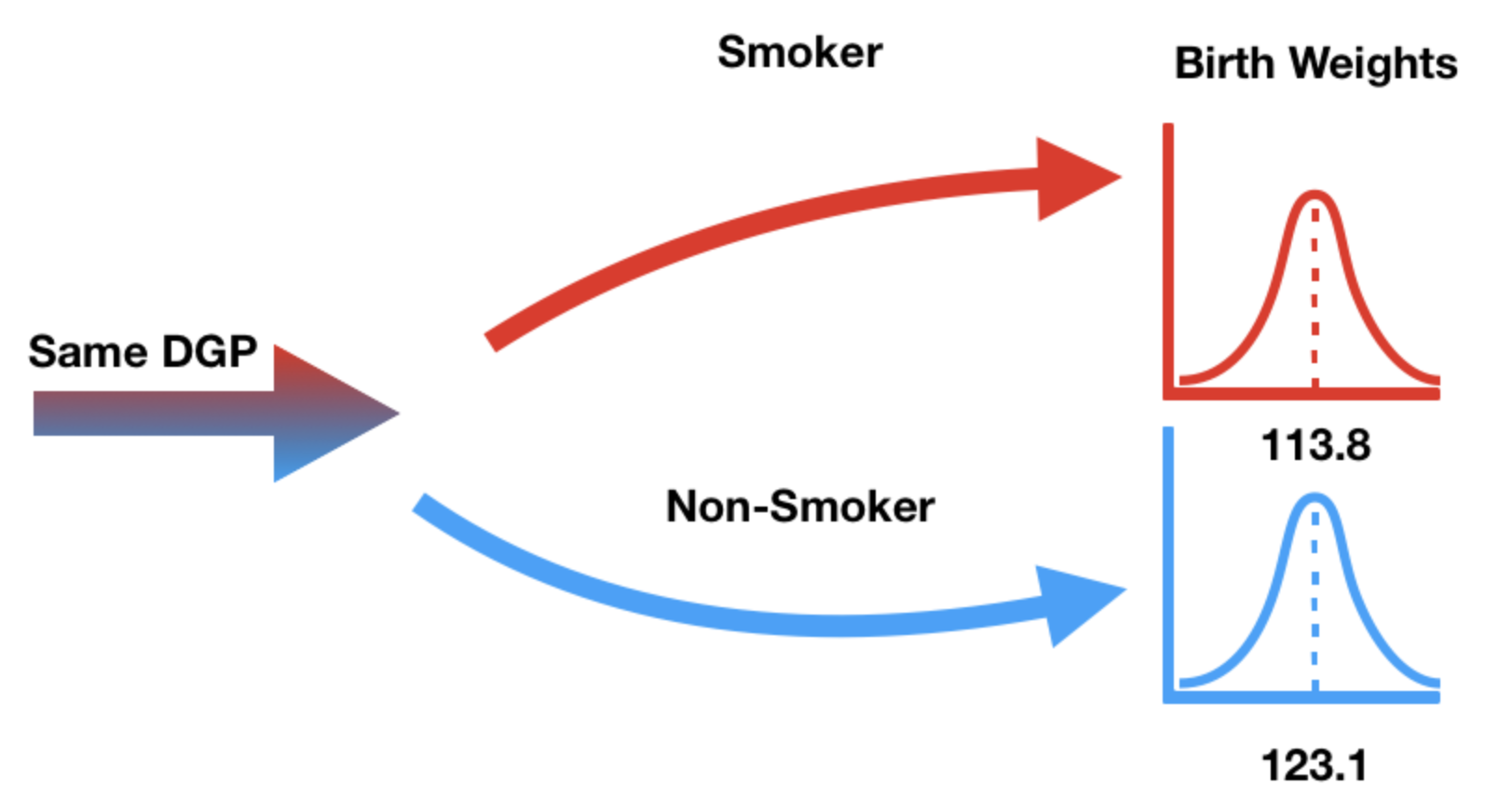
DGP stands for "data generating process" – think of this as another word for population.

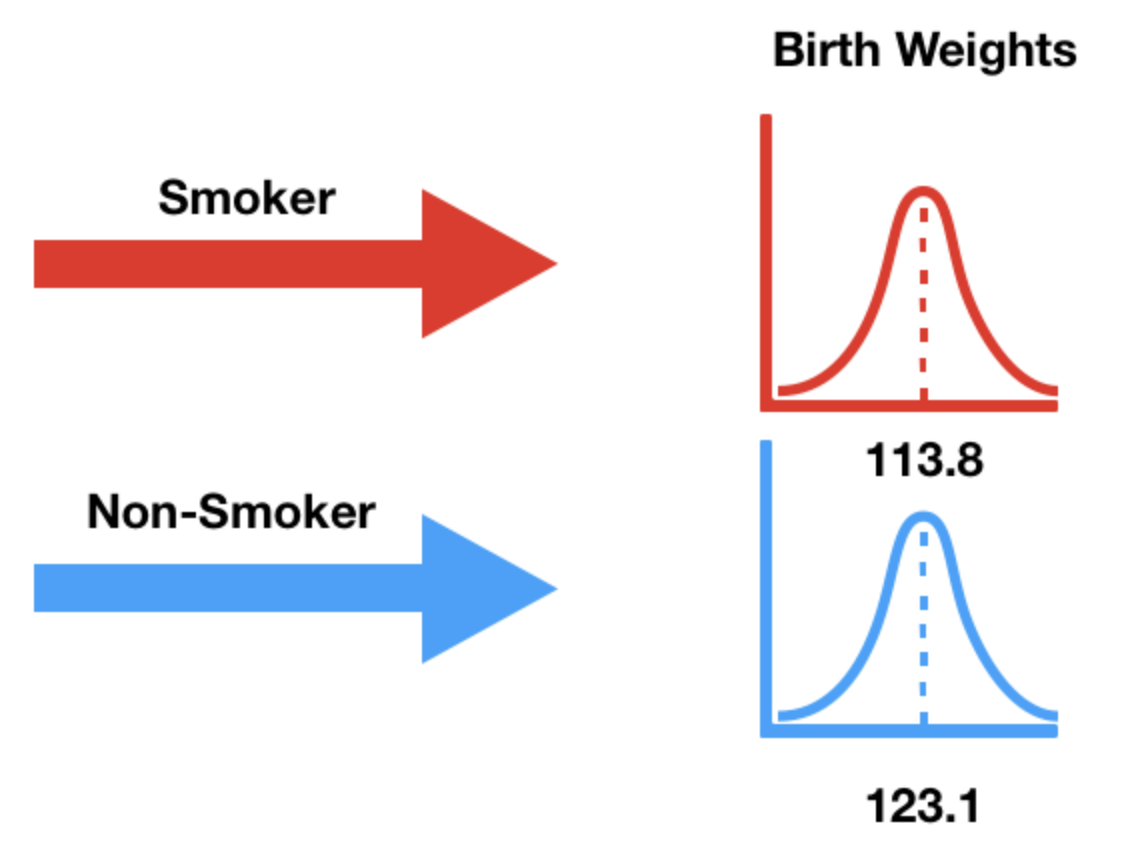
Alternative hypothesis: birth weights come from different distributions

• Our alternative hypothesis states that the birth weights weights of smokers' babies and non-smokers' babies come from different population distributions.
  • That is, they come from different data generating processes.
• It also states that smokers' babies weigh significantly less.

Choosing a test statistic

We need a test statistic that can measure how different two numerical distributions are.

fig = px.histogram(baby, color='Maternal Smoker', histnorm='probability', marginal='box', 
                   title="Birth Weight by Mother's Smoking Status", barmode='overlay', opacity=0.7)
fig

Easiest solution: Difference in group means.

Difference in group means

We'll choose our test statistic to be:

$$\text{mean weight of smokers' babies} - \text{mean weight of non-smokers' babies}$$

We could also compute the non-smokers' mean minus the smokers' mean, too.

group_means = baby.groupby('Maternal Smoker')['Birth Weight'].mean()
group_means

Maternal Smoker
False    123.09
True     113.82
Name: Birth Weight, dtype: float64

Use loc with group_means to compute the difference in group means.

group_means.loc[True] - group_means.loc[False]

-9.266142572024918

Hypothesis test setup

• Null Hypothesis: In the population, birth weights of smokers' babies and non-smokers' babies have the same distribution, and the observed differences in our samples are due to random chance.

• Alternative Hypothesis: In the population, smokers' babies have lower birth weights than non-smokers' babies, on average. The observed difference in our samples cannot be explained by random chance alone.

• Test Statistic: Difference in group means.

$$\text{mean weight of smokers' babies} - \text{mean weight of non-smokers' babies}$$

• Issue: We don't know what the population distribution actually is – so how do we draw samples from it?
  • This is different from the coin flipping, and the California ethnicity examples, because there the null hypotheses were well-defined probability models.

Implications of the null hypothesis

• Under the null hypothesis, both groups are sampled from the same distribution.
• If this is true, then the group label – 'Maternal Smoker' – has no effect on the birth weight.
• In our dataset, we saw one assignment of True or False to each baby.

baby.head()

	Maternal Smoker	Birth Weight
0	False	120
1	False	113
2	True	128
3	True	108
4	False	136

• Under the null hypothesis, we were just as likely to see any other assignment.

Permutation tests

• In a permutation test, we generate new data by shuffling group labels.

  • In our current example, this involves randomly assigning babies to True or False, while keeping the same number of Trues and Falses as we started with.

• On each shuffle, we'll compute our test statistic (difference in group means).

• If we shuffle many times and compute our test statistic each time, we will approximate the distribution of the test statistic.

• We can them compare our observed statistic to this distribution, as in any other hypothesis test.

Shuffling

• Our goal, by shuffling, is to randomly assign values in the 'Maternal Smoker' column to values in the 'Birth Weight' column.

• We can do this by shuffling either column independently.

• Easiest solution: np.random.permutation.

  • We could also use df.sample, but it's more complicated (and slower).

np.random.permutation(baby['Birth Weight'])

array([144, 113, 115, ..., 109,  94, 132])

with_shuffled = baby.assign(Shuffled_Weights=np.random.permutation(baby['Birth Weight']))
with_shuffled.head()

	Maternal Smoker	Birth Weight	Shuffled_Weights
0	False	120	134
1	False	113	106
2	True	128	112
3	True	108	115
4	False	136	129

Now, we have a new sample of smokers' weights, and a new sample of non-smokers' weights!

Effectively, we took a random sample of 459 'Birth Weights' and assigned them to the smokers' group, and the remaining 715 to the non-smokers' group.

How close are the means of the shuffled groups?

One benefit of shuffling 'Birth Weight' (instead of 'Maternal Smoker') is that grouping by 'Maternal Smoker' allows us to see all of the following information with a single call to groupby.

group_means = with_shuffled.groupby('Maternal Smoker').mean()
group_means

	Birth Weight	Shuffled_Weights
Maternal Smoker
False	123.09	119.29
True	113.82	119.74

Let's visualize both pairs of distributions – what do you notice?

for x in ['Birth Weight', 'Shuffled_Weights']:
    diff = group_means.loc[True, x] - group_means.loc[False, x]
    fig = px.histogram(
        with_shuffled, x=x, color='Maternal Smoker', histnorm='probability', marginal='box', 
        title=f"Using the {x} column <br>(difference in means = {diff:.2f})",
        barmode='overlay', opacity=0.7)
    fig.update_layout(margin=dict(t=60))
    fig.show()

Simulating the empirical distribution of the test statistic

• This was just one random shuffle.

• The question we are trying to answer is, how likely is it that a random shuffle results in two samples where the difference in group means (smoker minus non-smoker) is $\geq$ 9.26?

• To answer this question, we need the distribution of the test statistic. To generate that, we must shuffle many, many times. On each iteration, we must:

  1. Shuffle the weights and store them in a DataFrame.
  2. Compute the test statistic (difference in group means).
  3. Store the result.

n_repetitions = 500

differences = []
for _ in range(n_repetitions):
    
    # Step 1: Shuffle the weights and store them in a DataFrame.
    with_shuffled = baby.assign(Shuffled_Weights=np.random.permutation(baby['Birth Weight']))

    # Step 2: Compute the test statistic.
    # Remember, False (0) comes before True (1),
    # so this computes True - False.
    group_means = (
        with_shuffled
        .groupby('Maternal Smoker')
        .mean()
        .loc[:, 'Shuffled_Weights']
    )
    difference = group_means.loc[True] - group_means.loc[False]
    
    # Step 4: Store the result
    differences.append(difference)
    
differences[:10]

[0.8538994774288824,
 0.8538994774288824,
 -0.2872434754787747,
 0.6857686975334047,
 -0.7415543062601841,
 0.7430047077105826,
 0.07048158812864358,
 0.8646312293371068,
 -0.8166765696177407,
 0.4782881606410996]

We already computed the observed statistic earlier, but we compute it again below to keep all of our calculations together.

mean_weights = baby.groupby('Maternal Smoker')['Birth Weight'].mean()
observed_difference = mean_weights[True] - mean_weights[False]
observed_difference

-9.266142572024918

Conclusion of the test

fig = px.histogram(
    pd.DataFrame(differences), x=0, nbins=50, histnorm='probability', 
    title='Empirical Distribution of the Mean Differences <br> in Birth Weights (Smoker - Non-Smoker)')
fig.add_vline(x=observed_difference, line_color='red')
fig.update_layout(xaxis_range=[-10, 10], margin=dict(t=60))

• Under the null hypothesis, we rarely see differences as large as 9.26 ounces.

• Therefore, we reject the null hypothesis that the two groups come from the same distribution. That is, the difference between the two samples is statistically significant.

⚠️ Caution!

• We cannot conclude that smoking causes lower birth weight!
• This was an observational study; there may be confounding factors.
  • Maybe smokers are more likely to drink caffeine, and caffeine causes lower birth weight.

Hypothesis testing vs. permutation testing

• Permutation tests are hypothesis tests!

• "Standard" hypothesis tests answer questions of the form:

I have a population distribution, and I have one sample. Does this sample look like it was drawn from the population?

• Permutation tests answer questions of the form:

I have two samples, but no information about any population distributions. Do these samples look like they were drawn from the same population? That is, do these two samples look "similar"?

Question 🤔 (Answer at q.dsc80.com)

This question was taken from the Spring 2022 Midterm Exam.

Consider the following pair of hypotheses.

• Null Hypothesis: The average GPA of UC San Diego admits from La Jolla Private is equal to the average GPA of UC San Diego admits from all schools.

• Alternative Hypothesis: The average GPA of UC San Diego admits from La Jolla Private is less than the average GPA of UC San Diego admits from all schools.

What type of test is this?

• A. Standard hypothesis test
• B. Permutation test

Question 🤔 (Answer at q.dsc80.com)

This question was taken from the Spring 2022 Midterm Exam.

Consider the following pair of hypotheses.

• Null Hypothesis: The distribution of admitted, waitlisted, and rejected students at UC San Diego from Warren High is equal to the distribution of admitted, waitlisted, and rejected students at UC San Diego from La Jolla Private.

• Alternative Hypothesis: The distribution of admitted, waitlisted, and rejected students at UC San Diego from Warren High is different from the distribution of admitted, waitlisted, and rejected students at UC San Diego from La Jolla Private.

What type of test is this?

• A. Standard hypothesis test
• B. Permutation test

Permutation testing meets TVD

Note: This section has another hypothesis testing example. We might not have time to cover the example in lecture, but you should understand it.

You can also watch this podcast, starting from 4:43 for a walkthrough.

Example: Married vs. unmarried couples

• We will use data from a study conducted in 2010 by the National Center for Family and Marriage Research.
• The data consists of a national random sample of over 1,000 heterosexual couples who were either married or living together but unmarried.
• Each row corresponds to one person (not one couple).

couples = pd.read_csv(Path('data') / 'married_couples.csv')
couples.head()

	hh_id	gender	mar_status	rel_rating	...	education	hh_income	empl_status	hh_internet
0	0	1	1	1	...	12	14	1	1
1	0	2	1	1	...	9	14	1	1
2	1	1	1	1	...	11	15	1	1
3	1	2	1	1	...	9	15	1	1
4	2	1	1	1	...	12	14	1	1

5 rows × 9 columns

# What does this expression compute?
couples['hh_id'].value_counts().value_counts()

2    1033
1       2
Name: hh_id, dtype: int64

We won't use all of the columns in the DataFrame.

couples = couples[['mar_status', 'empl_status', 'gender', 'age']]
couples.head()

	mar_status	empl_status	gender	age
0	1	1	1	51
1	1	1	2	53
2	1	1	1	57
3	1	1	2	57
4	1	1	1	60

Cleaning the dataset

The numbers in the DataFrame correspond to the mappings below.

• 'mar_status': 1=married, 2=unmarried.
• 'empl_status': enumerated in the list below.
• 'gender': 1=male, 2=female.
• 'age': person's age in years.

couples.head()

	mar_status	empl_status	gender	age
0	1	1	1	51
1	1	1	2	53
2	1	1	1	57
3	1	1	2	57
4	1	1	1	60

empl = [
    'Working as paid employee',
    'Working, self-employed',
    'Not working - on a temporary layoff from a job',
    'Not working - looking for work',
    'Not working - retired',
    'Not working - disabled',
    'Not working - other'
]

couples = couples.replace({
    'mar_status': {1: 'married', 2: 'unmarried'},
    'gender': {1: 'M', 2: 'F'},
    'empl_status': {(k + 1): empl[k] for k in range(len(empl))}
})

couples.head()

	mar_status	empl_status	gender	age
0	married	Working as paid employee	M	51
1	married	Working as paid employee	F	53
2	married	Working as paid employee	M	57
3	married	Working as paid employee	F	57
4	married	Working as paid employee	M	60

Understanding the couples dataset

• Who is in our dataset? Mostly young people? Mostly married people? Mostly employed people?
• What is the distribution of values in each column?

# For categorical columns, this shows the 10 most common values and their frequencies.
# For numerical columns, this shows the result of calling the .describe() method.
for col in couples:
    if couples[col].dtype == 'object':
        empr = couples[col].value_counts(normalize=True).to_frame().iloc[:10]
    else:
        empr = couples[col].describe().to_frame()
    display(empr)

	mar_status
married	0.72
unmarried	0.28

	empl_status
Working as paid employee	0.61
Not working - other	0.10
Working, self-employed	0.10
Not working - looking for work	0.07
Not working - disabled	0.06
Not working - retired	0.05
Not working - on a temporary layoff from a job	0.02

	gender
M	0.5
F	0.5

	age
count	2068.00
mean	43.17
std	11.91
...	...
50%	44.00
75%	53.00
max	64.00

8 rows × 1 columns

Let's look at the distribution of age separately for married couples and unmarried couples.

px.histogram(couples, x='age', color='mar_status', histnorm='probability', marginal='box',
             barmode='overlay', opacity=0.7)

How are these two distributions different? Why do you think there is a difference?

Understanding employment status in households

• Do married households more often have a stay-at-home spouse?
• Do households with unmarried couples more often have someone looking for work?
• How much does the employment status of the different households vary?

To answer these questions, let's compute the distribution of employment status conditional on household type (married vs. unmarried).

couples.sample(5).head()

	mar_status	empl_status	gender	age
181	married	Working as paid employee	F	60
1887	unmarried	Working as paid employee	F	27
745	married	Working as paid employee	F	39
1916	unmarried	Working, self-employed	M	36
1241	married	Working as paid employee	F	44

# Note that this is a shortcut to picking a column for values and using aggfunc='count'.
empl_cnts = couples.pivot_table(index='empl_status', columns='mar_status', aggfunc='size')
empl_cnts

mar_status	married	unmarried
empl_status
Not working - disabled	72	45
Not working - looking for work	71	69
Not working - on a temporary layoff from a job	21	13
Not working - other	182	33
Not working - retired	94	11
Working as paid employee	906	347
Working, self-employed	138	66

Since there are a different number of married and unmarried couples in the dataset, we can't compare the numbers above directly. We need to convert counts to proportions, separately for married and unmarried couples.

empl_cnts.sum()

mar_status
married      1484
unmarried     584
dtype: int64

cond_distr = empl_cnts / empl_cnts.sum()
cond_distr

mar_status	married	unmarried
empl_status
Not working - disabled	0.05	0.08
Not working - looking for work	0.05	0.12
Not working - on a temporary layoff from a job	0.01	0.02
Not working - other	0.12	0.06
Not working - retired	0.06	0.02
Working as paid employee	0.61	0.59
Working, self-employed	0.09	0.11

Both of the columns above sum to 1.

Differences in the distributions

Are the distributions of employment status for married people and for unmarried people who live with their partners different?

Is this difference just due to noise?

cond_distr.plot(kind='barh', title='Distribution of Employment Status, Conditional on Household Type', barmode='group')

Permutation test for household composition

• Null Hypothesis: In the US, the distribution of employment status among those who are married is the same as among those who are unmarried and live with their partners. The difference between the two observed samples is due to chance.

• Alternative Hypothesis: In the US, the distributions of employment status of the two groups are different.

Total variation distance

• Whenever we need to compare two categorical distributions, we use the TVD.
  • Recall, the TVD is the sum of the absolute differences in proportions, divided by 2.
• In DSC 10, the only test statistic we ever used in permutation tests was the difference in group means/medians, but the TVD can be used in permutation tests as well.

cond_distr

mar_status	married	unmarried
empl_status
Not working - disabled	0.05	0.08
Not working - looking for work	0.05	0.12
Not working - on a temporary layoff from a job	0.01	0.02
Not working - other	0.12	0.06
Not working - retired	0.06	0.02
Working as paid employee	0.61	0.59
Working, self-employed	0.09	0.11

Let's first compute the observed TVD:

(cond_distr['unmarried'] - cond_distr['married']).abs().sum() / 2

0.1269754089281099

Since we'll need to calculate the TVD repeatedly, let's define a function that computes it.

def tvd_of_groups(df, groups, cats):
    '''groups: the binary column (e.g. married vs. unmarried).
       cats: the categorical column (e.g. employment status).
    '''
    cnts = df.pivot_table(index=cats, columns=groups, aggfunc='size')
    # Normalize each column.
    distr = cnts / cnts.sum()
    # Compute and return the TVD.
    return (distr['unmarried'] - distr['married']).abs().sum() / 2

# Same result as above.
observed_tvd = tvd_of_groups(couples, groups='mar_status', cats='empl_status')
observed_tvd

0.1269754089281099

Simulation

• Under the null hypothesis, marital status is not related to employment status.
• We can shuffle the marital status column and get an equally-likely dataset.
• On each shuffle, we will compute the TVD.
• Once we have many TVDs, we can ask, how often do we see a difference at least as large as our observed difference?

couples.head()

	mar_status	empl_status	gender	age
0	married	Working as paid employee	M	51
1	married	Working as paid employee	F	53
2	married	Working as paid employee	M	57
3	married	Working as paid employee	F	57
4	married	Working as paid employee	M	60

Here, we'll shuffle marital statuses, though remember, we could shuffle employment statuses too.

couples.assign(shuffled_mar=np.random.permutation(couples['mar_status']))

	mar_status	empl_status	gender	age	shuffled_mar
0	married	Working as paid employee	M	51	married
1	married	Working as paid employee	F	53	married
2	married	Working as paid employee	M	57	married
...	...	...	...	...	...
2065	unmarried	Working as paid employee	F	53	married
2066	unmarried	Working as paid employee	M	44	married
2067	unmarried	Working as paid employee	F	42	married

2068 rows × 5 columns

Let's do this repeatedly.

N = 1000
tvds = []

for _ in range(N):
    # Shuffle marital statuses.
    with_shuffled = couples.assign(shuffled_mar=np.random.permutation(couples['mar_status']))
    
    # Compute and store the TVD.
    tvd = tvd_of_groups(with_shuffled, groups='shuffled_mar', cats='empl_status')
    tvds.append(tvd)

Notice that by defining a function that computes our test statistic, our simulation code is much cleaner.

Conclusion of the test

fig = px.histogram(tvds, x=0, nbins=50, histnorm='probability', 
                   title='Empirical Distribution of the TVD')
fig.update_layout(xaxis_range=[0, 0.2])

We reject the null hypothesis that married/unmarried households have similar employment makeups.

We can't say anything about why the employment makeups are different, though!

Summary, next time

Summary

• Both "standard" hypothesis tests and permutation tests are forms of hypothesis tests, which are used to assess whether some observation in our data looks significant.
  • See the end of the "Permutation testing" section for the distinction between the two.
• To run a hypothesis test, we need to choose a test statistic such that large observed values point to one hypothesis and small observed values point to the other. Examples we've seen:
  • Number of heads, absolute difference between number of heads and expected number of heads (coin-flipping example in the pre-lecture reading).
  • Total variation distance.
  • Difference in group means.

Next time

Identifying different ways in which data can be missing. Don't worry, hypothesis testing will be revisited!