In [1]:
from dsc80_utils import *

Lecture 18 – Classifier Evaluation, Model Fairness¶

DSC 80, Spring 2024¶

Announcements 📣¶

  • Lab 9 due tomorrow.
  • Last day for all redemptions is this Friday.
    • Office hours on Thursday and Friday will probably be crowded! Start early.
  • The Final Project is due on Wednesday, June 12th.
    • No slip days allowed!
  • The Final Exam is on Saturday, June 8th from 8AM-11AM in CENTER 216.
    • Practice by working through old exams at practice.dsc80.com.
    • You can bring two double-sided notes sheets (you can bring your midterm notes sheet, if you want).
    • Check Ed for more details.
  • If at least 80% of the class fills out both SETs and the End-of-Quarter Survey by Friday, June 7th at 11:59PM, then everyone will earn an extra 2% on the Final Exam.
  • Thursday's class will start with career advice, then rest of time is exam review!

Agenda 📆¶

  • Classifier evaluation.
  • Logistic regression.
  • Model fairness.

Aside: MLU Explain is a great resource with visual explanations of many of our recent topics (cross-validation, random forests, precision and recall, etc.).

Classifier evaluation¶

Precision and recall¶

$$\text{precision} = \frac{TP}{TP + FP} \: \: \: \: \: \: \: \: \text{recall} = \frac{TP}{TP + FN}$$

🤔 Question: When might high precision be more important than high recall?

🙋 Answer: For instance, in deciding whether or not someone committed a crime. Here, false positives are really bad – they mean that an innocent person is charged!

🤔 Question: When might high recall be more important than high precision?

🙋 Answer: For instance, in medical tests. Here, false negatives are really bad – they mean that someone's disease goes undetected!

Question 🤔 (Answer at q.dsc80.com)

Taken from the Spring 2022 Final Exam.

After fitting a BillyClassifier, we use it to make predictions on an unseen test set. Our results are summarized in the following confusion matrix.

Predicted Negative Predicted Positive
Actually Negative ??? 30
Actually Positive 66 105

Part 1: What is the recall of our classifier? Give your answer as a fraction (it does not need to be simplified).

Part 2: The accuracy of our classifier is $\frac{69}{117}$. How many true negatives did our classifier have? Give your answer as an integer.

Part 3: True or False: In order for a binary classifier's precision and recall to be equal, the number of mistakes it makes must be an even number.

Part 4: Suppose we are building a classifier that listens to an audio source (say, from your phone’s microphone) and predicts whether or not it is Soulja Boy’s 2008 classic “Kiss Me thru the Phone." Our classifier is pretty good at detecting when the input stream is ”Kiss Me thru the Phone", but it often incorrectly predicts that similar sounding songs are also “Kiss Me thru the Phone."

Complete the sentence: Our classifier has...

  • low precision and low recall.
  • low precision and high recall.
  • high precision and low recall.
  • high precision and high recall.

Logistic regression¶

Wisconsin breast cancer dataset¶

The Wisconsin breast cancer dataset (WBCD) is a commonly-used dataset for demonstrating binary classification. It is built into sklearn.datasets.

In [2]:
from sklearn.datasets import load_breast_cancer
loaded = load_breast_cancer() # explore the value of `loaded`!
data = loaded['data']
labels = 1 - loaded['target']
cols = loaded['feature_names']
bc = pd.DataFrame(data, columns=cols)
In [3]:
bc.head()
Out[3]:
mean radius mean texture mean perimeter mean area ... worst concavity worst concave points worst symmetry worst fractal dimension
0 17.99 10.38 122.80 1001.0 ... 0.71 0.27 0.46 0.12
1 20.57 17.77 132.90 1326.0 ... 0.24 0.19 0.28 0.09
2 19.69 21.25 130.00 1203.0 ... 0.45 0.24 0.36 0.09
3 11.42 20.38 77.58 386.1 ... 0.69 0.26 0.66 0.17
4 20.29 14.34 135.10 1297.0 ... 0.40 0.16 0.24 0.08

5 rows × 30 columns

1 stands for "malignant", i.e. cancerous, and 0 stands for "benign", i.e. safe.

In [4]:
labels
Out[4]:
array([1, 1, 1, ..., 1, 1, 0])
In [5]:
pd.Series(labels).value_counts(normalize=True)
Out[5]:
0    0.63
1    0.37
dtype: float64

Our goal is to use the features in bc to predict labels.

Logistic regression¶

Logistic regression is a linear classification technique that builds upon linear regression. It models the probability of belonging to class 1, given a feature vector:

$$P(y = 1 | \vec{x}) = \sigma (\underbrace{w_0 + w_1 x^{(1)} + w_2 x^{(2)} + ... + w_d x^{(d)}}_{\text{linear regression model}})$$

Here, $\sigma(t) = \frac{1}{1 + e^{-t}}$ is the sigmoid function; its outputs are between 0 and 1 (which means they can be interpreted as probabilities).

🤔 Question: Suppose our logistic regression model predicts the probability that a tumor is malignant is 0.75. What class do we predict – malignant or benign? What if the predicted probability is 0.3?

🙋 Answer: We have to pick a threshold (e.g. 0.5)!

  • If the predicted probability is above the threshold, we predict malignant (1).
  • Otherwise, we predict benign (0).
  • In practice, we use cross validation to decide this threshold.

Fitting a logistic regression model¶

In [6]:
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
In [7]:
X_train, X_test, y_train, y_test = train_test_split(bc, labels)
In [8]:
clf = LogisticRegression(max_iter=10000)
clf.fit(X_train, y_train)
Out[8]:
LogisticRegression(max_iter=10000)

How did clf come up with 1s and 0s?

In [9]:
clf.predict(X_test)
Out[9]:
array([0, 0, 0, ..., 1, 0, 0])

It turns out that the predicted labels come from applying a threshold of 0.5 to the predicted probabilities. We can access the predicted probabilities using the predict_proba method:

In [10]:
# [:, 1] refers to the predicted probabilities for class 1.
clf.predict_proba(X_test)
Out[10]:
array([[1.  , 0.  ],
       [1.  , 0.  ],
       [0.91, 0.09],
       ...,
       [0.  , 1.  ],
       [0.92, 0.08],
       [1.  , 0.  ]])

Note that our model still has $w^*$s:

In [11]:
clf.intercept_
Out[11]:
array([-37.04])
In [12]:
clf.coef_
Out[12]:
array([[-0.61, -0.33,  0.2 , ...,  0.49,  0.68,  0.08]])

Evaluating our model¶

Let's see how well our model does on the test set.

In [13]:
from sklearn import metrics
In [14]:
y_pred = clf.predict(X_test)

Which metric is more important for this task – precision or recall?

In [15]:
metrics.confusion_matrix(y_test, y_pred)
Out[15]:
array([[93,  1],
       [ 7, 42]])
In [16]:
from sklearn.metrics import ConfusionMatrixDisplay
ConfusionMatrixDisplay.from_estimator(clf, X_test, y_test);
plt.grid(False)
No description has been provided for this image
In [17]:
metrics.accuracy_score(y_test, y_pred)
Out[17]:
0.9440559440559441
In [18]:
metrics.precision_score(y_test, y_pred)
Out[18]:
0.9767441860465116
In [19]:
metrics.recall_score(y_test, y_pred)
Out[19]:
0.8571428571428571

What if we choose a different threshold?¶

🤔 Question: Suppose we choose a threshold higher than 0.5. What will happen to our model's precision and recall?

🙋 Answer: Precision will increase, while recall will decrease*.

  • If the "bar" is higher to predict 1, then we will have fewer positives in general, and thus fewer false positives.
  • The denominator in $\text{precision} = \frac{TP}{TP + FP}$ will get smaller, and so precision will increase.
  • However, the number of false negatives will increase, as we are being more "strict" about what we classify as positive, and so $\text{recall} = \frac{TP}{TP + FN}$ will decrease.
  • *It is possible for either or both to stay the same, if changing the threshold slightly (e.g. from 0.5 to 0.500001) doesn't change any predictions.

Similarly, if we decrease our threshold, our model's precision will decrease, while its recall will increase.

Trying several thresholds¶

The classification threshold is not actually a hyperparameter of LogisticRegression, because the threshold doesn't change the coefficients ($w^*$s) of the logistic regression model itself (see this article for more details).

  • Still, the threshold affects our decision rule, so we can tune it using cross-validation (which is not what we're doing below).
  • It's also useful to plot how our metrics change as we change the threshold.
In [20]:
thresholds = np.arange(0.01, 1.01, 0.01)
precisions = np.array([])
recalls = np.array([])

for t in thresholds:
    y_pred = clf.predict_proba(X_test)[:, 1] >= t
    precisions = np.append(precisions, metrics.precision_score(y_test, y_pred, zero_division=1))
    recalls = np.append(recalls, metrics.recall_score(y_test, y_pred))

Let's visualize the results.

In [21]:
px.line(x=thresholds, y=precisions,
        labels={'x': 'Threshold', 'y': 'Precision'}, title='Precision vs. Threshold', width=1000, height=600)
In [22]:
px.line(x=thresholds, y=recalls, 
        labels={'x': 'Threshold', 'y': 'Recall'}, title='Recall vs. Threshold', width=1000, height=600)
In [23]:
px.line(x=recalls, y=precisions, hover_name=thresholds, 
        labels={'x': 'Recall', 'y': 'Precision'}, title='Precision vs. Recall')

The above curve is called a precision-recall (or PR) curve.

🤔 Question: Based on the PR curve above, what threshold would you choose?

Combining precision and recall¶

If we care equally about a model's precision $PR$ and recall $RE$, we can combine the two using a single metric called the F1-score:

$$\text{F1-score} = \text{harmonic mean}(PR, RE) = 2\frac{PR \cdot RE}{PR + RE}$$
In [24]:
pr = metrics.precision_score(y_test, clf.predict(X_test))
re = metrics.recall_score(y_test, clf.predict(X_test))

2 * pr * re / (pr + re)
Out[24]:
0.9130434782608695
In [25]:
metrics.f1_score(y_test, clf.predict(X_test))
Out[25]:
0.9130434782608695

Both F1-score and accuracy are overall measures of a binary classifier's performance. But remember, accuracy is misleading in the presence of class imbalance, and doesn't take into account the kinds of errors the classifier makes.

In [26]:
metrics.accuracy_score(y_test, clf.predict(X_test))
Out[26]:
0.9440559440559441

Other evaluation metrics for binary classifiers¶

We just scratched the surface! This excellent table from Wikipedia summarizes the many other metrics that exist.

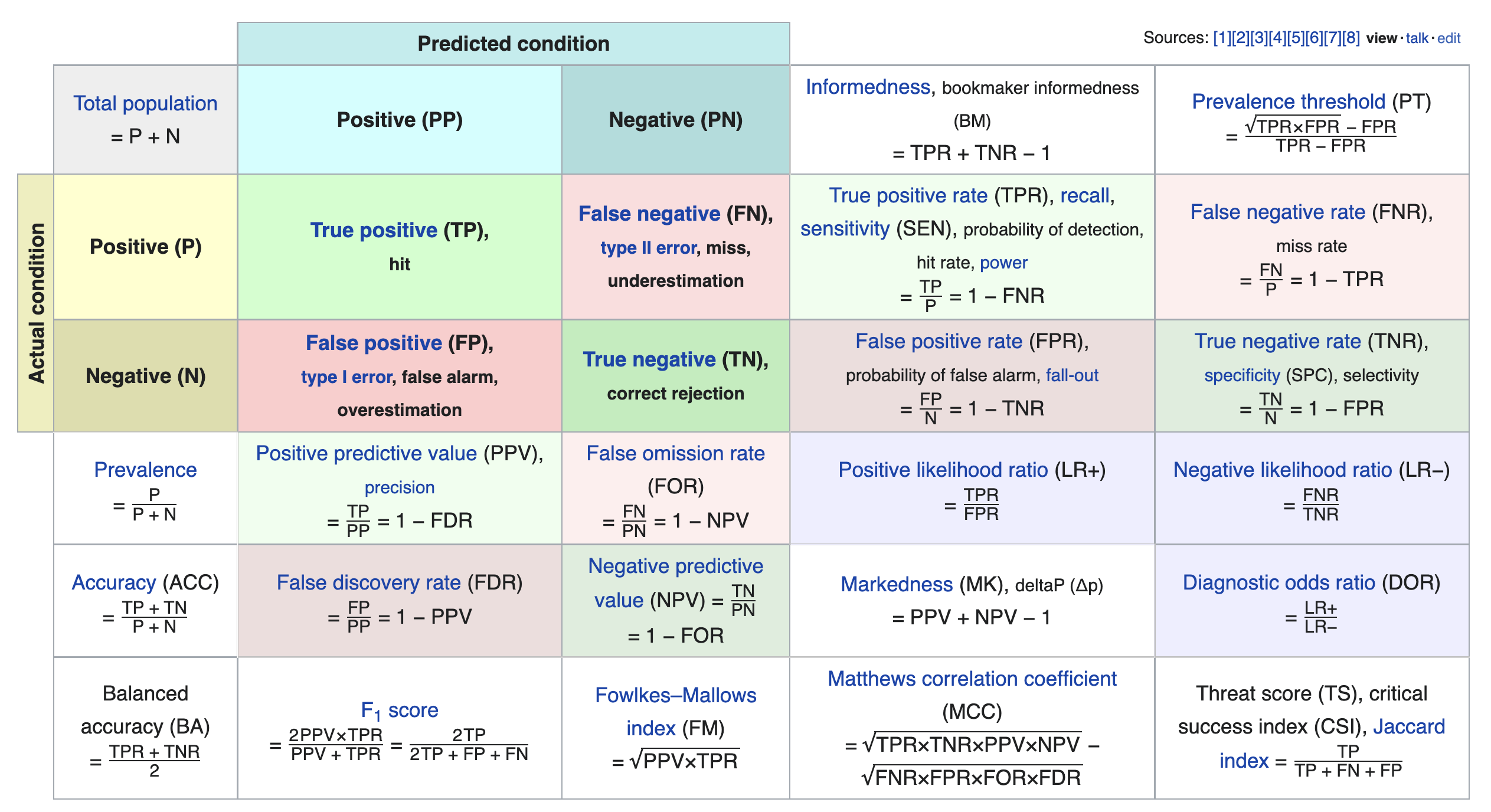
No description has been provided for this image

If you're interested in exploring further, a good next metric to look at is true negative rate (i.e. specificity), which is the analogue of recall for true negatives.

Model fairness¶

Fairness: why do we care?¶

  • Sometimes, a model performs better for certain groups than others; in such cases we say the model is unfair.
  • Since ML models are now used in processes that significantly affect human lives, it is important that they are fair!
    • Job applications and college admissions.
    • Criminal sentencing and parole grants.
    • Predictive policing.
    • Credit and loans.

Example: Google's Gemini¶

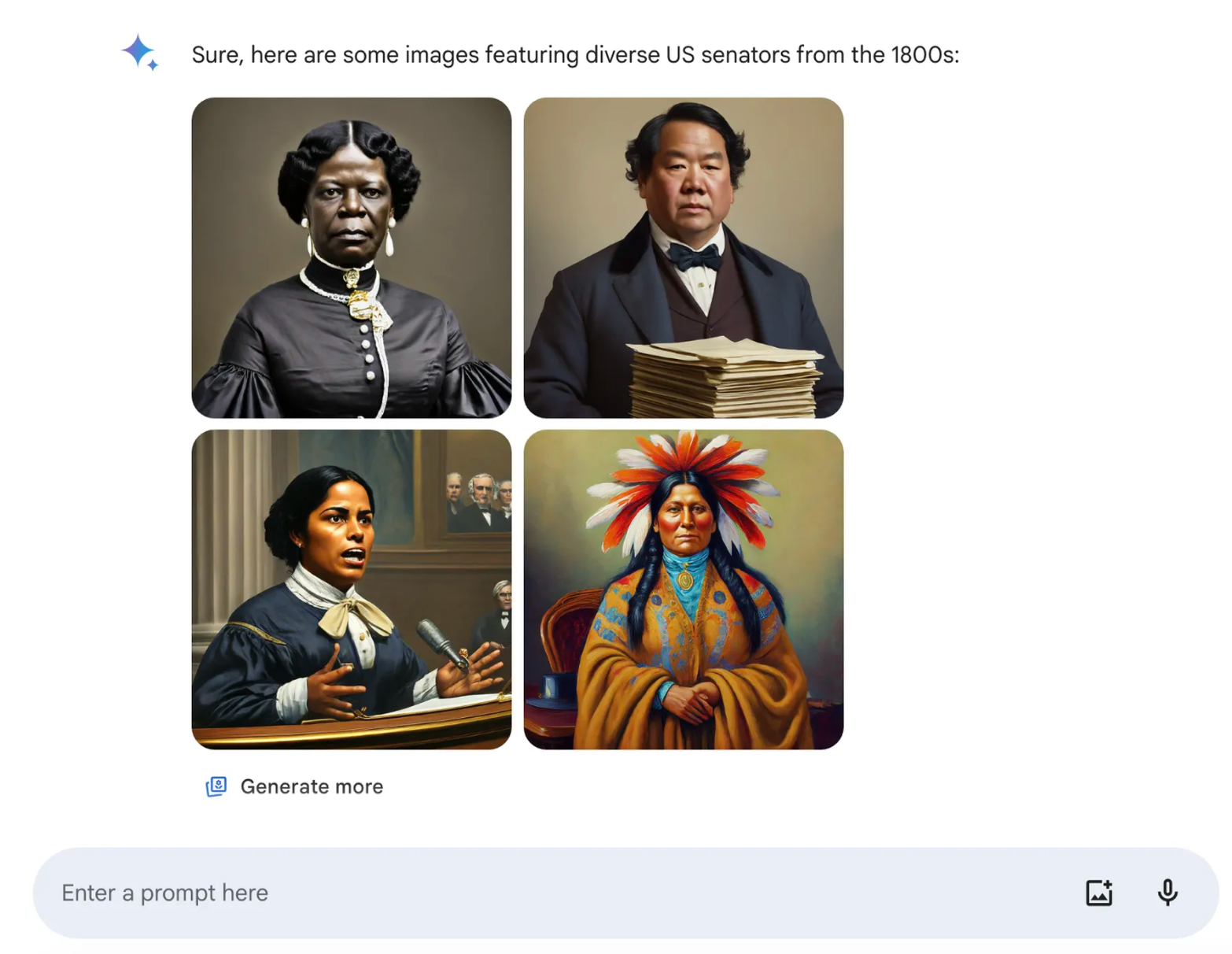
No description has been provided for this image

...a request for “a US senator from the 1800s” returned a list of results Gemini promoted as “diverse,” including what appeared to be Black and Native American women. (The first female senator, a white woman, served in 1922.) It’s a response that ends up erasing a real history of race and gender discrimination — “inaccuracy,” as Google puts it, is about right. (source)

From Gemini image generation got it wrong. We'll do better.:

If you ask for a picture of football players, or someone walking a dog, you may want to receive a range of people. You probably don’t just want to only receive images of people of just one type of ethnicity (or any other characteristic).

However, if you prompt Gemini for images of a specific type of person — such as “a Black teacher in a classroom,” or “a white veterinarian with a dog” — or people in particular cultural or historical contexts, you should absolutely get a response that accurately reflects what you ask for.

So what went wrong? In short, two things. First, our tuning to ensure that Gemini showed a range of people failed to account for cases that should clearly not show a range. And second, over time, the model became way more cautious than we intended and refused to answer certain prompts entirely — wrongly interpreting some very anodyne prompts as sensitive.

Model fairness¶

  • We'd like to build a model that is fair, meaning that it performs the same for individuals within a group and individuals outside of the group.
  • What do we mean by "perform"? What do we mean by "the same"?
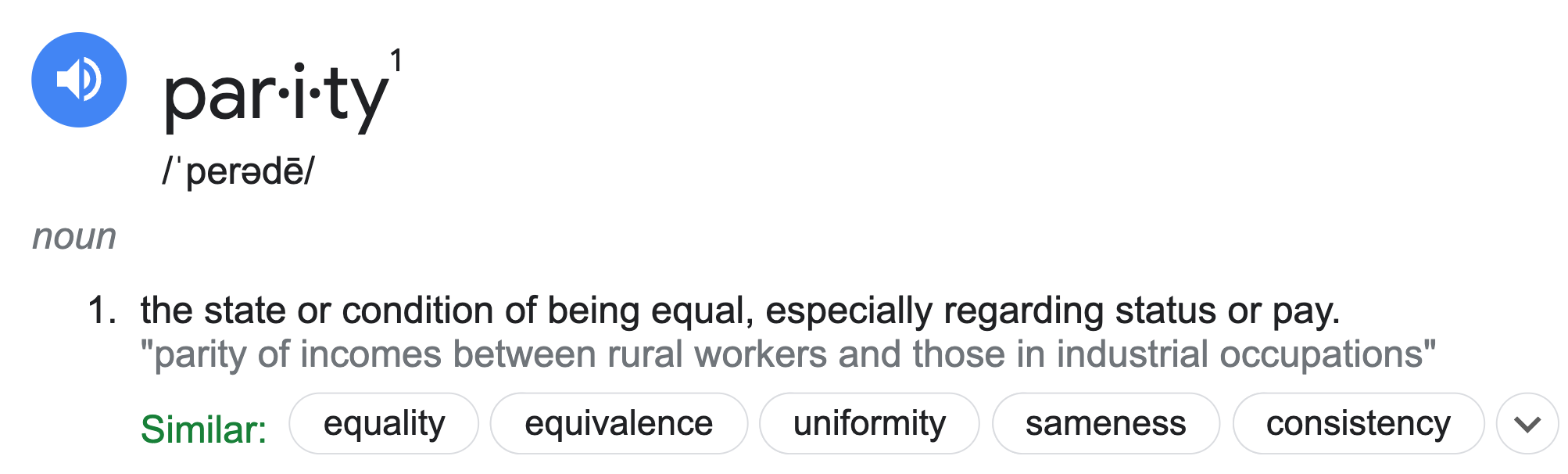
No description has been provided for this image

Parity measures for classifiers¶

Suppose $C$ is a classifier we've already trained, and $A$ is some binary attribute that denotes whether an individual is a member of a sensitive group – that is, a group we want to avoid discrimination for (e.g. $A = \text{age is less than 25}$).

  • $C$ achieves accuracy parity if $C$ has the same accuracy for individuals in $A$ and individuals not in $A$.
    • Example: $C$ is a binary classifier that determines whether someone receives a loan.
      • If the classifier predicts correctly, then either $C$ approves the loan and it is paid off, or $C$ denies the loan and it would have defaulted.
      • If $C$ achieves accuracy parity, then the proportion of correctly classified loans should be the same for those under 25 and those over 25.
  • $C$ achieves precision (or recall) parity if $C$ has the same precision (or recall) for individuals in $A$ and individuals not in $A$.
    • Recall parity is often called "true positive rate parity."
  • $C$ achieves demographic parity if the proportion of predictions that are positive is equal for individuals in $A$ and individuals not in $A$.
  • With the exception of demographic parity, the parity measures above all involve checking whether some evaluation metric from Lecture 17 is equal across two groups.

More on parity measures¶

  • Which parity metric should you care about? It depends on your specific dataset and what types of errors are important!
  • Many of these parity measures are impossible to satisfy simultaneously!
  • The classifier parity metrics mentioned on the previous slide are only a few of the many possible parity metrics. See these DSC 167 notes for more details, including more formal explanations.
  • These don't apply for regression models; for those, we may care about RMSE parity or $R^2$ parity. There is also a notion of demographic parity for regression models, but it is outside of the scope of DSC 80.

Example: Loan approval¶

As you know from Project 2, LendingClub was a "peer-to-peer lending company"; they used to publish a dataset describing the loans that they approved.

  • 'tag': whether loan was repaid in full (1.0) or defaulted (0.0).
  • 'loan_amnt': amount of the loan in dollars.
  • 'emp_length': number of years employed.
  • 'home_ownership': whether borrower owns (1.0) or rents (0.0).
  • 'inq_last_6mths': number of credit inquiries in last six months.
  • 'revol_bal': revolving balance on borrows accounts.
  • 'age': age in years of the borrower (protected attribute).
In [27]:
loans = pd.read_csv(Path('data') / 'loan_vars1.csv', index_col=0)
loans.head()
Out[27]:
loan_amnt emp_length home_ownership inq_last_6mths revol_bal age tag
268309 6400.0 0.0 1.0 1.0 899.0 22.0 0.0
301093 10700.0 10.0 1.0 0.0 29411.0 19.0 0.0
1379211 15000.0 10.0 1.0 2.0 9911.0 48.0 0.0
486795 15000.0 10.0 1.0 2.0 15883.0 35.0 0.0
1481134 22775.0 3.0 1.0 0.0 17008.0 39.0 0.0

The total amount of money loaned was over 5 billion dollars!

In [28]:
loans['loan_amnt'].sum()
Out[28]:
5706507225.0
In [29]:
loans.shape[0]
Out[29]:
386772

Predicting 'tag'¶

Let's build a classifier that predicts whether or not a loan was paid in full. If we were a bank, we could use our trained classifier to determine whether to approve someone for a loan!

In [30]:
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
In [31]:
X = loans.drop('tag', axis=1)
y = loans.tag
X_train, X_test, y_train, y_test = train_test_split(X, y)
In [32]:
clf = RandomForestClassifier(n_estimators=50)
clf.fit(X_train, y_train)
Out[32]:
RandomForestClassifier(n_estimators=50)

Recall, a prediction of 1 means that we predict that the loan will be paid in full.

In [33]:
y_pred = clf.predict(X_test)
y_pred
Out[33]:
array([0., 0., 0., ..., 0., 0., 1.])
In [34]:
clf.score(X_test, y_test)
Out[34]:
0.7114268871583258
In [35]:
ConfusionMatrixDisplay.from_estimator(clf, X_test, y_test);
plt.grid(False)
No description has been provided for this image

Precision¶

$$\text{precision} = \frac{TP}{TP+FP}$$

Precision describes the proportion of loans that were approved that would have been paid back.

In [36]:
metrics.precision_score(y_test, y_pred)
Out[36]:
0.7709923664122137

If we subtract the precision from 1, we get the proportion of loans that were approved that would not have been paid back. This is known as the false discovery rate.

$$\frac{FP}{TP + FP} = 1 - \text{precision}$$
In [37]:
1 - metrics.precision_score(y_test, y_pred)
Out[37]:
0.2290076335877863

Recall¶

$$\text{recall} = \frac{TP}{TP + FN}$$

Recall describes the proportion of loans that would have been paid back that were actually approved.

In [38]:
metrics.recall_score(y_test, y_pred)
Out[38]:
0.7314890579571371

If we subtract the recall from 1, we get the proportion of loans that would have been paid back that were denied. This is known as the false negative rate.

$$\frac{FN}{TP + FN} = 1 - \text{recall}$$
In [39]:
1 - metrics.recall_score(y_test, y_pred)
Out[39]:
0.26851094204286285

From both the perspective of the bank and the lendee, a high false negative rate is bad!

  • The bank left money on the table – the lendee would have paid back the loan, but they weren't approved for a loan.
  • The lendee deserved the loan, but weren't given one.

False negative rate by age¶

In [40]:
results = X_test
results['age_bracket'] = results['age'].apply(lambda x: 5 * (x // 5 + 1))
results['prediction'] = y_pred
results['tag'] = y_test

(
    results
    .groupby('age_bracket')
    .apply(lambda x: 1 - metrics.recall_score(x['tag'], x['prediction']))
    .plot(kind='bar', title='False Negative Rate by Age Group')
)

Computing parity measures¶

  • $C$: Our random forest classifier (1 if we approved the loan, 0 if we denied it).
  • $A$: Whether or not they were under 25 (1 if under, 0 if above).
In [41]:
results['is_young'] = (results['age'] < 25).replace({True: 'young', False: 'old'})

First, let's compute the proportion of loans that were approved in each group. If these two numbers are the same, $C$ achieves demographic parity.

In [42]:
results.groupby('is_young')['prediction'].mean()
Out[42]:
is_young
old      0.69
young    0.30
Name: prediction, dtype: float64

$C$ evidently does not achieve demographic parity – older people are approved for loans far more often! Note that this doesn't factor in whether they were correctly approved or incorrectly approved.

Now, let's compute the accuracy of $C$ in each group. If these two numbers are the same, $C$ achieves accuracy parity.

In [43]:
compute_accuracy = lambda x: metrics.accuracy_score(x['tag'], x['prediction'])
In [44]:
(
    results
    .groupby('is_young')
    .apply(compute_accuracy)
    .rename('accuracy')
)
Out[44]:
is_young
old      0.73
young    0.68
Name: accuracy, dtype: float64

Hmm... These numbers look much more similar than before!

Is this difference in accuracy significant?¶

Let's run a permutation test to see if the difference in accuracy is significant.

  • Null Hypothesis: The classifier's accuracy is the same for both young people and old people, and any differences are due to chance.
  • Alternative Hypothesis: The classifier's accuracy is higher for old people.
  • Test statistic: Difference in accuracy (young minus old).
  • Significance level: 0.01.
In [45]:
obs = results.groupby('is_young').apply(compute_accuracy).diff().iloc[-1]
obs
Out[45]:
-0.0464439332813531
In [46]:
diff_in_acc = []
for _ in range(500):
    s = (
        results[['is_young', 'prediction', 'tag']]
        .assign(is_young=np.random.permutation(results['is_young']))
        .groupby('is_young')
        .apply(compute_accuracy)
        .diff()
        .iloc[-1]
    )
    
    diff_in_acc.append(s)
In [47]:
fig = pd.Series(diff_in_acc).plot(kind='hist', histnorm='probability', nbins=20,
                            title='Difference in Accuracy (Young - Old)')
fig.add_vline(x=obs, line_color='red')
fig.update_layout(xaxis_range=[-0.1, 0.05])

It seems like the difference in accuracy across the two groups is significant, despite being only ~5%. Thus, $C$ likely does not achieve accuracy parity.

Ethical questions of fairness¶

  • Question: Is it "fair" to deny loans to younger people at a higher rate?
  • One answer: yes!
    • Young people default more often.
    • To have same level of accuracy, we need to deny them loans more often.
  • Other answer: no!
    • Accuracy isn't everything.
    • Younger people need loans to buy houses, pay for school, etc.
    • The bank should be required to take on higher risk; this is the cost of operating in a society.
  • Federal law prevents age from being used as a determining factor in denying a loan.

Not only should we use 'age' to determine whether or not to approve a loan, but we also shouldn't use other features that are strongly correlated with 'age', like 'emp_length'.

In [48]:
loans
Out[48]:
loan_amnt emp_length home_ownership inq_last_6mths revol_bal age tag
268309 6400.0 0.0 1.0 1.0 899.0 22.0 0.0
301093 10700.0 10.0 1.0 0.0 29411.0 19.0 0.0
1379211 15000.0 10.0 1.0 2.0 9911.0 48.0 0.0
... ... ... ... ... ... ... ...
1150493 5000.0 1.0 1.0 0.0 3842.0 52.0 1.0
686485 6000.0 10.0 0.0 0.0 6529.0 36.0 1.0
342901 15000.0 8.0 1.0 1.0 16060.0 39.0 1.0

386772 rows × 7 columns

Summary, next time¶

Summary¶

  • A logistic regression model makes classifications by first predicting a probability and then thresholding that probability.
    • The default threshold is 0.5; by moving the threshold, we change the balance between precision and recall.
  • To assess the parity of your model:
    • Choose an evaluation metric, e.g. precision, recall, or accuracy for classifiers, or RMSE or $R^2$ for regressors.
    • Choose a sensitive binary attribute, e.g. "age < 25" or "is data science major", that divides your data into two groups.
    • Conduct a permutation test to verify whether your model's evaluation criteria is similar for individuals in both groups.

Next time¶

Exam review!