In [1]:
from dsc80_utils import *
In [2]:
# The dataset is built into plotly (and seaborn)!
# We shuffle here so that the head of the DataFrame contains rows where smoker is Yes and smoker is No,
# purely for illustration purposes (it doesn't change any of the math).
np.random.seed(1)
tips = px.data.tips().sample(frac=1).reset_index(drop=True)

Lecture 14 – Feature Engineering¶

DSC 80, Summer 2024¶

Announcements 📣¶

  • Lab 7 is due tomorrow.
  • The Final Project is out!
    • It will be worth two projects (because it used to be two separate projects).
    • You cannot request an extension on final submission deadline on Saturday, August 8.

Agenda 📆¶

  • Review: Predicting tips.
    • $R^2$.
  • Feature engineering.
    • Example: Predicting tips.
      • One hot encoding.
    • Example: Predicting ratings ⭐️.
      • Dropping features.
      • Ordinal encoding.
    • Example: Horsepower 🚗.
      • Quantitative scaling.
  • Feature engineering in sklearn.
    • Transformer classes.
    • Creating Pipelines.

Review: Predicting tips 🧑‍🍳¶

In [3]:
tips
Out[3]:
total_bill tip sex smoker day time size
0 3.07 1.00 Female Yes Sat Dinner 1
1 18.78 3.00 Female No Thur Dinner 2
2 26.59 3.41 Male Yes Sat Dinner 3
... ... ... ... ... ... ... ...
241 17.47 3.50 Female No Thur Lunch 2
242 10.07 1.25 Male No Sat Dinner 2
243 16.93 3.07 Female No Sat Dinner 3

244 rows × 7 columns

Linear models¶

Last time, we fit three linear models to predict restaurant tips:

  • Constant model: $\text{predicted tip} = h$.
  • Simple linear regression: $\text{predicted tip} = w_0 + w_1 \cdot \text{total bill}$.
  • Multiple linear regression: $\text{predicted tip} = w_0 + w_1 \cdot \text{total bill} + w_2 \cdot \text{table size}$.

In the constant model case, we know that the optimal model parameter, when using squared loss, is $h^* = \text{mean tip}$.

In [5]:
mean_tip = tips['tip'].mean()

In the other two cases, we used the LinearRegression class from sklearn to help us find optimal model parameters.

In [7]:
from sklearn.linear_model import LinearRegression

model = LinearRegression()
model.fit(X=tips[['total_bill']], y=tips['tip'])

model_two = LinearRegression()
model_two.fit(X=tips[['total_bill', 'size']], y=tips['tip'])
Out[7]:
LinearRegression()

Root mean squared error¶

To compare the performance of different models, we used the root mean squared error (RMSE).

$$\text{RMSE} = \sqrt{\frac{1}{n} \sum_{i = 1}^n \big( y_i - H(x_i) \big)^2}$$

In [8]:
def rmse(actual, pred):
    return np.sqrt(np.mean((actual - pred) ** 2))

rmse_dict = {}
rmse_dict['constant tip amount'] = rmse(tips['tip'], mean_tip)

all_preds = model.predict(tips[['total_bill']])
rmse_dict['one feature: total bill'] = rmse(tips['tip'], all_preds)

rmse_dict['two features'] = rmse(
    tips['tip'], model_two.predict(tips[['total_bill', 'size']])
)

pd.DataFrame({'rmse': rmse_dict.values()}, index=rmse_dict.keys())
Out[8]:
rmse
constant tip amount 1.38
one feature: total bill 1.02
two features 1.01

The .score method of a LinearRegression object¶

Model objects in sklearn that have already been fit have a score method.

In [9]:
model_two.score(tips[['total_bill', 'size']], tips['tip'])
Out[9]:
0.46786930879612565

That doesn't look like the RMSE... what is it? 🤔

Aside: $R^2$¶

  • $R^2$, or the coefficient of determination, is a measure of the quality of a linear fit.
  • There are a few equivalent ways of computing it, assuming your model is linear and has an intercept term:

$$R^2 = \frac{\text{var}(\text{predicted $y$ values})}{\text{var}(\text{actual $y$ values})}$$

$$R^2 = \left[ \text{correlation}(\text{predicted $y$ values}, \text{actual $y$ values}) \right]^2$$

  • Interpretation: $R^2$ is the proportion of variance in $y$ that the linear model explains.
  • In the simple linear regression case, it is the square of the correlation coefficient, $r$.
  • Key idea: $R^2$ ranges from 0 to 1. The closer it is to 1, the better the linear fit is.
    • $R^2$ has no units of measurement, unlike RMSE.

Calculating $R^2$¶

Let's calculate the $R^2$ for model_two's predictions in three different ways.

In [10]:
pred = tips.assign(predicted=model_two.predict(tips[['total_bill', 'size']]))
pred
Out[10]:
total_bill tip sex smoker day time size predicted
0 3.07 1.00 Female Yes Sat Dinner 1 1.15
1 18.78 3.00 Female No Thur Dinner 2 2.80
2 26.59 3.41 Male Yes Sat Dinner 3 3.71
... ... ... ... ... ... ... ... ...
241 17.47 3.50 Female No Thur Lunch 2 2.67
242 10.07 1.25 Male No Sat Dinner 2 1.99
243 16.93 3.07 Female No Sat Dinner 3 2.82

244 rows × 8 columns

Method 1: $R^2 = \frac{\text{var}(\text{predicted $y$ values})}{\text{var}(\text{actual $y$ values})}$

In [11]:
np.var(pred['predicted']) / np.var(pred['tip'])
Out[11]:
0.46786930879612615

Method 2: $R^2 = \left[ \text{correlation}(\text{predicted $y$ values}, \text{actual $y$ values}) \right]^2$

Note: By correlation here, we are referring to $r$, the same correlation coefficient you saw in DSC 10.

In [10]:
pred.corr().loc['predicted', 'tip'] ** 2
Out[10]:
0.46786930879612554

Method 3: LinearRegression.score

In [11]:
model_two.score(tips[['total_bill', 'size']], tips['tip'])
Out[11]:
0.46786930879612565

All three methods provide the same result!

Relationship between $R^2$ and RMSE¶

For linear models with an intercept term,

$$R^2 = 1 - \frac{\text{RMSE}^2}{\text{var}(\text{actual $y$ values})}$$

In [12]:
1 - rmse(pred['tip'], pred['predicted']) ** 2 / np.var(pred['tip'])
Out[12]:
0.46786930879612554

What's next?¶

In [13]:
tips.head()
Out[13]:
total_bill tip sex smoker day time size
0 3.07 1.00 Female Yes Sat Dinner 1
1 18.78 3.00 Female No Thur Dinner 2
2 26.59 3.41 Male Yes Sat Dinner 3
3 14.26 2.50 Male No Thur Lunch 2
4 21.16 3.00 Male No Thur Lunch 2

  • So far, in our journey to predict 'tip', we've only used the existing numerical features in our dataset, 'total_bill' and 'size'.

  • There's a lot of information in tips that we didn't use – 'sex', 'smoker', 'day', and 'time', for example. We can't use these features in their current form, because they're non-numeric.

  • How do we use categorical features in a regression model?

Feature engineering ⚙️¶

The goal of feature engineering¶

  • Feature engineering is the act of finding transformations that transform data into effective quantitative variables.
  • A feature function $\phi$ (phi, pronounced "fea") is a mapping from raw data to $d$-dimensional space, i.e. $\phi: \text{raw data} \rightarrow \mathbb{R}^d$.
    • If two observations $x_i$ and $x_j$ are "similar" in the raw data space, then $\phi(x_i)$ and $\phi(x_j)$ should also be "similar."
  • A "good" choice of features depends on many factors:
    • The kind of data, i.e. quantitative, ordinal, or nominal.
    • The relationship(s) being modeled.
    • The model type, e.g. linear models, decision tree models, neural networks.
  • To introduce different feature functions, we'll look at several different example datasets.

One hot encoding¶

  • One hot encoding is a transformation that turns a categorical feature into several binary features.
  • Suppose a column has $N$ unique values, $A_1$, $A_2$, ..., $A_N$. For each unique value $A_i$, we define the following feature function:

$$\phi_i(x) = \left\{\begin{array}{ll}1 & {\rm if\ } x = A_i \\ 0 & {\rm if\ } x\neq A_i \\ \end{array}\right. $$

  • Note that 1 means "yes" and 0 means "no".
  • One hot encoding is also called "dummy encoding", and $\phi(x)$ may also be referred to as an "indicator variable".

Example: One hot encoding 'smoker'¶

For each unique value of 'smoker' in our dataset, we must create a column for just that 'smoker'. (Remember, 'smoker' is 'Yes' when the table was in the smoking section of the restaurant and 'No' otherwise.)

In [14]:
tips.head()
Out[14]:
total_bill tip sex smoker day time size
0 3.07 1.00 Female Yes Sat Dinner 1
1 18.78 3.00 Female No Thur Dinner 2
2 26.59 3.41 Male Yes Sat Dinner 3
3 14.26 2.50 Male No Thur Lunch 2
4 21.16 3.00 Male No Thur Lunch 2
In [15]:
tips['smoker'].value_counts()
Out[15]:
No     151
Yes     93
Name: smoker, dtype: int64
In [15]:
(tips['smoker'] == 'Yes').astype(int).head()
Out[15]:
0    1
1    0
2    1
3    0
4    0
Name: smoker, dtype: int64
In [16]:
for val in tips['smoker'].unique():
    tips[f'smoker == {val}'] = (tips['smoker'] == val).astype(int)
In [17]:
tips.head()
Out[17]:
total_bill tip sex smoker ... time size smoker == Yes smoker == No
0 3.07 1.00 Female Yes ... Dinner 1 1 0
1 18.78 3.00 Female No ... Dinner 2 0 1
2 26.59 3.41 Male Yes ... Dinner 3 1 0
3 14.26 2.50 Male No ... Lunch 2 0 1
4 21.16 3.00 Male No ... Lunch 2 0 1

5 rows × 9 columns

Model #4: Multiple linear regression using total bill, table size, and smoker status¶

Now that we've converted 'smoker' to a numerical variable, we can use it as input in a regression model. Here's the model we'll try to fit:

$$\text{predicted tip} = w_0 + w_1 \cdot \text{total bill} + w_2 \cdot \text{table size} + w_3 \cdot \text{smoker == Yes}$$

Subtlety: There's no need to use both 'smoker == No' and 'smoker == Yes'. If we know the value of one, we already know the value of the other. We can use either one.

In [18]:
model_three = LinearRegression()
model_three.fit(tips[['total_bill', 'size', 'smoker == Yes']], tips['tip'])
Out[18]:
LinearRegression()

The following cell gives us our $w^*$s:

In [20]:
model_three.intercept_, model_three.coef_
Out[20]:
(0.7090155167346053, array([ 0.09,  0.18, -0.08]))

Thus, our trained linear model to predict tips given total bills, table sizes, and smoker status (yes or no) is:

$$\text{predicted tip} = 0.709 + 0.094 \cdot \text{total bill} + 0.180 \cdot \text{table size} - 0.083 \cdot \text{smoker == Yes}$$

Visualizing Model #4¶

Our new fit model is:

$$\text{predicted tip} = 0.709 + 0.094 \cdot \text{total bill} + 0.180 \cdot \text{table size} - 0.083 \cdot \text{smoker == Yes}$$

To visualize our data and linear model, we'd need 4 dimensions:

  • One for total bill
  • One for table size
  • One for 'smoker == Yes'.
  • One for tip.

Humans can't visualize in 4D, but there may be a solution. We know that 'smoker == Yes' only has two possible values, 1 or 0, so let's look at those cases separately.

Case 1: 'smoker == Yes' is 1, meaning that the table was in the smoking section.

$$\begin{align*} \text{predicted tip} &= 0.709 + 0.094 \cdot \text{total bill} + 0.180 \cdot \text{table size} - 0.083 \cdot 1 \\ &= 0.626 + 0.094 \cdot \text{total bill} + 0.180 \cdot \text{table size} \end{align*}$$

Case 2: 'smoker == Yes' is 0, meaning that the table was not in the smoking section.

$$\begin{align*} \text{predicted tip} &= 0.709 + 0.094 \cdot \text{total bill} + 0.180 \cdot \text{table size} - 0.083 \cdot 0 \\ &= 0.709 + 0.094 \cdot \text{total bill} + 0.180 \cdot \text{table size} \end{align*}$$

Key idea: These are two parallel planes in 3D, with different $z$-intercepts!

Note that the two planes are very close to one another – you'll have to zoom in to see the difference.

In [19]:
# pio.renderers.default = 'plotly_mimetype+notebook' # If it doesn't render, try uncommenting this.

XX, YY = np.mgrid[0:50:2, 0:8:1]
Z_0 = model_three.intercept_ + model_three.coef_[0] * XX + model_three.coef_[1] * YY + model_three.coef_[2] * 0
Z_1 = model_three.intercept_ + model_three.coef_[0] * XX + model_three.coef_[1] * YY + model_three.coef_[2] * 1
plane_0 = go.Surface(x=XX, y=YY, z=Z_0, colorscale='Greens')
plane_1 = go.Surface(x=XX, y=YY, z=Z_1, colorscale='Purples')

fig = go.Figure(data=[plane_0, plane_1])

tips_0 = tips[tips['smoker'] == 'No']
tips_1 = tips[tips['smoker'] == 'Yes']

fig.add_trace(go.Scatter3d(x=tips_0['total_bill'], 
                           y=tips_0['size'], 
                           z=tips_0['tip'], mode='markers', marker = {'color': 'green'}))

fig.add_trace(go.Scatter3d(x=tips_1['total_bill'], 
                           y=tips_1['size'], 
                           z=tips_1['tip'], mode='markers', marker = {'color': 'purple'}))

fig.update_layout(scene = dict(
    xaxis_title='Total Bill',
    yaxis_title='Table Size',
    zaxis_title='Tip'),
  title='Tip vs. Total Bill and Table Size (Green = Non-Smoking Section, Purple = Smoking Section)',
    width=1000, height=800,
    showlegend=False)

If we want to visualize in 2D, we need to pick a single feature to place on the $x$-axis.

In [20]:
fig = go.Figure()
fig.add_trace(go.Scatter(x=tips['total_bill'], y=tips['tip'], 
                         mode='markers', name='Original Data'))
fig.add_trace(go.Scatter(x=tips['total_bill'], y=model_three.predict(tips[['total_bill', 'size', 'smoker == Yes']]), 
                         mode='markers', name='Predicted Tips using Total Bill, <br>Table Size, and Smoker Status'))

fig.update_layout(showlegend=True, title='Tip vs. Total Bill',
                  xaxis_title='Total Bill', yaxis_title='Tip')

Despite being a linear model, why doesn't this model look like a straight line?

Comparing Model #4 to earlier models¶

In [21]:
rmse_dict['three features'] = rmse(tips['tip'], 
                                   model_three.predict(tips[['total_bill', 'size', 'smoker == Yes']]))
rmse_dict
Out[21]:
{'constant tip amount': 1.3807999538298952,
 'one feature: total bill': 1.0178504025697377,
 'two features': 1.007256127114662,
 'three features': 1.0064899786822128}

Adding 'smoker == Yes' decreased the training RMSE of our model, but barely.

Reflection¶

In [24]:
tips.head()
Out[24]:
total_bill tip sex smoker ... time size smoker == Yes smoker == No
0 3.07 1.00 Female Yes ... Dinner 1 1 0
1 18.78 3.00 Female No ... Dinner 2 0 1
2 26.59 3.41 Male Yes ... Dinner 3 1 0
3 14.26 2.50 Male No ... Lunch 2 0 1
4 21.16 3.00 Male No ... Lunch 2 0 1

5 rows × 9 columns

  • We've one hot encoded 'smoker', but it required a for-loop.

  • Is there an easy way to one hot encode all four categorical columns – 'sex', 'smoker', 'day', and 'time' – all at once, without using a for-loop?

  • Yes, using sklearn.preprocessing's OneHotEncoder. More on this soon!

Question 🤔 (Answer at q.dsc80.com)

(Fa23 Final Q9.1)

Every week, Lauren goes to her local grocery store and buys a varying amount of vegetable but always buys exactly one pound of meat (either beef, fish, or chicken). We use a linear regression model to predict her total grocery bill. We’ve collected a dataset containing the pounds of vegetables bought, the type of meat bought, and the total bill. Below we display the first few rows of the dataset and two plots generated using the entire training set.

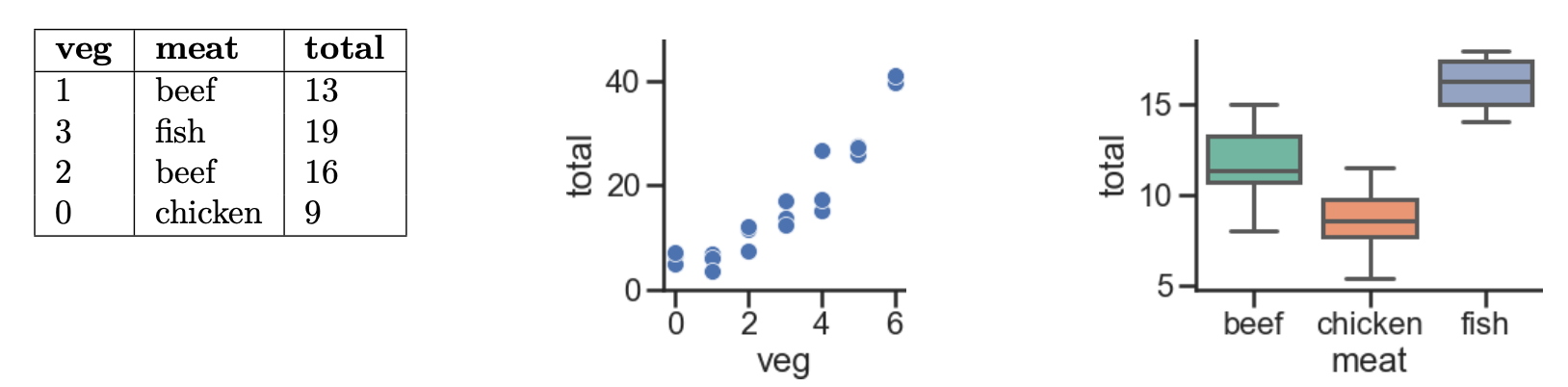
Suppose we fit the following linear regression models to predict total. Based on the data and visualizations shown above, determine whether the fitted model weights are positive (+), negative (-), or exactly 0. The notation meat=beef refers to the one-hot encoded meat column with value 1 if the original value in the meat column was beef and 0 otherwise. Likewise, meat=chicken and meat=fish are the one-hot encoded meat columns for chicken and fish, respectively.

  1. $H(x) = w_0 $
  2. $H(x) = w_0 + w_1 \cdot \text{veg} $
  3. $H(x) = w_0 + w_1 \cdot (\text{meat=chicken}) $
  4. $H(x) = w_0 + w_1 \cdot (\text{meat=beef}) + w_2 \cdot (\text{meat=chicken}) $
  5. $H(x) = w_0 + w_1 \cdot (\text{meat=beef}) + w_2 \cdot (\text{meat=chicken}) + w_3 \cdot (\text{meat=fish}) $

Example: Predicting ratings ⭐️¶

Example: Predicting ratings ⭐️¶

UID AGE STATE HAS_BOUGHT REVIEW | RATING
74 32 NY True "Meh." | ✩✩
42 50 WA True "Worked out of the box..." | ✩✩✩✩
57 16 CA NULL "Sick af..." | ✩
... ... ... ... ... | ...
(int) (int) (str) (bool) (str) | (str)
  • We want to build a classifier that predicts 'RATING' using the above features.
  • Why can't we build a model right away? What must we do so that we can build a model?
  • Some issues: missing values, emojis and strings instead of numbers, irrelevant columns.

Uninformative features¶

  • 'UID' was likely used to join the user information (e.g., 'AGE' and 'STATE') with some reviews dataset.
  • Even though 'UID's are stored as numbers, the numerical value of a user's 'UID' won't help us predict their 'RATING'.
  • If we include the 'UID' feature, our model will find whatever patterns it can between 'UID's and 'RATING's in the training (observed data).
    • This will lead to a lower training RMSE.
  • However, since there is truly no relationship between 'UID' and 'RATING', this will lead to worse model performance on unseen data (bad).

Dropping features¶

There are certain scenarios where manually dropping features might be helpful:

  1. When the features do not contain information associated with the prediction task.
  2. When the feature is not available at prediction time.
  • The goal of building a model to predict 'RATING's is so that we can predict 'RATING's for users who haven't actually made a 'RATING' yet.
  • As such, our model should only depend on features that we would know before the user makes their 'RATING'.
  • For instance, if a user only enters a 'REVIEW' after entering a 'RATING', we shouldn't use their 'REVIEW' to predict their 'RATING'.

Encoding ordinal features¶

UID AGE STATE HAS_BOUGHT REVIEW | RATING
74 32 NY True "Meh." | ✩✩
42 50 WA True "Worked out of the box..." | ✩✩✩✩
57 16 CA NULL "Sick af..." | ✩
... ... ... ... ... | ...
(int) (int) (str) (bool) (str) | (str)

How do we encode the 'RATING' column, an ordinal variable, as a quantitative variable?

  • Transformation: Replace "number of ✩" with "number".
    • This is an ordinal encoding, a transformation that maps ordinal values to the positive integers in a way that preserves order.
    • Example: (freshman, sophomore, junior, senior) -> (0, 1, 2, 3).
    • Important: This transformation preserves "distances" between ratings.
In [22]:
ordinal_enc = {
    '✩': 1,
    '✩✩': 2,
    '✩✩✩': 3,
    '✩✩✩✩': 4,
    '✩✩✩✩✩': 5,
}
ordinal_enc
Out[22]:
{'✩': 1, '✩✩': 2, '✩✩✩': 3, '✩✩✩✩': 4, '✩✩✩✩✩': 5}
In [23]:
ratings = pd.DataFrame().assign(RATING=['✩', '✩✩', '✩✩✩', '✩✩', '✩✩✩', '✩', '✩✩✩', '✩✩✩✩', '✩✩✩✩✩'])
ratings
Out[23]:
RATING
0 ✩
1 ✩✩
2 ✩✩✩
... ...
6 ✩✩✩
7 ✩✩✩✩
8 ✩✩✩✩✩

9 rows × 1 columns

In [24]:
ratings.replace(ordinal_enc)
Out[24]:
RATING
0 1
1 2
2 3
... ...
6 3
7 4
8 5

9 rows × 1 columns

Encoding nominal features¶

UID AGE STATE HAS_BOUGHT REVIEW | RATING
74 32 NY True "Meh." | ✩✩
42 50 WA True "Worked out of the box..." | ✩✩✩✩
57 16 CA NULL "Sick af..." | ✩
... ... ... ... ... | ...
(int) (int) (str) (bool) (str) | (str)

How do we encode the 'STATE' column, a nominal variable, as a quantitative variable? In other words, how do we turn 'STATE's into meaningful numbers?

  • Question: Why can't we use an ordinal encoding, e.g. NY -> 0, WA -> 1?
  • Answer: There is no inherent ordering to states, e.g. WA is not inherently "more" of anything than NY.
  • We've already seen the correct strategy: one hot encoding.

Example: Horsepower 🚗¶

The following dataset, built into the seaborn plotting library, contains various information about (older) cars.

In [25]:
mpg = sns.load_dataset('mpg').dropna()
mpg.head()
Out[25]:
mpg cylinders displacement horsepower ... acceleration model_year origin name
0 18.0 8 307.0 130.0 ... 12.0 70 usa chevrolet chevelle malibu
1 15.0 8 350.0 165.0 ... 11.5 70 usa buick skylark 320
2 18.0 8 318.0 150.0 ... 11.0 70 usa plymouth satellite
3 16.0 8 304.0 150.0 ... 12.0 70 usa amc rebel sst
4 17.0 8 302.0 140.0 ... 10.5 70 usa ford torino

5 rows × 9 columns

We really do mean old:

In [26]:
mpg['model_year'].value_counts()
Out[26]:
73    40
78    36
76    34
      ..
71    27
80    27
74    26
Name: model_year, Length: 13, dtype: int64

Let's investigate the relationship between 'horsepower' and 'mpg'.

The relationship between 'horsepower' and 'mpg'¶

In [27]:
px.scatter(mpg, x='horsepower', y='mpg')
  • It appears that there is a negative association between 'horsepower' and 'mpg', though it's not quite linear.
  • Let's try and fit a simple linear model that uses 'horsepower' to predict 'mpg' and see what happens.

Predicting 'mpg' using 'horsepower'¶

In [28]:
car_model = LinearRegression()
car_model.fit(mpg[['horsepower']], mpg['mpg'])
Out[28]:
LinearRegression()

What do our predictions look like?

In [29]:
hp_points = pd.DataFrame({'horsepower': [25, 225]})
fig = px.scatter(mpg, x='horsepower', y='mpg')
fig.add_trace(go.Scatter(
    x=hp_points['horsepower'],
    y=car_model.predict(hp_points),
    mode='lines',
    name='Predicted MPG using Horsepower'
))

Our regression line doesn't capture the curvature in the relationship between 'horsepower' and 'mpg'.

Let's look at the residuals:

In [30]:
res = mpg.assign(
    Predictions=car_model.predict(mpg[['horsepower']]),
    Residuals=mpg['mpg'] - car_model.predict(mpg[['horsepower']]),
)
fig = px.scatter(res, x='Predictions', y='Residuals')
fig.add_hline(0, line_width=3, opacity=1)
In [34]:
car_model.score(mpg[['horsepower']], mpg['mpg'])
Out[34]:
0.6059482578894348

Linearization¶

The Tukey Mosteller Bulge Diagram helps us pick which transformations to apply to data in order to linearize it.

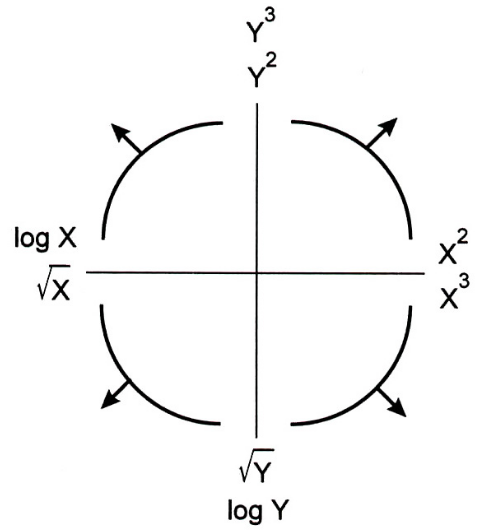
No description has been provided for this image

The bottom-left quadrant appears to match the shape of the scatter plot between 'horsepower' and 'mpg' the best – let's try taking the log of 'horsepower' ($X$).

In [31]:
mpg['log hp'] = np.log(mpg['horsepower'])

What does our data look like now?

In [32]:
px.scatter(mpg, x='log hp', y='mpg')

Predicting 'mpg' using log('horsepower')¶

Let's fit another linear model.

In [33]:
car_model_log = LinearRegression()
car_model_log.fit(mpg[['log hp']], mpg['mpg'])
Out[33]:
LinearRegression()

What do our predictions look like now?

In [34]:
fig = px.scatter(mpg, x='log hp', y='mpg')
log_hp_points = pd.DataFrame({'log hp': [3.7, 5.5]})
fig = px.scatter(mpg, x='log hp', y='mpg')
fig.add_trace(go.Scatter(
    x=log_hp_points['log hp'],
    y=car_model_log.predict(log_hp_points),
    mode='lines',
    name='Predicted MPG using log(Horsepower)'
))

The fit looks a bit better! How about the $R^2$?

In [35]:
car_model_log.score(mpg[['log hp']], mpg['mpg'])
Out[35]:
0.6683347641192137

Also a bit better!

What do our predictions look like on the original, non-transformed scatter plot? Let's see:

In [36]:
fig = px.scatter(mpg, x='horsepower', y='mpg')
fig.add_trace(
    go.Scatter(
        x=mpg['horsepower'], 
        y=car_model_log.intercept_ + car_model_log.coef_[0] * np.log(mpg['horsepower']),  
        mode='markers', name='Predicted MPG using log(Horsepower)'
    )
)
fig

Our predictions that used $\log(\text{Horsepower})$ as an input don't fall on a straight line. We shouldn't expect them to; the red dots come from:

$$\text{Predicted MPG} = 108.698 - 18.582 \cdot \log(\text{Horsepower})$$

In [37]:
car_model_log.intercept_, car_model_log.coef_
Out[37]:
(108.69970699574483, array([-18.58]))

Quantitative scaling¶

Until now, feature transformations we've discussed so far have involved converting categorical variables into quantitative variables. However, our log transformation was an example of transforming a quantitative variable into a new quantitative variable; this practice is called quantitative scaling.

  • Standardization: $x_i \rightarrow \frac{x_i - \bar{x}}{\sigma_x}$.
  • Linearization via a non-linear transformation: e.g. $\text{log}$ and $\text{sqrt}$. See Lab 8 for more.
  • Discretization: Convert data into percentiles (or more generally, quantiles).

Question 🤔 (Answer at q.dsc80.com)

What questions do you have?

The modeling process¶

The modeling process¶

  1. Create, or engineer, features to best reflect the "meaning" behind data.
  1. Choose a model that is appropriate to capture the relationships between features ($X$) and the target/response ($y$).
  1. Choose a loss function, e.g. squared loss.
  1. Fit the model: that is, minimize empirical risk to find optimal model parameters $w^*$.
  1. Evaluate the model, e.g. using RMSE or $R^2$.

We can perform all of the above directly in sklearn!

No description has been provided for this image

preprocessing and linear_models¶

For the feature engineering step of the modeling pipeline, we will use sklearn's preprocessing module.

No description has been provided for this image

For the model creation step of the modeling pipeline, we will use sklearn's linear_model module, as we've already seen. linear_model.LinearRegression is an example of an estimator class.

No description has been provided for this image

Transformers in sklearn¶

Transformer classes¶

  • Transformers take in "raw" data and output "processed" data. They are used for creating features.
  • The input to a transformer should be a multi-dimensional numpy array.
    • Inputs can be DataFrames, but sklearn only looks at the values (i.e. it calls to_numpy() on input DataFrames).
  • The output of a transformer is a numpy array (never a DataFrame or Series).
  • Transformers, like most relevant features of sklearn, are classes, not functions, meaning you need to instantiate them and call their methods.

Example: Predicting tips 🧑‍🍳¶

We'll continue working with our trusty tips dataset.

In [42]:
tips.head()
Out[42]:
total_bill tip sex smoker ... time size smoker == Yes smoker == No
0 3.07 1.00 Female Yes ... Dinner 1 1 0
1 18.78 3.00 Female No ... Dinner 2 0 1
2 26.59 3.41 Male Yes ... Dinner 3 1 0
3 14.26 2.50 Male No ... Lunch 2 0 1
4 21.16 3.00 Male No ... Lunch 2 0 1

5 rows × 9 columns

Example transformer: Binarizer¶

The Binarizer transformer allows us to map a quantitative sequence to a sequence of 1s and 0s, depending on whether values are above or below a threshold.

Property Example Description
Initialize with parameters binar = Binarizer(thresh) set x=1 if x > thresh, else 0
Transform data in a dataset feat = binar.transform(data) Binarize all columns in data

First, we need to import the relevant class from sklearn.preprocessing. (Tip: import just the relevant classes you need from sklearn.)

In [38]:
from sklearn.preprocessing import Binarizer

Let's try binarizing 'total_bill'. We'll say a "large" bill is one that is strictly greater than $20.

In [44]:
tips['total_bill'].head()
Out[44]:
0     3.07
1    18.78
2    26.59
3    14.26
4    21.16
Name: total_bill, dtype: float64

First, we initialize a Binarizer object with the threshold we want.

In [39]:
bi = Binarizer(threshold=20)

Then, we call bi's transform method and pass it the data we'd like to transform. Note that its input and output are both 2D.

In [40]:
transformed_bills = bi.transform(tips[['total_bill']]) # Must give transform a 2D array/DataFrame.
transformed_bills[:5]

/Users/bt/miniforge3/envs/dsc80/lib/python3.8/site-packages/sklearn/base.py:443: UserWarning:

X has feature names, but Binarizer was fitted without feature names
Out[40]:
array([[0.],
       [0.],
       [1.],
       [0.],
       [1.]])

Example transformer: StandardScaler¶

  • StandardScaler standardizes data using the mean and standard deviation of the data.

$$z(x_i) = \frac{x_i - \text{mean of } x}{\text{SD of } x}$$

  • Unlike Binarizer, StandardScaler requires some knowledge (mean and SD) of the dataset before transforming.
  • As such, we need to fit an StandardScaler transformer before we can use the transform method.
  • Typical usage: fit transformer on a sample, use that fit transformer to transform future data.

Example transformer: StandardScaler¶

It only makes sense to standardize the already-quantitative features of tips, so let's select just those.

In [44]:
tips_quant = tips[['total_bill', 'size']]
tips_quant.head()
Out[44]:
total_bill size
0 3.07 1
1 18.78 2
2 26.59 3
3 14.26 2
4 21.16 2

Let's initialize a StandardScaler object.

In [46]:
from sklearn.preprocessing import StandardScaler
In [47]:
stdscaler = StandardScaler()

Note that the following does not work! The error message is very helpful.

In [48]:
stdscaler.transform(tips_quant)

---------------------------------------------------------------------------
NotFittedError                            Traceback (most recent call last)
Cell In[48], line 1
----> 1 stdscaler.transform(tips_quant)

File ~/miniforge3/envs/dsc80/lib/python3.8/site-packages/sklearn/preprocessing/_data.py:970, in StandardScaler.transform(self, X, copy)
    955 def transform(self, X, copy=None):
    956     """Perform standardization by centering and scaling.
    957 
    958     Parameters
   (...)
    968         Transformed array.
    969     """
--> 970     check_is_fitted(self)
    972     copy = copy if copy is not None else self.copy
    973     X = self._validate_data(
    974         X,
    975         reset=False,
   (...)
    980         force_all_finite="allow-nan",
    981     )

File ~/miniforge3/envs/dsc80/lib/python3.8/site-packages/sklearn/utils/validation.py:1222, in check_is_fitted(estimator, attributes, msg, all_or_any)
   1217     fitted = [
   1218         v for v in vars(estimator) if v.endswith("_") and not v.startswith("__")
   1219     ]
   1221 if not fitted:
-> 1222     raise NotFittedError(msg % {"name": type(estimator).__name__})

NotFittedError: This StandardScaler instance is not fitted yet. Call 'fit' with appropriate arguments before using this estimator.

Instead, we need to first call the fit method on stdscaler.

In [49]:
# This is like saying "determine the mean and SD of each column in tips_quant".
stdscaler.fit(tips_quant)
Out[49]:
StandardScaler()

Now, transform will work.

In [50]:
# First column is 'total_bill', second column is 'size'.
tips_quant_z = stdscaler.transform(tips_quant)
tips_quant_z[:5]
Out[50]:
array([[-1.88, -1.65],
       [-0.11, -0.6 ],
       [ 0.77,  0.45],
       [-0.62, -0.6 ],
       [ 0.15, -0.6 ]])

We can also access the mean and variance stdscaler computed for each column:

In [53]:
stdscaler.mean_
Out[53]:
array([19.79,  2.57])
In [54]:
stdscaler.var_
Out[54]:
array([78.93,  0.9 ])

Note that we can call transform on DataFrames other than tips_quant. We will do this often – fit a transformer on one dataset (training data) and use it to transform other datasets (test data).

In [55]:
stdscaler.transform(tips_quant.sample(5))
Out[55]:
array([[ 0.97, -0.6 ],
       [-0.28, -0.6 ],
       [ 1.19,  1.51],
       [-0.49, -0.6 ],
       [ 0.65,  1.51]])

💡 Pro-Tip: Using .fit_transform¶

The .fit_transform method will fit the transformer and then transform the data in one go.

In [51]:
stdscaler.fit_transform(tips_quant)
Out[51]:
array([[-1.88, -1.65],
       [-0.11, -0.6 ],
       [ 0.77,  0.45],
       ...,
       [-0.26, -0.6 ],
       [-1.09, -0.6 ],
       [-0.32,  0.45]])

StandardScaler summary¶

Property Example Description
Initialize with parameters stdscaler = StandardScaler() z-score the data (no parameters)
Fit the transformer stdscaler.fit(X) Compute the mean and SD of X
Transform data in a dataset feat = stdscaler.transform(X_new) z-score X_new with mean and SD of X
Fit and transform stdscaler.fit_transform(X) Compute the mean and SD of X, then z-score X

Example transformer: OneHotEncoder¶

Let's keep just the categorical columns in tips.

In [52]:
tips_cat = tips[['sex', 'smoker', 'day', 'time']]
tips_cat.head()
Out[52]:
sex smoker day time
0 Female Yes Sat Dinner
1 Female No Thur Dinner
2 Male Yes Sat Dinner
3 Male No Thur Lunch
4 Male No Thur Lunch

Like StdScaler, we will need to fit our OneHotEncoder transformer before it can transform anything.

In [53]:
from sklearn.preprocessing import OneHotEncoder
In [54]:
ohe = OneHotEncoder()
ohe.fit(tips_cat)
Out[54]:
OneHotEncoder()

When we try and transform, we get a result we might not expect.

In [55]:
ohe.transform(tips_cat)
Out[55]:
<244x10 sparse matrix of type '<class 'numpy.float64'>'
	with 976 stored elements in Compressed Sparse Row format>

Since the resulting matrix is sparse – most of its elements are 0 – sklearn uses a more efficient representation than a regular numpy array. We can convert to a regular (dense) array:

In [56]:
ohe.transform(tips_cat).toarray()
Out[56]:
array([[1., 0., 0., ..., 0., 1., 0.],
       [1., 0., 1., ..., 1., 1., 0.],
       [0., 1., 0., ..., 0., 1., 0.],
       ...,
       [1., 0., 1., ..., 1., 0., 1.],
       [0., 1., 1., ..., 0., 1., 0.],
       [1., 0., 1., ..., 0., 1., 0.]])

Notice that the column names from tips_cat are no longer stored anywhere (remember, fit converts the input to a numpy array before proceeding).

We can use the get_feature_names_out method on ohe to access the names of the one-hot-encoded columns, though:

In [57]:
ohe.get_feature_names_out() # x0, x1, x2, and x3 correspond to column names in tips_cat.
Out[57]:
array(['sex_Female', 'sex_Male', 'smoker_No', 'smoker_Yes', 'day_Fri',
       'day_Sat', 'day_Sun', 'day_Thur', 'time_Dinner', 'time_Lunch'],
      dtype=object)
In [58]:
pd.DataFrame(ohe.transform(tips_cat).toarray(), 
             columns=ohe.get_feature_names_out()) # If we need a DataFrame back, for some reason.
Out[58]:
sex_Female sex_Male smoker_No smoker_Yes ... day_Sun day_Thur time_Dinner time_Lunch
0 1.0 0.0 0.0 1.0 ... 0.0 0.0 1.0 0.0
1 1.0 0.0 1.0 0.0 ... 0.0 1.0 1.0 0.0
2 0.0 1.0 0.0 1.0 ... 0.0 0.0 1.0 0.0
... ... ... ... ... ... ... ... ... ...
241 1.0 0.0 1.0 0.0 ... 0.0 1.0 0.0 1.0
242 0.0 1.0 1.0 0.0 ... 0.0 0.0 1.0 0.0
243 1.0 0.0 1.0 0.0 ... 0.0 0.0 1.0 0.0

244 rows × 10 columns

Question 🤔 (Answer at q.dsc80.com)

Suppose we have a training set X_train with labels y_train, and we have a test set X_test with labels y_test. If we want to use OHE on the day column, we will use ohe.fit_transform(X_train), but we will NOT do ohe.fit_transform(X_test). Instead, we will ONLY do ohe.transform(X_test). Why?

Pipelines¶

No description has been provided for this image

So far, we've used transformers for feature engineering and models for prediction. We can combine these steps into a single Pipeline.

Pipelines in sklearn¶

From sklearn's documentation:

Pipeline allows you to sequentially apply a list of transformers to preprocess the data and, if desired, conclude the sequence with a final predictor for predictive modeling.

Intermediate steps of the pipeline must be "transforms", that is, they must implement fit and transform methods. The final estimator only needs to implement fit.

  • General template: pl = Pipeline([trans_1, trans_2, ..., model])
    • Note that the model is optional.
  • Once a Pipeline is instantiated, you can fit all steps (transformers and model) using pl.fit(X, y).
  • To make predictions using raw, untransformed data, use pl.predict(X).
  • The actual list we provide Pipeline with must be a list of tuples, where
    • The first element is a "name" (that we choose) for the step.
    • The second element is a transformer or estimator instance.

Our first Pipeline¶

Let's build a Pipeline that:

  • One hot encodes the categorical features in tips.
  • Fits a regression model on the one hot encoded data.
In [59]:
tips_cat = tips[['sex', 'smoker', 'day', 'time']]
tips_cat.head()
Out[59]:
sex smoker day time
0 Female Yes Sat Dinner
1 Female No Thur Dinner
2 Male Yes Sat Dinner
3 Male No Thur Lunch
4 Male No Thur Lunch
In [60]:
from sklearn.pipeline import Pipeline
In [61]:
pl = Pipeline([
    ('one-hot', OneHotEncoder()),
    ('lin-reg', LinearRegression())
])

Now that pl is instantiated, we fit it the same way we would fit the individual steps.

In [62]:
pl.fit(tips_cat, tips['tip'])
Out[62]:
Pipeline(steps=[('one-hot', OneHotEncoder()), ('lin-reg', LinearRegression())])

Now, to make predictions using raw data, all we need to do is use pl.predict:

In [63]:
pl.predict(tips_cat.iloc[:5])
Out[63]:
array([2.92, 3.16, 3.09, 2.83, 2.83])

pl performs both feature transformation and prediction with just a single call to predict!

We can access individual "steps" of a Pipeline through the named_steps attribute:

In [64]:
pl.named_steps
Out[64]:
{'one-hot': OneHotEncoder(), 'lin-reg': LinearRegression()}
In [65]:
pl.named_steps['one-hot'].transform(tips_cat).toarray()
Out[65]:
array([[1., 0., 0., ..., 0., 1., 0.],
       [1., 0., 1., ..., 1., 1., 0.],
       [0., 1., 0., ..., 0., 1., 0.],
       ...,
       [1., 0., 1., ..., 1., 0., 1.],
       [0., 1., 1., ..., 0., 1., 0.],
       [1., 0., 1., ..., 0., 1., 0.]])
In [66]:
pl.named_steps['one-hot'].get_feature_names_out()
Out[66]:
array(['sex_Female', 'sex_Male', 'smoker_No', 'smoker_Yes', 'day_Fri',
       'day_Sat', 'day_Sun', 'day_Thur', 'time_Dinner', 'time_Lunch'],
      dtype=object)
In [67]:
pl.named_steps['lin-reg'].coef_
Out[67]:
array([-0.09,  0.09, -0.04,  0.04, -0.2 , -0.13,  0.14,  0.19,  0.25,
       -0.25])

pl also has a score method, the same way a fit LinearRegression instance does:

In [68]:
# Why is this so low?
pl.score(tips_cat, tips['tip'])
Out[68]:
0.02749679020147533

More sophisticated Pipelines¶

  • In the previous example, we one hot encoded every input column. What if we want to perform different transformations on different columns?
  • Solution: Use a ColumnTransformer.
    • Instantiate a ColumnTransformer using a list of tuples, where:
      • The first element is a "name" we choose for the transformer.
      • The second element is a transformer instance (e.g. OneHotEncoder()).
      • The third element is a list of relevant column names.

Planning our first ColumnTransformer¶

In [70]:
from sklearn.compose import ColumnTransformer

Let's perform different transformations on the quantitative and categorical features of tips (note that we are not transforming 'tip').

In [69]:
tips_features = tips.drop('tip', axis=1)
tips_features.head()
Out[69]:
total_bill sex smoker day time size smoker == Yes smoker == No
0 3.07 Female Yes Sat Dinner 1 1 0
1 18.78 Female No Thur Dinner 2 0 1
2 26.59 Male Yes Sat Dinner 3 1 0
3 14.26 Male No Thur Lunch 2 0 1
4 21.16 Male No Thur Lunch 2 0 1
  • We will leave the 'total_bill' column untouched.
  • To the 'size' column, we will apply the Binarizer transformer with a threshold of 2 (big tables vs. small tables).
  • To the categorical columns, we will apply the OneHotEncoder transformer.
  • In essence, we will create a transformer that reproduces the following DataFrame:
size x0_Female x0_Male x1_No x1_Yes x2_Fri x2_Sat x2_Sun x2_Thur x3_Dinner x3_Lunch total_bill
0 0 1.0 0.0 1.0 0.0 0.0 0.0 1.0 0.0 1.0 0.0 16.99
1 1 0.0 1.0 1.0 0.0 0.0 0.0 1.0 0.0 1.0 0.0 10.34
2 1 0.0 1.0 1.0 0.0 0.0 0.0 1.0 0.0 1.0 0.0 21.01
3 0 0.0 1.0 1.0 0.0 0.0 0.0 1.0 0.0 1.0 0.0 23.68
4 1 1.0 0.0 1.0 0.0 0.0 0.0 1.0 0.0 1.0 0.0 24.59

Building a Pipeline using a ColumnTransformer¶

Let's start by creating our ColumnTransformer.

In [71]:
preproc = ColumnTransformer(
    transformers=[
        ('size', Binarizer(threshold=2), ['size']),
        ('categorical_cols', OneHotEncoder(), ['sex', 'smoker', 'day', 'time'])
    ],
    remainder='passthrough' # Specify what to do with all other columns ('total_bill' here) – drop or passthrough.
)

Now, let's create a Pipeline using preproc as a transformer, and fit it:

In [74]:
pl = Pipeline([
    ('preprocessor', preproc), 
    ('lin-reg', LinearRegression())
])
In [75]:
pl.fit(tips_features, tips['tip'])
Out[75]:
Pipeline(steps=[('preprocessor',
                 ColumnTransformer(remainder='passthrough',
                                   transformers=[('size',
                                                  Binarizer(threshold=2),
                                                  ['size']),
                                                 ('categorical_cols',
                                                  OneHotEncoder(),
                                                  ['sex', 'smoker', 'day',
                                                   'time'])])),
                ('lin-reg', LinearRegression())])

Prediction is as easy as calling predict:

In [76]:
tips_features.head()
Out[76]:
total_bill sex smoker day time size smoker == Yes smoker == No
0 3.07 Female Yes Sat Dinner 1 1 0
1 18.78 Female No Thur Dinner 2 0 1
2 26.59 Male Yes Sat Dinner 3 1 0
3 14.26 Male No Thur Lunch 2 0 1
4 21.16 Male No Thur Lunch 2 0 1
In [80]:
# Note that we fit the Pipeline using tips_features, not tips_features.head()!
pl.predict(tips_features.head())
Out[80]:
array([1.16, 2.81, 3.7 , 2.4 , 3.07])

Aside: FunctionTransformer¶

A transformer you'll often use as part of a ColumnTransformer is the FunctionTransformer, which enables you to use your own functions on entire columns. Think of it as the sklearn equivalent of apply.

In [77]:
from sklearn.preprocessing import FunctionTransformer
In [78]:
f = FunctionTransformer(np.sqrt)
f.transform([1, 2, 3])
Out[78]:
array([1.  , 1.41, 1.73])

Summary, next time¶

Summary¶

  • To transform a categorical nominal variable into a quantitative variable, use one hot encoding.
  • To transform a categorical ordinal variable into a quantitative variable, use an ordinal encoding.
  • Quantitative feature transformations allow us to use linear models to model non-linear data.
  • Pipelines are powerful because they allow you to perform feature engineering and training/prediction all through a single object.
  • As we'll see next time, they also allow us to easily compare models against each other.

Next time¶

  • More examples of, and ways to create, Pipelines.
  • Multicollinearity.
  • Generalization.