from dsc80_utils import *

This notebook contains code (e.g. the answers to exercises) that was written live during Lecture 13. If you haven't already watched and work through this lecture, you might find it more beneficial to look at the "blank" version of this lecture and answer the exercises yourself.

Lecture 13 – Linear Regression

DSC 80, Winter 2024

Announcements 📣

• The Project 3 Checkpoint is due today.
  • The full project is due on Thursday, February 29th.
• Lab 7 is due on Monday, February 26th.
• Project 4 will likely be released over the weekend.

Come to the HDSI undergraduate social tomorrow!

Diversity in Data Science (DDS) and the faculty DEI committee are jointly hosting an undergraduate social tomorrow (Friday 2/23) from 3-5PM on the HDSI patio.

Come to socialize with your fellow classmates and faculty – I'll be there the whole time, and so will free food!

Agenda 📆

• Modeling.
• Case study: Restaurant tips 🧑‍🍳.
• Regression in sklearn.

Conceptually, today will mostly be review from DSC 40A, but we'll introduce a few new practical tools that we'll build upon next week.

Question 🤔 (Answer at q.dsc80.com)

Remember, you can always ask questions at q.dsc80.com!

Exercise

Taken from the Spring 2022 Final Exam.

The DataFrame below contains a corpus of four song titles, labeled from 0 to 3.

	track_name
0	i hate you i love you i hate that i love you
1	love me like a love song
2	love you better
3	hate sosa

Part 1: What is the TF-IDF of the word "hate" in Song 0's title? Use base 2 in your logarithm, and give your answer as a simplified fraction.

tf-idf("hate", Song 0) = tf("hate", Song 0) x idf("hate")

tf("hate", Song 0) = $\frac{2}{12} = \frac{1}{6}$

idf("hate") = $\log_2 (\frac{4}{2}) = \log_2 2 = 1$

tf-idf("hate", Song 0) = tf("hate", Song 0) x idf("hate") = $\frac{1}{6} \cdot 1 = \boxed{\frac{1}{6}}$

Exercise

Part 2: Which word in Song 0's title has the highest TF-IDF?

The word 'i' – it is the most common word in Song 0's title, and doesn't appear in any other document's title.

Exercise

Part 3: Let $\text{tfidf}(t, d)$ be the TF-IDF of term $t$ in document $d$, and let $\text{bow}(t, d)$ be the number of occurrences of term $t$ in document $d$.

Select all correct answers below.

• If $\text{tfidf}(t, d) = 0$, then $\text{bow}(t, d) = 0$.
• If $\text{bow}(t, d) = 0$, then $\text{tfidf}(t, d) = 0$.
• Neither of the above statements are necessarily true.

The first statement is wrong! If $t$ is in every document, then $\text{idf}(t) = \log(\frac{n}{n}) = \log(1) = 0$.

The second statement is true!

Exercise

Part 4: Below, we've encoded the corpus from the previous page using the bag-of-words model.

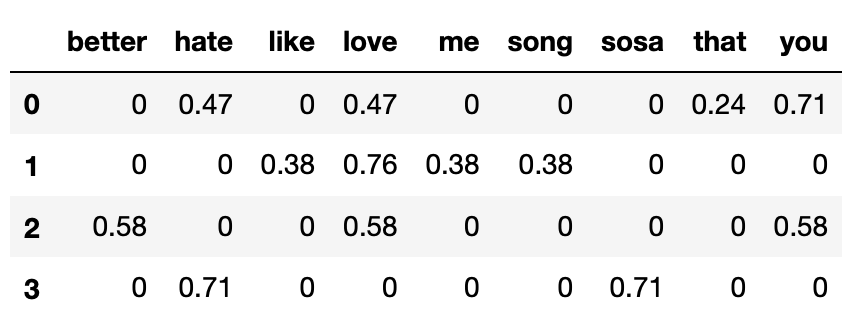
Note that in the above DataFrame, each row has been normalized to have a length of 1 (i.e. $|\vec{v}| = 1$ for all four row vectors).

Which song's title has the highest cosine similarity with Song 0's title?

$$\cos \theta = \frac{\vec{a} \cdot \vec{b}}{| \vec{a} | | \vec{b} |}$$

• Row 0 and 1: $0.47 \cdot 0.76$
• Row 0 and 2: $0.47 \cdot 0.58 + 0.71 \cdot 0.58$
• Row 0 and 3: $0.47 \cdot 0.71$

Answer: Song 2.

Modeling

Reflection

So far this quarter, we've learned how to:

• Extract information from tabular data using pandas and regular expressions.

• Clean data so that it best represents an underlying data generating process.
  • Missingness analyses and imputation.

• Collect data from the internet through scraping and APIs, and parse it using BeautifulSoup.

• Perform exploratory data analysis through aggregation, visualization, and the computation of summary statistics like TF-IDF.

• Infer about the relationships between samples and populations through hypothesis and permutation testing.

• Now, let's make predictions.

Modeling

• A model is a set of assumptions about how data were generated.

• George Box, a famous statistician, once said "All models are wrong, but some are useful." What did he mean?

Philosophy

"It has been said that "all models are wrong but some models are useful." In other words, any model is at best a useful fiction—there never was, or ever will be, an exactly normal distribution or an exact linear relationship. Nevertheless, enormous progress has been made by entertaining such fictions and using them as approximations."

"Since all models are wrong the scientist cannot obtain a "correct" one by excessive elaboration. On the contrary following William of Occam he should seek an economical description of natural phenomena. Just as the ability to devise simple but evocative models is the signature of the great scientist so overelaboration and overparameterization is often the mark of mediocrity."

Goals of modeling

1. To make accurate predictions regarding unseen data.

   • Given this dataset of past UCSD data science students' salaries, can we predict your future salary? (regression)
   • Given this dataset of images, can we predict if this new image is of a dog, cat, or zebra? (classification)

2. To make inferences about complex phenomena in nature.

   • Is there a linear relationship between the heights of children and the heights of their biological mothers?
   • The weights of smoking and non-smoking mothers' babies babies in my sample are different – how confident am I that this difference exists in the population?

• Of the two focuses of models, we will focus on prediction.

• In the above taxonomy, we will focus on supervised learning.

• We'll start with regression before moving to classification.

Features

• A feature is a measurable property of a phenomenon being observed.
  • Other terms for "feature" include "(explanatory) variable" and "attribute".
  • Typically, features are the inputs to models.

• In DataFrames, features typically correspond to columns, while rows typically correspond to different individuals.

• Some features come as part of a dataset, e.g. weight and height, but others we need to create given existing features, for example:

$$\text{BMI} = \frac{\text{weight (kg)}}{\text{[height (m)]}^2}$$

• Example: TF-IDF creates features that summarize documents!

Example: Restaurant tips 🧑‍🍳

About the data

What features does the dataset contain? Is this likely a recent dataset, or an older one?

# The dataset is built into plotly!
tips = px.data.tips()
tips

	total_bill	tip	sex	smoker	day	time	size
0	16.99	1.01	Female	No	Sun	Dinner	2
1	10.34	1.66	Male	No	Sun	Dinner	3
2	21.01	3.50	Male	No	Sun	Dinner	3
...	...	...	...	...	...	...	...
241	22.67	2.00	Male	Yes	Sat	Dinner	2
242	17.82	1.75	Male	No	Sat	Dinner	2
243	18.78	3.00	Female	No	Thur	Dinner	2

244 rows × 7 columns

Predicting tips

• Goal: Given various information about a table at a restaurant, we want to predict the tip that a server will earn.

• Why might a server be interested in doing this?
  • To determine which tables are likely to tip the most (inference).
  • To predict earnings over the next month (prediction).

Exploratory data analysis

• The most natural feature to look at first is total bills.

• As such, we should explore the relationship between total bills and tips. Moving forward:
  • $x$: Total bills.
  • $y$: Tips.

fig = tips.plot(kind='scatter', x='total_bill', y='tip', title='Tip vs. Total Bill')
fig.update_layout(xaxis_title='Total Bill', yaxis_title='Tip')

Model #1: Constant

• Let's start simple, by ignoring all features. Suppose our model assumes every tip is given by a constant dollar amount:

$$\text{tip} = h^{\text{true}}$$

• Model: There is a single tip amount $h^{\text{true}}$ that all customers pay.
  • Correct? No!
  • Useful? Perhaps. An estimate of $h^{\text{true}}$, denoted by $h^*$, can allow us to predict future tips.

Estimating $h^{\text{true}}$

• The true parameter $h^{\text{true}}$ is determined by the universe. We'll never get to see it, so we need to estimate it.

• There are several ways we could estimate $h^{\text{true}}$. For instance, we could use domain knowledge: for instance, assume that everyone clicks the $1 tip option when buying coffee.

• But, perhaps, we should look at the tips that we've already seen in our dataset to estimate $h^{\text{true}}$.

Looking at the data

Our estimate for $h^{\text{true}}$ should be a good summary statistic of the distribution of tips.

fig = tips.plot(kind='hist', x='tip', title='Distribution of Tip', nbins=20)
fig.update_layout(xaxis_title='Tip', yaxis_title='Frequency')

Empirical risk minimization

• In DSC 40A, we established a framework for estimating model parameters:
  • Choose a loss function, which measures how "good" a single prediction is.
  • Minimize empirical risk, to find the best estimate for the dataset that we have.

• Depending on which loss function we choose, we will end up with different $h^*$ (which are estimates of $h^{\text{true}})$.

• If we choose squared loss, then our empirical risk is mean squared error:

$$\text{MSE} = \frac{1}{n} \sum_{i = 1}^n ( y_i - h )^2 \overset{\text{calculus}}\implies h^* = \text{mean}(y)$$ Remember, tips are our $y$ variable.

• If we choose absolute loss, then our empirical risk is mean absolute error:

$$\text{MAE} = \frac{1}{n} \sum_{i = 1}^n | y_i - h | \overset{\text{algebra}}\implies h^* = \text{median}(y)$$

The mean tip

Let's suppose we choose squared loss, meaning that $h^* = \text{mean}(y)$.

mean_tip = tips['tip'].mean()
mean_tip

2.99827868852459

$h^* = 2.998$ is our fit model – it was fit to our training data (the data we have available to learn from).

Let's visualize this prediction.

fig = px.scatter(tips, x='total_bill', y='tip')
fig.add_hline(mean_tip, line_width=3, line_color='orange', opacity=1)
fig.update_layout(title='Tip vs. Total Bill',
                  xaxis_title='Total Bill', yaxis_title='Tip')

Note that to make predictions, this model ignores total bill (and all other features), and predicts the same tip for all tables.

The quality of predictions

• Question: How can we quantify how good this constant prediction is at predicting tips in our training data – that is, the data we used to fit the model?

• One answer: use the mean squared error. If $y_i$ represents the $i$th actual value and $H(x_i)$ represents the $i$th predicted value, then:

$$\text{MSE} = \frac{1}{n} \sum_{i = 1}^n \big( y_i - H(x_i) \big)^2$$

np.mean((tips['tip'] - mean_tip) ** 2)

1.9066085124966412

# The same! A fact from 40A.
np.var(tips['tip'])

1.9066085124966412

• Issue: The units of MSE are "dollars squared", which are a little hard to interpret.

Root mean squared error

• Often, to measure the quality of a regression model's predictions, we will use the root mean squared error (RMSE):

$$\text{RMSE} = \sqrt{\frac{1}{n} \sum_{i = 1}^n \big( y_i - H(x_i) \big)^2}$$

• The units of the RMSE are the same as the units of the original $y$ values – dollars, in this case.

• Important: Minimizing MSE is the same as minimizing RMSE; the constant tip $h^*$ that minimizes MSE is the same $h^*$ that minimizes RMSE. (Why?)

Computing and storing the RMSE

Since we'll compute the RMSE for our future models too, we'll define a function that can compute it for us.

def rmse(actual, pred):
    return np.sqrt(np.mean((actual - pred) ** 2))

Let's compute the RMSE of our constant tip's predictions, and store it in a dictionary that we can refer to later on.

rmse(tips['tip'], mean_tip)

1.3807999538298954

mean_tip # A single number!

2.99827868852459

rmse_dict = {}
rmse_dict['constant tip amount'] = rmse(tips['tip'], mean_tip)
rmse_dict

{'constant tip amount': 1.3807999538298954}

Key idea: Since the mean minimizes RMSE for the constant model, it is impossible to change the mean_tip argument above to another number and yield a lower RMSE.

Question 🤔 (Answer at q.dsc80.com)

Remember, you can always ask questions at q.dsc80.com!

Model #2: Simple linear regression using total bill

• We haven't yet used any of the features in the dataset. The first natural feature to look at is 'total_bill'.

tips.head()

	total_bill	tip	sex	smoker	day	time	size
0	16.99	1.01	Female	No	Sun	Dinner	2
1	10.34	1.66	Male	No	Sun	Dinner	3
2	21.01	3.50	Male	No	Sun	Dinner	3
3	23.68	3.31	Male	No	Sun	Dinner	2
4	24.59	3.61	Female	No	Sun	Dinner	4

• We can fit a simple linear model to predict tips as a function of total bills:

$$\text{predicted tip} = w_0 + w_1 \cdot \text{total bill}$$

• This is a reasonable thing to do, because total bills and tips appeared to be linearly associated when we visualized them on a scatter plot a few slides ago.

Recap: Simple linear regression

A simple linear regression model is a linear model with a single feature, as we have here. For any total bill $x_i$, the predicted tip $H(x_i)$ is given by

$$H(x_i) = w_0 + w_1x_i$$

• Question: How do we determine which intercept, $w_0$, and slope, $w_1$, to use?

• One answer: Pick the $w_0$ and $w_1$ that minimize mean squared error. If $x_i$ and $y_i$ correspond to the $i$th total bill and tip, respectively, then:

$$\begin{align*}\text{MSE} &= \frac{1}{n} \sum_{i = 1}^n \big( y_i - H(x_i) \big)^2 \\ &= \frac{1}{n} \sum_{i = 1}^n \big( y_i - w_0 - w_1x_i \big)^2\end{align*}$$

• Key idea: The lower the MSE on our training data is, the "better" the model fits the training data.
  • Lower MSE = better predictions.
  • But lower MSE ≠ more reflective of reality!

Empirical risk minimization, by hand

$$\begin{align*}\text{MSE} &= \frac{1}{n} \sum_{i = 1}^n \big( y_i - w_0 - w_1x_i \big)^2\end{align*}$$

• In DSC 40A, you found the formulas for the best intercept, $w_0^*$, and the best slope, $w_1^*$, through calculus.
  • The resulting line, $H(x_i) = w_0^* + w_1^* x_i$, is called the line of best fit, or the regression line.

• Specifically, if $r$ is the correlation coefficient, $\sigma_x$ and $\sigma_y$ are the standard deviations of $x$ and $y$, and $\bar{x}$ and $\bar{y}$ are the means of $x$ and $y$, then:

$$w_1^* = r \cdot \frac{\sigma_y}{\sigma_x}$$$$w_0^* = \bar{y} - w_1^* \bar{x}$$

Regression in sklearn

sklearn

• sklearn (scikit-learn) implements many common steps in the feature and model creation pipeline.
  • It is widely used throughout industry and academia.

• It interfaces with numpy arrays, and to an extent, pandas DataFrames.

• Huge benefit: the documentation online is excellent.

The LinearRegression class

• sklearn comes with several subpackages, including linear_model and tree, each of which contains several classes of models.

• We'll start with the LinearRegression class from linear_model.

from sklearn.linear_model import LinearRegression

• Important: From the documentation, we have:

LinearRegression fits a linear model with coefficients w = (w1, …, wp) to minimize the residual sum of squares between the observed targets in the dataset, and the targets predicted by the linear approximation.

In other words, **`LinearRegression` minimizes mean squared error by default**! (Per the documentation, it also includes an intercept term by default.)

LinearRegression?

Fitting a simple linear model

First, we must instantiate a LinearRegression object and fit it. By calling fit, we are saying "minimize mean squared error on this dataset and find $w^*$."

model = LinearRegression()

# Note that there are two arguments to fit – X and y!
# (It is not necessary to write X= and y=)
model.fit(X=tips[['total_bill']], y=tips['tip']);

After fitting, we can access $w^*$ – that is, the best slope and intercept.

# w_1*
model.coef_[0]

0.10502451738435332

# w_0*
model.intercept_

0.920269613554674

These coefficients tell us that the "best way" (according to squared loss) to make tip predictions using a linear model is using:

$$\text{predicted tip} = 0.92 + 0.105 \cdot \text{total bill}$$

This model predicts that people tip by:

• Tipping a constant 92 cents.
• Tipping 10.5% for every dollar spent.

This is the best "linear" pattern in the dataset – it doesn't mean this is actually how people tip!

Let's visualize this model, along with our previous model.

line_pts = pd.DataFrame({'total_bill': [0, 60]})

fig = px.scatter(tips, x='total_bill', y='tip')
fig.add_trace(go.Scatter(
    x=line_pts['total_bill'],
    y=[mean_tip, mean_tip],
    mode='lines',
    name='Constant Model (Mean Tip)'
))
fig.add_trace(go.Scatter(
    x=line_pts['total_bill'],
    y=model.predict(line_pts),
    mode='lines',
    name='Linear Model: Total Bill Only'
))
fig.update_layout(title='Tip vs. Total Bill',
                  xaxis_title='Total Bill', 
                  yaxis_title='Tip')

Visually, our linear model seems to be a better fit for our dataset than our constant model.

Can we quantify whether or not it is better? Does it better reflect reality?

Making predictions

Fit LinearRegression objects also have a predict method, which can be used to predict tips for any total bill, new or old.

model.predict([[15]])

/Users/surajrampure/miniforge3/envs/dsc80/lib/python3.8/site-packages/sklearn/base.py:450: UserWarning:

X does not have valid feature names, but LinearRegression was fitted with feature names

array([2.5])

# Since we trained on a DataFrame, the input to model.predict should also
# be a DataFrame. To avoid having to do this, we can use .to_numpy()
# when specifying X= and y=.
test_points = pd.DataFrame({'total_bill': [15, 4, 100]})
model.predict(test_points)

array([ 2.5 ,  1.34, 11.42])

Comparing models

If we want to compute the RMSE of our model on the training data, we need to find its predictions on every row in the training data, tips.

all_preds = model.predict(tips[['total_bill']])
all_preds

array([2.7 , 2.01, 3.13, ..., 3.3 , 2.79, 2.89])

rmse_dict['one feature: total bill'] = rmse(tips['tip'], all_preds)
rmse_dict

{'constant tip amount': 1.3807999538298954,
 'one feature: total bill': 1.0178504025697377}

• The RMSE of our simple linear model is lower than that of our constant model, which means it does a better job at predicting tips in our training data than our constant model.

• Theory tells us it's impossible for the RMSE on the training data to increase as we add more features to the same model. However, the RMSE may increase on unseen data by adding more features; we'll discuss this idea more soon.

Question 🤔 (Answer at q.dsc80.com)

Remember, you can always ask questions at q.dsc80.com!

Model #3: Multiple linear regression using total bill and table size

• There are still many features in tips we haven't touched:

tips.head()

	total_bill	tip	sex	smoker	day	time	size
0	16.99	1.01	Female	No	Sun	Dinner	2
1	10.34	1.66	Male	No	Sun	Dinner	3
2	21.01	3.50	Male	No	Sun	Dinner	3
3	23.68	3.31	Male	No	Sun	Dinner	2
4	24.59	3.61	Female	No	Sun	Dinner	4

• Let's try using another feature – table size. Such a model would predict tips using:

$$\text{predicted tip} = w_0 + w_1 \cdot \text{total bill} + w_2 \cdot \text{table size}$$

Multiple linear regression

To find the optimal parameters $w^*$, we will again use sklearn's LinearRegression class. The code is not all that different!

model_two = LinearRegression()
model_two.fit(X=tips[['total_bill', 'size']], y=tips['tip'])

LinearRegression()

# w_0*
model_two.intercept_

0.6689447408125035

# w_1*
model_two.coef_[0]

0.09271333683226951

# w_2*
model_two.coef_[1]

0.19259779439078667

test_pts = pd.DataFrame({'total_bill': [25], 'size': [4]})
model_two.predict(test_pts)

array([3.76])

What does this model look like?

Plane of best fit ✈️

Here, we must draw a 3D scatter plot and plane, with one axis for total bill, one axis for table size, and one axis for tip. The code below does this.

XX, YY = np.mgrid[0:50:2, 0:8:1]
Z = model_two.intercept_ + model_two.coef_[0] * XX + model_two.coef_[1] * YY
plane = go.Surface(x=XX, y=YY, z=Z, colorscale='Oranges')

fig = go.Figure(data=[plane])
fig.add_trace(go.Scatter3d(x=tips['total_bill'], 
                           y=tips['size'], 
                           z=tips['tip'], mode='markers', marker = {'color': '#656DF1'}))

fig.update_layout(scene=dict(xaxis_title='Total Bill',
                             yaxis_title='Table Size',
                             zaxis_title='Tip'),
                  title='Tip vs. Total Bill and Table Size',
                  width=1000, height=500)

Comparing models, again

How does our two-feature linear model stack up to our single feature linear model and our constant model?

rmse_dict['two features'] = rmse(
    tips['tip'], model_two.predict(tips[['total_bill', 'size']])
)

rmse_dict

{'constant tip amount': 1.3807999538298954,
 'one feature: total bill': 1.0178504025697377,
 'two features': 1.007256127114662}

• The RMSE of our two-feature model is the lowest of the three models we've looked at so far, but not by much. We didn't gain much by adding table size to our linear model.

• It's also not clear whether table sizes are practically useful in predicting tips.
  • We already have the total amount the table spent; why do we need to know how many people were there?

Residual plots

• From DSC 10: one important technique for diagnosing model fit is the residual plot.

• The $i$th residual is $ y_i - H(x_i) $.

• A residual plot has
  • predicted values $H(x)$ on the $x$-axis, and
  • residuals $ y - H(x) $ on the $y$-axis.

# Let's start with the single-variable model:
with_resid = tips.assign(**{
    'Predicted Tip': model.predict(tips[['total_bill']]),
    'Residual': tips['tip'] - model.predict(tips[['total_bill']]),
})
fig = px.scatter(with_resid, x='Predicted Tip', y='Residual')
fig.add_hline(0, line_width=2, opacity=1).update_layout(title='Residual Plot (Simple Linear Model)')

• If all assumptions about linear regression hold, then residual plot should look randomly scattered around the horizontal line $y = 0$.

• Here, we see that the model makes bigger mistakes for larger predicted values. But overall, there's no apparent trend, so a linear model seems appropriate.

# What about the two-variable model?
with_resid = tips.assign(**{
    'Predicted Tip': model_two.predict(tips[['total_bill', 'size']]),
    'Residual': tips['tip'] - model_two.predict(tips[['total_bill', 'size']]),
})
fig = px.scatter(with_resid, x='Predicted Tip', y='Residual')
fig.add_hline(0, line_width=2, opacity=1).update_layout(title='Residual Plot (Multiple Regression)')

Looks about the same as the previous plot!

Question 🤔 (Answer at q.dsc80.com)

Remember, you can always ask questions at q.dsc80.com!

The .score method of a LinearRegression object

Model objects in sklearn that have already been fit have a score method.

model_two.score(tips[['total_bill', 'size']], tips['tip'])

0.46786930879612587

That doesn't look like the RMSE... what is it? 🤔

We'll find out next time!

Summary, next time

Summary

• We built three models:
  • A constant model: $\text{predicted tip} = h^*$.
  • A simple linear regression model: $\text{predicted tip} = w_0^* + w_1^* \cdot \text{total bill}$.
  • A multiple linear regression model: $\text{predicted tip} = w_0^* + w_1^* \cdot \text{total bill} + w_2^* \cdot \text{table size}$.
• As we added more features, our RMSEs decreased.
  • This was guaranteed to happen, since we were only looking at our training data.
• It is not clear that the final linear model is actually "better"; it doesn't seem to reflect reality better than the previous models.

LinearRegression summary

Property	Example	Description
Initialize model parameters	lr = LinearRegression()	Create (empty) linear regression model
Fit the model to the data	lr.fit(X, y)	Determines regression coefficients
Use model for prediction	lr.predict(X_new)	Uses regression line to make predictions
Evaluate the model	lr.score(X, y)	Calculates the $R^2$ of the LR model
Access model attributes	lr.coef_, lr.intercept_	Accesses the regression coefficients and intercept

Next time

tips.head()

	total_bill	tip	sex	smoker	day	time	size
0	16.99	1.01	Female	No	Sun	Dinner	2
1	10.34	1.66	Male	No	Sun	Dinner	3
2	21.01	3.50	Male	No	Sun	Dinner	3
3	23.68	3.31	Male	No	Sun	Dinner	2
4	24.59	3.61	Female	No	Sun	Dinner	4

• So far, in our journey to predict 'tip', we've only used the existing numerical features in our dataset, 'total_bill' and 'size'.

• There's a lot of information in tips that we didn't use – 'sex', 'smoker', 'day', and 'time', for example. We can't use these features in their current form, because they're non-numeric.

• How do we use categorical features in a regression model?