from dsc80_utils import *
import lec15_util as util

Lecture 15 – Standardization, Multicollinearity, and Generalization

DSC 80, Winter 2024

Earlier today.

Announcements 📣

• Project 3 is due tonight.
• Lab 8 is due on Monday, March 4th.
• Project 4 is released! Read all about it at dsc80.com/proj04.
  • The checkpoint is due on Thursday, March 7th.
  • The full project is due on Thursday, March 21st. You cannot use slip days on the final deadline.
• The Final Exam is on Tuesday, March 19th from 3-6PM.
  • Practice by working through old exams at practice.dsc80.com.

RSVP to the senior capstone showcase on March 15th!

The senior capstone showcase is on Friday, March 15th in the Price Center East Ballroom. The DSC seniors will be presenting posters on their capstone projects. Come and ask them questions; if you're a DSC major, this will be you one day!

Last year's showcase.

The session is broken into two blocks:

• Block 1: 11AM-12:30PM.
• Block 2: 1-2:30PM.

Look at the list of topics and RSVP at hdsishowcase.com!

Agenda 📆

• Standardization.
• Multicollinearity.
• Generalization.
  • Bias and variance.
  • Train-test splits.

Today's lecture will be mostly theoretical!

Question 🤔 (Answer at q.dsc80.com)

Remember, you can always ask questions at q.dsc80.com!

Standardization

Review: Transformers, models, and Pipelines

Last class, we learned how to build a Pipeline in sklearn. A Pipeline consists of:

• transformers (from sklearn.preprocessing), which engineer features, and

• a model (from sklearn.linear_model), which is trained to make predictions.

Let's import the necessary classes and functions from sklearn.

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.metrics import mean_squared_error # New!

Let's also re-import our trusty tips DataFrame.

import seaborn as sns
tips = sns.load_dataset('tips')
tips.head()

	total_bill	tip	sex	smoker	day	time	size
0	16.99	1.01	Female	No	Sun	Dinner	2
1	10.34	1.66	Male	No	Sun	Dinner	3
2	21.01	3.50	Male	No	Sun	Dinner	3
3	23.68	3.31	Male	No	Sun	Dinner	2
4	24.59	3.61	Female	No	Sun	Dinner	4

An example Pipeline

One of the transformers we used was the StandardScaler transformer, which standardizes columns.

$$z(x_i) = \frac{x_i - \text{mean of } x}{\text{SD of } x}$$

Let's build a Pipeline that:

• Takes in the 'total_bill' and 'size' features of tips.
• Standardizes those features.
• Uses the resulting standardized features to fit a linear model that predicts 'tip'.

# Let's define these once, since we'll use them repeatedly.
X = tips[['total_bill', 'size']]
y = tips['tip']

model_with_std = Pipeline([
    ('standardize', StandardScaler()),
    ('lin-reg', LinearRegression())
])


model_with_std.fit(X, y)

Pipeline(steps=[('standardize', StandardScaler()),
                ('lin-reg', LinearRegression())])

How well does our model do? We can compute its $R^2$ and RMSE.

model_with_std.score(X, y)

0.46786930879612587

mean_squared_error(y, model_with_std.predict(X), squared=False)

1.007256127114662

Does this model perform any better than one that doesn't standardize its features? Let's find out.

model_without_std = LinearRegression()
model_without_std.fit(X, y)

LinearRegression()

model_without_std.score(X, y)

0.46786930879612587

mean_squared_error(y, model_without_std.predict(X), squared=False)

1.007256127114662

No!

The purpose of standardizing features

If you're performing "vanilla" linear regression – that is, using the LinearRegression object – then standardizing your features will not change your model's performance.

• There are other models where standardizing your features will improve performance, because the methods assume features are standardized.
  • Regularized linear regression (see DSC 140A).
  • PCA (assumes centered data, not necessarily standardized: see DSC 140B).
  • Clustering algorithms, e.g. $k$-means clustering (saw in DSC 40A!).

• There is a benefit to standardizing features when performing vanilla linear regression, as we saw in DSC 40A: the features are brought to the same scale, so the coefficients can be compared directly.

# Total bill, table size.
model_without_std.coef_

array([0.09, 0.19])

# Total bill, table size.
model_with_std.named_steps['lin-reg'].coef_

array([0.82, 0.18])

Multicollinearity

Heights and weights

We have a dataset containing the weights and heights of 25,000 18 year olds, taken from here.

people_path = Path('data') / 'SOCR-HeightWeight.csv'
people = pd.read_csv(people_path).drop(columns=['Index'])
people.head()

	Height (Inches)	Weight (Pounds)
0	65.78	112.99
1	71.52	136.49
2	69.40	153.03
3	68.22	142.34
4	67.79	144.30

people.plot(kind='scatter', x='Height (Inches)', y='Weight (Pounds)', 
            title='Weight vs. Height for 25,000 18 Year Olds')

Motivating example

Suppose we fit a simple linear regression model that uses height in inches to predict weight in pounds.

$$\text{predicted weight (pounds)} = w_0 + w_1 \cdot \text{height (inches)}$$

X = people[['Height (Inches)']]
y = people['Weight (Pounds)']

lr_one_feat = LinearRegression()
lr_one_feat.fit(X, y)

LinearRegression()

$w_0^*$ and $w_1^*$ are shown below, along with the model's training set RMSE.

lr_one_feat.intercept_, lr_one_feat.coef_

(-82.57574306454093, array([3.08]))

mean_squared_error(y, lr_one_feat.predict(X), squared=False)

10.079113675632819

Now, suppose we fit another regression model, that uses height in inches AND height in centimeters to predict weight.

$$\text{predicted weight (pounds)} = w_0 + w_1 \cdot \text{height (inches)} + w_2 \cdot \text{height (cm)}$$

people['Height (cm)'] = people['Height (Inches)'] * 2.54 # 1 inch = 2.54 cm

X2 = people[['Height (Inches)', 'Height (cm)']]

lr_two_feat = LinearRegression()
lr_two_feat.fit(X2, y)

LinearRegression()

What are $w_0^*$, $w_1^*$, $w_2^*$, and the model's test RMSE?

lr_two_feat.intercept_, lr_two_feat.coef_

(-82.57525639659859, array([ 3.38e+10, -1.33e+10]))

mean_squared_error(y, lr_two_feat.predict(X2), squared=False)

10.079113677131511

Observation: The intercept is the same as before (roughly -82.57), as is the RMSE. However, the coefficients on 'Height (Inches)' and 'Height (cm)' are massive in size!

What's going on?

Redundant features

Let's use simpler numbers for illustration. Suppose in the first model, $w_0^* = -80$ and $w_1^* = 3$.

$$\text{predicted weight (pounds)} = -80 + 3 \cdot \text{height (inches)}$$

In the second model, we have:

$$\begin{align*}\text{predicted weight (pounds)} &= w_0^* + w_1^* \cdot \text{height (inches)} + w_2^* \cdot \text{height (cm)} \\ &= w_0^* + w_1^* \cdot \text{height (inches)} + w_2^* \cdot \big( 2.54^* \cdot \text{height (inches)} \big) \\ &= w_0^* + \left(w_1^* + 2.54 \cdot w_2^* \right) \cdot \text{height (inches)} \end{align*}$$

In the first model, we already found the "best" intercept ($-80$) and slope ($3$) in a linear model that uses height in inches to predict weight.

So, as long as $w_1^* + 2.54 \cdot w_2^* = 3$ in the second model, the second model's training predictions will be the same as the first, and hence they will also minimize RMSE.

Infinitely many parameter choices

Issue: There are an infinite number of $w_1^*$ and $w_2^*$ that satisfy $w_1^* + 2.54 \cdot w_2^* = 3$!

$$\text{predicted weight} = -80 - 10 \cdot \text{height (inches)} + \frac{13}{2.54} \cdot \text{height (cm)}$$

$$\text{predicted weight} = -80 + 10 \cdot \text{height (inches)} - \frac{7}{2.54} \cdot \text{height (cm)}$$

• Both prediction rules look very different, but actually make the same predictions.

• lr.coef_ could return either set of coefficients, or any other of the infinitely many options.

• But neither set of coefficients is has any meaning!

(-80 - 10 * people.iloc[:, 0] + (13 / 2.54) * people.iloc[:, 2]).head()

0    117.35
1    134.55
2    128.20
3    124.65
4    123.36
dtype: float64

(-80 + 10 * people.iloc[:, 0] - (7 / 2.54) * people.iloc[:, 2]).head()

0    117.35
1    134.55
2    128.20
3    124.65
4    123.36
dtype: float64

Multicollinearity

• Multicollinearity occurs when features in a regression model are highly correlated with one another.
  • In other words, multicollinearity occurs when a feature can be predicted using a linear combination of other features, fairly accurately.

• When multicollinearity is present in the features, the coefficients in the model are uninterpretable – they have no meaning.
  • A "slope" represents "the rate of change of $y$ with respect to a feature", when all other features are held constant – but if there's multicollinearity, you can't hold other features constant.

• Note: Multicollinearity doesn't impact a model's predictions!
  • It doesn't impact a model's ability to generalize to unseen data.
  • If features are multicollinear in the training data, they will probably be multicollinear in the test data too.

• Solutions:
  • Manually remove highly correlated features.
  • Use a dimensionality reduction technique (such as PCA) to automatically reduce dimensions.

Example: One hot encoding

A one hot encoding will result in multicollinearity unless you drop one of the one hot encoded features.

Suppose we have the following fitted model:

$$ \begin{aligned} H(x) = 1 + 2 \cdot (\text{smoker==Yes}) - 2 \cdot (\text{smoker==No}) \end{aligned} $$

This is equivalent to:

$$ \begin{aligned} H(x) = 10 - 7 \cdot (\text{smoker==Yes}) - 11 \cdot (\text{smoker==No}) \end{aligned} $$

Solution: Drop one of the one hot encoded columns. sklearn.preprocessing.OneHotEncoder has an option to do this.

Aside: Pipelines of just transformers

If you want to apply multiple transformations to the same column in a dataset, you can create a Pipeline just for that column.

For example, suppose we want to:

• One hot encode the 'sex', 'smoker', and 'time' columns, dropping one column per feature.
• One hot encode the 'day' column, but as either 'Weekday', 'Sat', or 'Sun', again, dropping one column per feature.
• Binarize the 'size' column.

Here's how we might do that:

def is_weekend(s):
    # The input to is_weekend is a Series!
    return s.replace({'Thur': 'Weekday', 'Fri': 'Weekday'})

from sklearn.preprocessing import Binarizer, FunctionTransformer, OneHotEncoder
from sklearn.compose import ColumnTransformer

pl_day = Pipeline([
    ('is-weekend', FunctionTransformer(is_weekend)),
    ('ohe', OneHotEncoder(drop='first'))
])

col_trans = ColumnTransformer([
    ('transform-day', pl_day, ['day']),
    ('ohe-others', OneHotEncoder(drop='first'), ['sex', 'smoker', 'time']),
    ('binarize-size', Binarizer(threshold=2), ['size'])
], remainder='passthrough')

pl = Pipeline([
    ('transf', col_trans),
    ('lin-reg', LinearRegression())
])

pl.fit(tips.drop('tip', axis=1), tips['tip'])

Pipeline(steps=[('transf',
                 ColumnTransformer(remainder='passthrough',
                                   transformers=[('transform-day',
                                                  Pipeline(steps=[('is-weekend',
                                                                   FunctionTransformer(func=<function is_weekend at 0x164182af0>)),
                                                                  ('ohe',
                                                                   OneHotEncoder(drop='first'))]),
                                                  ['day']),
                                                 ('ohe-others',
                                                  OneHotEncoder(drop='first'),
                                                  ['sex', 'smoker', 'time']),
                                                 ('binarize-size',
                                                  Binarizer(threshold=2),
                                                  ['size'])])),
                ('lin-reg', LinearRegression())])

How many coefficients does the resulting linear model have?

pl.named_steps['lin-reg'].coef_

array([ 0.12,  0.13, -0.03, -0.09, -0.05,  0.27,  0.1 ])

Key takeaways

• Multicollinearity is present in a linear model when one feature can be accurately predicted using one or more other features.
  • In other words, it is present when a feature is redundant.

• Multicollinearity doesn't pose an issue for prediction; it doesn't hinder a model's ability to generalize. Instead, it renders the coefficients of a linear model meaningless.

Question 🤔 (Answer at q.dsc80.com)

Remember, you can always ask questions at q.dsc80.com!

Exercise

Taken from Problem 9 on the Fall 2023 Final Exam.

Generalization

Motivation

• You and Billy are studying for an upcoming exam. You both decide to test your understanding by taking a practice exam.
  • Your logic: If you do well on the practice exam, you should do well on the real exam.

• You each take the practice exam once and look at the solutions afterwards.

• Your strategy: Memorize the answers to all practice exam questions, e.g. "Question 1: A; Question 2: C; Question 3: A."

• Billy's strategy: Learn high-level concepts from the solutions, e.g. "data are NMAR if the likelihood of missingness depends on the missing values themselves."

• Who will do better on the practice exam? Who will probably do better on the real exam? 🧐

Evaluating the quality of a model

• So far, we've computed the RMSE (and $R^2$) of our fit regression models on the data that we used to fit them, i.e. the training data.

• We've said that Model A is better than Model B if Model A's RMSE is lower than Model B's RMSE.
  • Remember, our training data is a sample from some population.
  • Just because a model fits the training data well doesn't mean it will generalize and work well on similar, unseen samples from the same population!

Example: Overfitting and underfitting

Let's collect two samples $\{(x_i, y_i)\}$ from the same population.

np.random.seed(23) # For reproducibility.

def sample_from_pop(n=100):
    x = np.linspace(-2, 3, n)
    y = x ** 3 + (np.random.normal(0, 3, size=n))
    return pd.DataFrame({'x': x, 'y': y})

sample_1 = sample_from_pop()
sample_2 = sample_from_pop()

For now, let's just look at Sample 1. The relationship between $x$ and $y$ is roughly cubic; that is, $y \approx x^3$ (remember, in reality, you won't get to see the population).

px.scatter(sample_1, x='x', y='y', title='Sample 1')

Polynomial regression

Let's fit three polynomial models on Sample 1:

• Degree 1.
• Degree 3.
• Degree 25.

The PolynomialFeatures transformer will be helpful here.

from sklearn.preprocessing import PolynomialFeatures

# fit_transform fits and transforms the same input.
d2 = PolynomialFeatures(3)
d2.fit_transform(np.array([1, 2, 3, 4, -2]).reshape(-1, 1))

array([[ 1.,  1.,  1.,  1.],
       [ 1.,  2.,  4.,  8.],
       [ 1.,  3.,  9., 27.],
       [ 1.,  4., 16., 64.],
       [ 1., -2.,  4., -8.]])

Below, we look at our three models' predictions on Sample 1 (which they were trained on).

# Look at the definition of train_and_plot in lec15_util.py if you're curious as to how the plotting works.
fig = util.train_and_plot(train_sample=sample_1, test_sample=sample_1, degs=[1, 3, 25], data_name='Sample 1')
fig.update_layout(title='Trained on Sample 1, Performance on Sample 1')

The degree 25 polynomial has the lowest RMSE on Sample 1.

How do the same fit polynomials look on Sample 2?

fig = util.train_and_plot(train_sample=sample_1, test_sample=sample_2, degs=[1, 3, 25], data_name='Sample 2')
fig.update_layout(title='Trained on Sample 1, Performance on Sample 2')

• The degree 3 polynomial has the lowest RMSE on Sample 2.

• Note that we didn't get to see Sample 2 when fitting our models!

• As such, it seems that the degree 3 polynomial generalizes better to unseen data than the degree 25 polynomial does.

What if we fit a degree 1, degree 3, and degree 25 polynomial on Sample 2 as well?

util.plot_multiple_models(sample_1, sample_2, degs=[1, 3, 25])

Key idea: Degree 25 polynomials seem to vary more when trained on different samples than degree 3 and 1 polynomials do.

Bias and variance

The training data we have access to is a sample from the population. We are concerned with our model's ability to generalize and work well on different datasets drawn from the same population.

Suppose we fit a model $H$ (e.g. a degree 3 polynomial) on several different datasets from a population. There are three sources of error that arise:

• ⭐️ Bias: The expected deviation between a predicted value and an actual value.
  • In other words, for a given $x_i$, how far is $H(x_i)$ from the true $y_i$, on average?
  • Low bias is good! ✅
  • High bias is a sign of underfitting, i.e. that our model is too basic to capture the relationship between our features and response.

• ⭐️ Model variance ("variance"): The variance of a model's predictions.
  • In other words, for a given $x_i$, how much does $H(x_i)$ vary across all datasets?
  • Low model variance is good! ✅
  • High model variance is a sign of overfitting, i.e. that our model is too complicated and is prone to fitting to the noise in our training data.

• Observation error: The error due to the random noise in the process we are trying to model (e.g. measurement error). We can't control this, without collecting more data!

Here, suppose:

• The red bulls-eye represents your true weight and height 🧍.
• The dark blue darts represent predictions of your weight and height using different models that were fit on the same DGP.

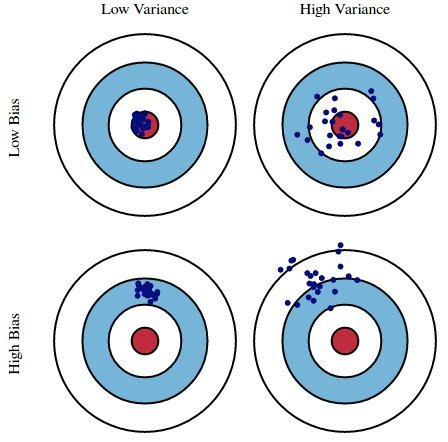
We'd like our models to be in the top left, but in practice that's hard to achieve!

Risk vs. empirical risk

• In DSC 40A, we started using empirical risk minimization to find optimal model parameters $w^*$:

$$ \text{choose the $w$ such that } \frac{1}{n} \sum_{i = 1}^n \left( y_i - H(x_i) \right)^2 \text{ is minimized}$$or, equivalently: $$w^* = \underset{w}{\text{argmin}} \frac{1}{n} \sum_{i = 1}^n \left( y_i - H(x_i) \right)^2$$

• Key idea: A model that works well on past data should work well on future data, if future data looks like past data.

• What we really want is for the expected loss for a new data point $(x_{\text{new}}, y_{\text{new}})$, drawn from the same population as the training set, to be small. That is, we want $$\mathbb{E}[y_{\text{new}} - H(x_{\text{new}})]^2$$ to be minimized. The quantity above is called risk.

• What's that fancy $\mathbb{E}$? It is the expectation operator of a random variable: it computes the average value of the random variable across its entire distribution.
  • (From Math 183/180A) If $X \sim \text{Binomial}(n, p)$, then $\mathbb{E}[X] = np$.

• In general, we don't know the entire population distribution of $x$s and $y$s, so we can't compute risk exactly. That's why we compute empirical risk!

$$\mathbb{E}[y_{\text{new}} - H(x_{\text{new}})]^2 \approx \frac{1}{n} \sum_{i = 1}^n \left( y_i - H(x_i) \right)^2$$

The bias-variance decomposition

Risk can be decomposed as follows:

$$\mathbb{E}[y_{\text{new}} - H(x_{\text{new}})]^2 = \text{model bias}^2 + \text{model variance} + \text{observation error}$$

• Remember, this expectation $\mathbb{E}$ is over the entire population of $x$s and $y$s: in real life, we don't know what this population distribution is, so we can't put actual numbers to this.

• If $H$ is too simple to capture the relationship between $x$s and $y$s in the population, $H$ will underfit to training sets and have high bias.

• If $H$ is overly complex, $H$ will overfit to training sets and have high variance, meaning it will change significantly from one training set to the next.

• Generally:
  • Training error reflects bias, not variance.
  • Test error reflects both bias and variance.

Navigating the bias-variance tradeoff

$$\mathbb{E}[y_{\text{new}} - H(x_{\text{new}})]^2 = \text{model bias}^2 + \text{model variance} + \text{observation error}$$

• As we collect more data points (i.e. as $n \uparrow$):
  • Model variance decreases.
  • If $H$ can exactly model the true population relationship between $x$ and $y$ (e.g. cubic), then model bias also decreases.
  • If $H$ can't exactly model the true population relationship between $x$ and $y$, then model bias will remain large.

• As we add more features (i.e. as $d \uparrow$):
  • Model variance increases, whether or not the feature was useful.
  • Adding a useful feature decreases model bias.
  • Adding a useless feature doesn't change model bias.

• Example: suppose the actual relationship between $x$ and $y$ in the population is linear, and we fit $H$ using simple linear regression.
  • Model bias = 0.
  • Model variance $\propto \frac{d}{n}$.
    • As $d \uparrow$, model variance $\uparrow$.
    • As $n \uparrow$, model variance $\downarrow$.

Read more here.

Question 🤔 (Answer at q.dsc80.com)

Remember, you can always ask questions at q.dsc80.com!

Train-test splits

Avoiding overfitting

• We won't know whether our model has overfit to our sample (training data) unless we get to see how well it performs on a new sample from the same population.

• 💡Idea: Split our sample into a training set and test set.

• Use only the training set to fit the model (i.e. find $w^*$).

• Use the test set to evaluate the model's error (RMSE, $R^2$).

• The test set is like a new sample of data from the same population as the training data!

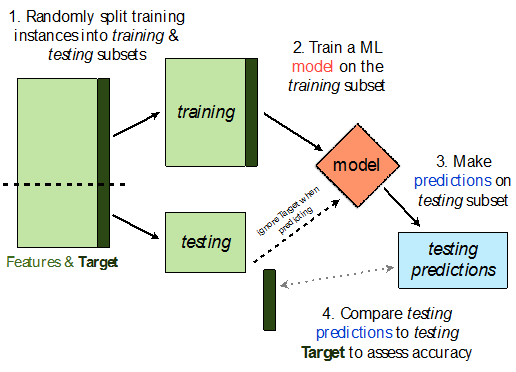
Train-test split 🚆

sklearn.model_selection.train_test_split implements a train-test split for us! 🙏🏼

If X is an array/DataFrame of features and y is an array/Series of responses,

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)

randomly splits the features and responses into training and test sets, such that the test set contains 0.25 of the full dataset.

from sklearn.model_selection import train_test_split

# Read the documentation!
train_test_split?

Let's perform a train/test split on our tips dataset.

X = tips.drop('tip', axis=1)
y = tips['tip']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) # We don't have to choose 0.25.

Before proceeding, let's check the sizes of X_train and X_test.

print('Rows in X_train:', X_train.shape[0])
display(X_train.head())
print('Rows in X_test:', X_test.shape[0])
display(X_test.head())

Rows in X_train: 195

	total_bill	sex	smoker	day	time	size
4	24.59	Female	No	Sun	Dinner	4
209	12.76	Female	Yes	Sat	Dinner	2
178	9.60	Female	Yes	Sun	Dinner	2
230	24.01	Male	Yes	Sat	Dinner	4
5	25.29	Male	No	Sun	Dinner	4

Rows in X_test: 49

	total_bill	sex	smoker	day	time	size
146	18.64	Female	No	Thur	Lunch	3
224	13.42	Male	Yes	Fri	Lunch	2
134	18.26	Female	No	Thur	Lunch	2
131	20.27	Female	No	Thur	Lunch	2
147	11.87	Female	No	Thur	Lunch	2

X_train.shape[0] / tips.shape[0]

0.7991803278688525

Example train-test split

Steps:

1. Fit a model on the training set.
2. Evaluate the model on the test set.

tips.head()

	total_bill	tip	sex	smoker	day	time	size
0	16.99	1.01	Female	No	Sun	Dinner	2
1	10.34	1.66	Male	No	Sun	Dinner	3
2	21.01	3.50	Male	No	Sun	Dinner	3
3	23.68	3.31	Male	No	Sun	Dinner	2
4	24.59	3.61	Female	No	Sun	Dinner	4

X = tips[['total_bill', 'size']] # For this example, we'll use just the already-quantitative columns in tips.
y = tips['tip']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1) # random_state is like np.random.seed.

Here, we'll use a stand-alone LinearRegression model without a Pipeline, but this process would work the same if we were using a Pipeline.

lr = LinearRegression()
lr.fit(X_train, y_train)

LinearRegression()

Let's check our model's performance on the training set first.

pred_train = lr.predict(X_train)
rmse_train = mean_squared_error(y_train, pred_train, squared=False)
rmse_train

0.9803205287924736

And the test set:

pred_test = lr.predict(X_test)
rmse_test = mean_squared_error(y_test, pred_test, squared=False)
rmse_test

1.1381771291131253

Since rmse_train and rmse_test are similar, it doesn't seem like our model is overfitting to the training data. If rmse_test was much larger than rmse_train, it would be evidence that our model is unable to generalize well.

Hyperparameters

Example: Polynomial regression

We recently looked at an example of polynomial regression.

fig = util.train_and_plot(train_sample=sample_1, test_sample=sample_2, degs=[1, 3, 25], data_name='Sample 2')
fig.update_layout(title='Trained on Sample 1, Performance on Sample 2')

When building these models:

• We got to choose the degree of the polynomials (i.e. we chose 1, 3, and 25).
• We didn't get to choose the exact formulas for the three polynomials – their formulas were learned from data.

Parameters vs. hyperparameters

• A parameter defines the relationship between variables in a model.

  • We learn parameters from data.
  • For instance, suppose we fit a degree 3 polynomial to data, and end up with

  $$H(x) = 1 - 2x + 13x^2 - 4x^3$$

  • 1, -2, 13, and -4 are parameters.

• A hyperparameter is a parameter that we get to choose before our model is fit to the data.
  • Think of hyperparameters as knobs 🎛 – we get to pick and tune them!
  • Polynomial degree was a hyperparameter in the previous example, and we tried three different values: 1, 3, and 25.

• Question: How do we choose the "right" hyperparameter(s)?

Training error vs. test error

• We know that a model's performance on a test set is a good estimate of its ability to generalize to unseen data.

• We want to find the hyperparameter that leads to the best test set performance.

• Idea:
  1. Come up with a list of hyperparameters to try.
  2. For each hyperparameter, train the model on the training set and compute its performance on the test set.
  3. Pick the hyperparameter with the best performance on the test set.

Training error vs. test error

• Let's try this strategy on Sample 1 from our earlier example.

• We'll try to fit a polynomial model on the dataset; we'll choose the polynomial's degree from the list [1, 2, ..., 25].

px.scatter(sample_1, x='x', y='y', title='Sample 1')

First, we perform a train-test split.

X = sample_1[['x']]
y = sample_1['y']

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=100)

💡 Pro-Tip: Using make_pipeline

Instead of using the Pipeline class directly, you can use make_pipeline for a more compact syntax:

(Also, there's an analogous sklearn.compose.make_column_transformer for the ColumnTransformer class.)

from sklearn.pipeline import Pipeline, make_pipeline
from sklearn.preprocessing import PolynomialFeatures

# Pipeline with degree-2 polynomial features
pl = Pipeline([('poly', PolynomialFeatures(2)), ('lin-reg', LinearRegression())])

# Same pipeline, notice that make_pipeline generates names for pipeline steps
pl = make_pipeline(PolynomialFeatures(2), LinearRegression())
pl

Pipeline(steps=[('polynomialfeatures', PolynomialFeatures()),
                ('linearregression', LinearRegression())])

Polynomial degree vs. train/test error

Now, we'll create models with degree-1 through degree-25 polynomial features and compute their train and test errors.

train_errs = []
test_errs = []

for d in range(1, 26):
    pl = make_pipeline(PolynomialFeatures(d), LinearRegression())
    pl.fit(X_train, y_train)
    train_errs.append(mean_squared_error(y_train, pl.predict(X_train), squared=False))
    test_errs.append(mean_squared_error(y_test, pl.predict(X_test), squared=False))

errs = pd.DataFrame({'Train Error': train_errs, 'Test Error': test_errs})

Let's look at the plots of training error vs. degree and test error vs. degree.

fig = px.line(errs)
fig.update_layout(showlegend=True, xaxis_title='Polynomial Degree', yaxis_title='RMSE')

• Training error appears to decrease as polynomial degree increases.

• Test error appears to decrease until a "valley", and then increases again.

• Here, we'd choose a degree of 3, since that degree has the lowest test error.

Training error vs. test error

The pattern we saw in the previous example is true more generally.

We pick the hyperparameter(s) at the "valley" of test error.

Note that training error tends to underestimate test error, but it doesn't have to – i.e., it is possible for test error to be lower than training error (say, if the test set is "easier" to predict than the training set).

Conducting train-test splits

• Recall, training data is used to fit our model, and test data is used to evaluate our model.

• Question: How should we split?
  • sklearn's train_test_split splits randomly, which usually works well.
  • However, if there is some element of time in the training data (say, when predicting the future price of a stock), a better split is "past" and "future".

• Question: How large should the split be, e.g. 90%-10% vs. 75%-25%?
  • There's a tradeoff – a larger training set should lead to a "better" model, while a larger test set should lead to a better estimate of our model's ability to generalize.
  • There's no "right" choice, but we usually choose between 10% to 25% for the test set.

But wait...

• With our current strategy, we are choosing the hyperparameter that creates the model that performs best on the test set.

• As such, we are overfitting to the test set – the best hyperparameter for the test set might not be the best hyperparameter for a totally unseen dataset!

• It seems like we need another split.

Summary, next time

Summary

• We want to build models that generalize well to unseen data.
  • Models that have high bias are too simple to represent complex relationships in data, and underfit.
  • Models that have high variance are overly complex for the relationships in the data, and vary a lot when fit on different datasets. Such models overfit to the training data.
• A model's training error tends to decrease as model complexity increases, while its test error tends to decrease, before reaching a "sweet spot" and increasing again.
• A hyperparameter is a configuration that we choose before training a model; an important task in machine learning is selecting "good" hyperparameters.

Next time

We can't choose model hyperparameters just by using a train-test split, because this strategy overfits to the test data.

Is there a better way to choose model hyperparameters? Yes: cross-validation.