Midterm 02

Suppose a hash table is constructed so that collisions are resolved through chaining. The hash table has \(10\) bins, and 100 items are inserted into the hash table.

True or False: it is possible for one of the bins to contain all 100 items.

Suppose a hash table in constructed so that collisions are resolved through chaining. The hash table has a number of bins \(k\) that is \(\Theta(n)\), where \(n\) is the number of elements being stored in the hash table; that is, the hash table grows as more elements are inserted.

Suppose the hash function uses only the first \(k / 2\) bins of the hash table, but appears to hash items into these bins evenly.

What is the expected time complexity of a membership query on this hash table? State your answer in asymptotic notation in terms of the number of elements in the hash table, \(n\).

Consider the code below:

def intersection(A, B):
    common = set()
    for x in A:
        if x in B:
            common.add(x)
    return common

What is the expected time complexity of this code if A and B are Python sets (hash tables) with \(n\) elements each? State your answer as a function of \(n\) using asymptotic notation. You may assume that the hash function used is ``good'' in that it hashes evenly (that is, it satisfies the simple universal hashing assumption).

An undirected graph has 5 nodes. What is the greatest number of edges it can have?

A directed graph has 10 edges. What is the smallest number of nodes it can have?

An undirected graph with 20 nodes and 30 edges has three connected components: \(A\), \(B\), and \(C\). Connected component \(A\) has 7 nodes. What is the smallest number of edges it can have?

Let \(v = \{a, b, c, d, e, f, g\}\) and \(E = \{(a,g), (b,d), (d, e), (f, d)\}\). How many connected components does the undirected graph \(G =(V, E)\) have?

Let \(G = (V, E)\) be a directed graph with \(|V| > 1\). Suppose that every node in \(G\) is reachable from every other node. True or False: each node in the graph must have an out-degree of at least one and an in-degree of at least one.

Let \(G\) be an undirected graph, and let \(u, v,\) and \(z\) be three nodes in the graph. Consider the problem of finding a shortest path from \(u\) to \(v\) which passes through node \(z\).

True or False: a shortest path from \(u\) to \(v\) passing through \(z\) may include node \(u\) twice.

An isolated node in an undirected graph is a node that has no neighbors.

Suppose a graph \(G = (V, E)\) is represented using an adjacency matrix. What is the best possible worst-case time complexity of an efficient algorithm for computing the number of isolated nodes in the graph? State your answer as a function of \(|V|\) and \(|E|\) using asymptotic notation.

Consider running a breadth-first search (BFS) on the graph shown below, using node \(s\) as the source and adopting the convention that neighbors are produced in ascending order by label.

How many nodes will be popped from the queue before node \(u_8\) is popped?

Suppose that a breadth-first search on an undirected graph \(G\) is paused and the queue is printed. Suppose that every node in the queue is either distance 5 from the source, or distance 6. At this moment, node \(u\) is undiscovered.

True or False: it is possible that node \(u\) is distance 4 from the source.

Suppose a breadth-first search (BFS) is performed in order to calculate a dictionary of shortest path distances, dist, from a source node \(s\) to all nodes reachable from \(s\) in an undirected graph \(G = (V, E)\).

Suppose node \(u\) is a node in \(G\), and \(v_1\) and \(v_2\) are two neighbors of node \(u\). Assume that \(u\) is reachable from \(s\).

Define a circle graph with \(n\) nodes to be an undirected graph \(G = (V, E)\) with nodes \(u_1, u_2, \ldots, u_n\) and edges \((u_1, u_2), (u_2, u_3), \ldots, (u_{n-1}, u_n)\), along with one additional edge \((u_n, u_1)\) completing the cycle. An example of a circle graph with 6 nodes is shown below:

What is the time complexity of breath-first search when run on a circle graph with \(n\) nodes? State your answer as a function of \(n\) using asymptotic notation.

Consider the code below, which is a modification of the code for bfs given in lecture:

from collections import deque

def modified_full_bfs(graph):
    status = {node: 'undiscovered' for node in graph.nodes}
    for node in graph.nodes:
        if status[node] == 'undiscovered':
            modified_bfs(graph, node, status)

def modified_bfs(graph, source, status=None):
    """Start a BFS at `source`."""
    if status is None:
        status = {node: 'undiscovered' for node in graph.nodes}

    status[source] = 'pending'
    pending = deque([source])

    # while there are still pending nodes
    while pending: 
        u = pending.popleft()
        for v in graph.neighbors(u):
            # explore edge (u,v)
            if status[v] == 'undiscovered':
                status[v] = 'pending'
                # append to right
                pending.append(v)
                for z in graph.nodes:   # <----- new line!
                    print(z, status[z]) # <----- new line!

        status[u] = 'visited'

Notice the two new lines; these lines print all node statuses any time that an undiscovered node has been found.

What is the time complexity of this modified modified_full_bfs? State your answer in asymptotic notation in terms of the number of nodes, \(|V|\), and the number of edges, \(|E|\). You may assume that the graph is represented using an adjacency list.

Consider calling full_bfs on a directed graph, and recall that full_bfs will make calls to bfs until all nodes have been marked as visited.

True or False: the number of calls made to bfs depends on the order in which graph.nodes produces the graph's nodes. That is, if nodes are produced in a different order, the number of calls to bfs may be different.

Suppose a depth-first search (DFS) is run on the graph shown below using node \(s\) as the source and adopting the convention that a node's neighbors are produced in ascending order of their label.

Let \(G\) be a graph, and suppose \(s\), \(u\), and \(v\) are three nodes in the graph.

Suppose a depth-first search (DFS) is run on \(G\) using node \(s\) as the source and adopting the convention that a node's neighbors are produced in ascending order by label. During this DFS, start and finish times are computed. Suppose it is found that:

Now suppose another DFS is run using node \(s\) as the source, but adopting a different convention about the order in which neighbors are produced. Suppose new_start and new_finish are the start and finish times found by this second DFS. True or False: it must be that

Consider the graph \(G = (V, E)\) with \(V = \{a, b, c\}\) and \(E = \{(a, b)\}\).

How many valid topological sorts of this graph are there?

Suppose we define a forward-looking graph with \(n\) nodes to be the directed graph \(G = (V, E)\) with nodes \(u_1, \ldots, u_n\) and the edge \((u_i, u_j)\) if and only if \(i < j\). An example of such a graph with 4 nodes is shown below.

What is the time complexity of depth-first search when run on a forward-looking graph with \(n\) nodes, using node \(u_1\) as the source? State your answer as a function of \(n\) using asymptotic notation.

Suppose an undirected graph \(G = (V, E)\) is a tree with 33 edges. Suppose a node \(s\) is used as the source of a depth-first search.

Including the root call of dfs on node \(s\), how many calls to dfs will be made?

Let \(G = (V, E)\) be an undirected tree.

Suppose breadth-first search (BFS) and depth-first search (DFS) are each run on the graph using the same source node. True or False: for any node \(u\) in the graph, the BFS predecessor of \(u\) and the DFS predecessor of \(u\) must be the same.

Recall that the outer loop of the Bellman-Ford algorithm without early stopping loops for a fixed number of iterations, while the inner loop iterates over each edge of the graph.

Suppose Bellman-Ford with early stopping is run on the graph below using node \(s\) as the source:

What is the fewest number of iterations of the outer loop that can possibly be performed?

Recall that the Bellman-Ford algorithm keeps track of the estimated shortest path distance from the source to each node in the graph. These estimates are updated, and eventually become correct, provided that the graph has no negative cycles.

Suppose the Bellman-Ford algorithm is run on the graph below using node \(s\) as the source.

After 2 iterations of the outer loop, which of the nodes listed below are guaranteed to have correct estimated shortest path distances (no matter the order in which graph.nodes produces the graph's nodes)? Select all that apply.

Suppose the Bellman-Ford algorithm is run on a graph \(G\) that does not contain negative cycles. Let \(u\) be an arbitrary node in the graph, and assume that \(u\) is reachable from the source.

True or False: \(u\)'s estimated distance can change multiple times during the algorithm's execution.

What is the expected time complexity of the code shown below, assuming that numbers is a Python list? Express your answer as a function of \(n\) using asymptotic notation (e.g., \(\Theta(n)\)).

def foo(numbers):
    """Assume that `numbers` is a list containing n numbers."""
    # counts is a Python dictionary, which is implemented using hash table
    counts = {}
    for x in numbers:
        for y in numbers:
            diff = abs(x - y)
            if diff not in counts:
                counts[diff] = 1
            else:
                counts[diff] = counts[diff] + 1
    return counts

foo([1, 2, 3, 4])

Suppose a hash table with \(n/2\) bins stores \(n\) elements, and suppose that when the next element is inserted into the hash table, a ``grow'' will be triggered. That is, the insertion will cause the hash table to resize to \(n\) bins containing the same \(n + 1\) elements, plus the newly-added element.

What will be the time complexity of this single insertion operation that causes the table to grow?

An undirected graph \(G = (V, E)\) has 23 nodes and 2 connected components. What is the smallest number of edges it can have?

Let \(G = (V, E)\) be an undirected graph, and suppose that \(u, v, \) and \(w\) are three nodes in \(V\). Suppose that \(u\) and \(v\) are in the same connected component, but \(u\) and \(w\) are not in the same connected component. True or False: it is possible that \(v\) and \(w\) are in the same connected component.

Let \(G\) be an undirected graph. Suppose that the degree of every node in the graph is greater than or equal to one. True or False: \(G\) must be connected.

What is the out-degree of node \(u\) in the graph shown below?

Suppose a graph \(G = (V, E)\) is stored using an adjacency list representation in the variable adj_list. What is the time complexity of the below code?

for lst in adj_list:
    for u in lst:
        print(u)

Suppose a BFS is run on the graph below using node 1 as the source node. Which node will be the BFS predecessor of node 8? You should use the convention that neighbors are produced in ascending order by label.

Suppose a ``2-chain'' graph with \(n\) nodes is constructed by taking \(n\) nodes labeled 1, 2, \(\ldots\), \(n\), and, for each node \(u\), making an edge to nodes \(u + 1\) and \(u + 2\)(if they are in the graph).

For example, such a graph with \(n = 7\) looks like:

Suppose BFS is run on a 2-chain graph with \(n\) nodes, using node 1 as the source. What is the time taken as a function of \(n\)? State your answer using asymptotic notation.

Suppose a DFS is run on the graph shown below using node 11 as the source.

What will be the DFS predecessor of node 3 in the search? Use the convention that a node's neighbors are produced in ascending order by label.

Consider the code shown below. It shows DFS as seen in lecture, with one modification: a print statement in the for-loop.

def dfs(graph, u, status=None):
    """Start a DFS at `u`."""
    # initialize status if it was not passed
    if status is None:
        status = {node: 'undiscovered' for node in graph.nodes}
    status[u] = 'pending'
    for v in graph.neighbors(u):
        print("Hello!")
        if status[v] == 'undiscovered':
            dfs(graph, v, status)
    status[u] = 'visited'

How many times will "Hello!" be printed if dfs is run on the graph below using node \(u\) as the source? Note that dfs will not be restarted if the first call does not explore the whole graph.

Suppose again that a DFS is run on the graph shown in the above problem using node 11 as the source.

In a DFS on an undirected graph \(G\), the start time of node \(u\) is 12, while the finish time of node \(u\) is 37. How many nodes were marked pending between the moment that node \(u\) was marked pending and the moment that it was marked visited? Node \(u\) itself should be excluded from your count.

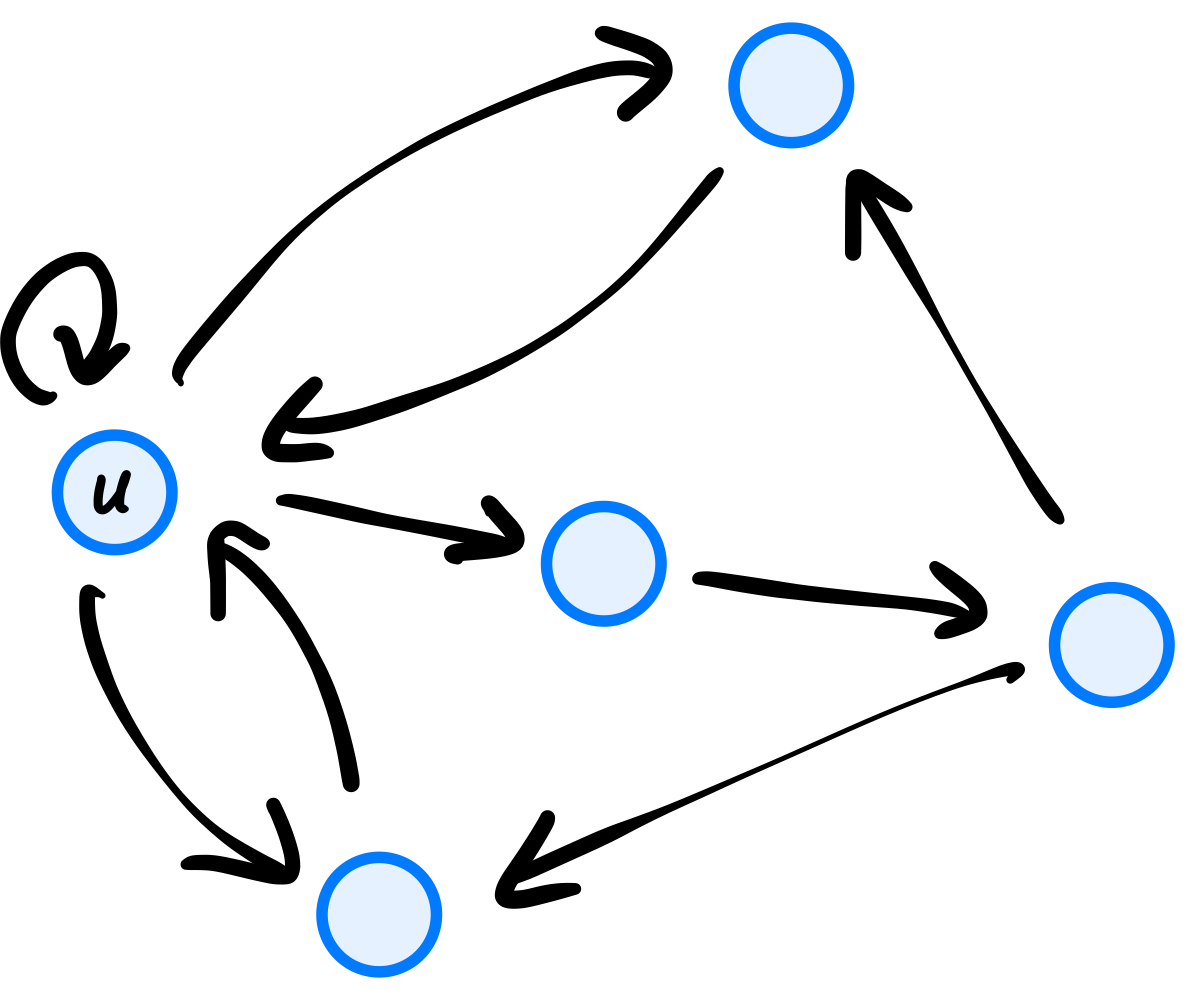
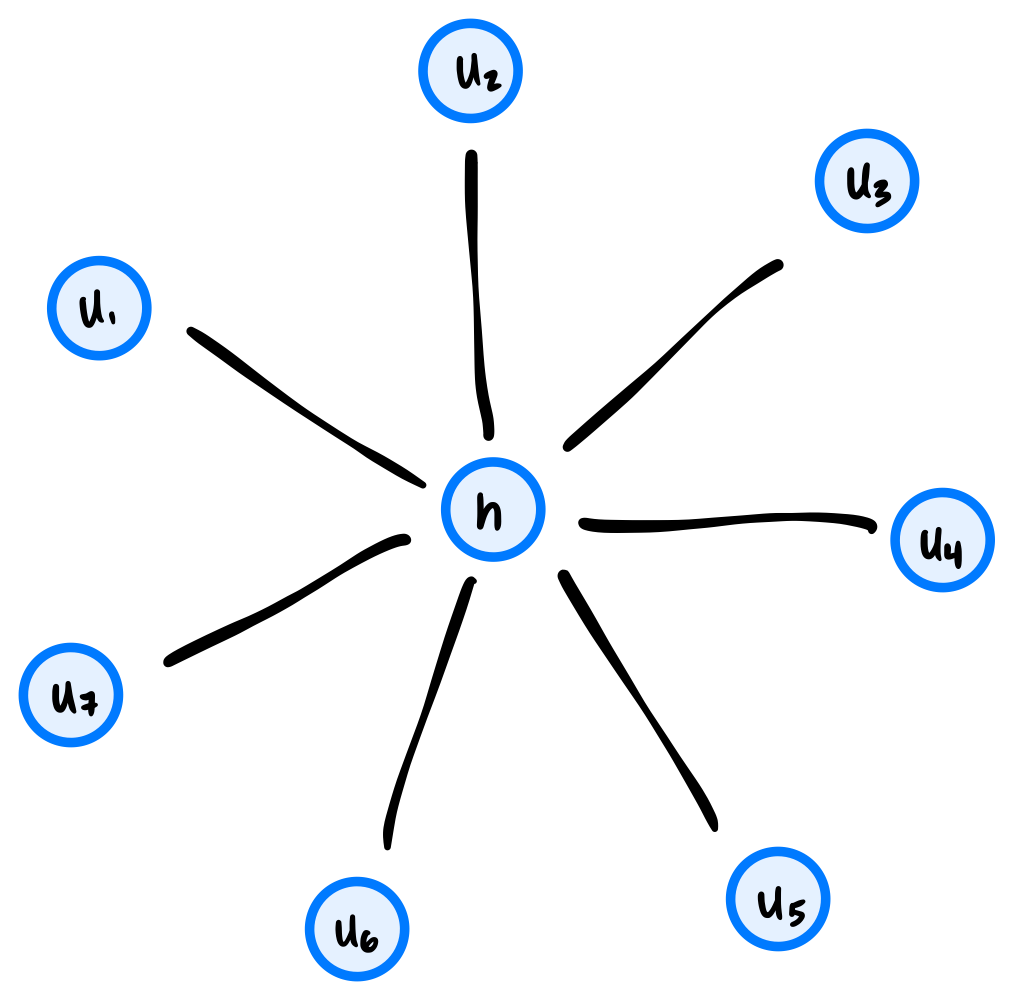
A ``hub and spoke'' graph with \(n\) nodes consists of a single ``hub'' node \(h\) along with \(n - 1\) ``spoke'' nodes, \(u_1, \ldots, u_{n-1}\) and \(n - 1\) edges from the hub node \(h\) to each of the spoke nodes. For example, a ``hub and spoke'' graph with 8 nodes looks like the below:

What is the worst case time complexity of an optimal algorithm which takes as input an arbitrary graph \(G = (V, E)\) and determines if it is a ``hub and spoke'' graph? You may assume that the graph is represented as an adjacency list and that the total number of edges in the graph can be retrieved in constant time.

Suppose the Bellman-Ford algorithm with early stopping is run on the weighted graph shown below using node \(s\) as the source (the edge weights are intentionally not shown). In the worst case, how many iterations of Bellman-Ford will be performed? That is, how many iterations of the outer for-loop will occur?

Again consider a ``2-chain'' graph, which was defined above to the a graph with \(n\) nodes that is constructed by taking \(n\) nodes labeled 1, 2, \(\ldots\), \(n\), and, for each node \(u\), making an edge to nodes \(u + 1\) and \(u + 2\)(if they are in the graph).

Suppose the Bellman-Ford algorithm without early stopping is run on a 2-chain graph with \(n\) nodes, using node 1 as the source. What is the time taken as a function of \(n\)? State your answer using asymptotic notation.

Suppose both BFS and DFS are run on the same graph \(G = (V, E)\) using the same source node. Assume that \(G\) is a tree. Consider a particular node \(u\) in the graph. True or False: the BFS predecessor found for \(u\) and the DFS predecessor found for \(u\) must be the same.

Suppose a DFS is run on a directed graph. Let \(u\) and \(v\) be two nodes in the graph, and assume that the edge \((u, v)\) exists. True or False: it is possible that, at some moment in time, \(u\) is marked as ``visited'' while \(v\) is marked as ``undiscovered''.

Let \(A\) be the adjacency matrix of the graph shown below:

Let \(\vec{a}^{(1)}\) be the first row of \(A\) and \(\vec{a}^{(2)}\) be the second row of \(A\). What is \(\vec{a}^{(1)}\cdot\vec{a}^{(2)}\)? That is, what is the dot product between the first row of \(A\) and the second row of \(A\)? Your answer should be in the form of a number.

It may help to recall that the dot product between vectors \(\vec x = (x_1, \ldots, x_d)^T\) and \(\vec y = (y_1, \ldots, y_d)^T\) is equal to \(x_1 y_1 + x_2 y_2 + \ldots + x_d y_d\).

Suppose \(T\) is a hash table of size 100 (that is, it has 100 bins). 300 elements are inserted into the hash table using a hash function that satisfies the uniform hashing assumption (that is, any element is equally-likely to hash into any bin). What is the expected number of elements in the first bin?

Suppose a hash table is constructed using linked lists to store the data within each bin, and that collisions are resolved by chaining. What is the worst case time complexity of inserting a new element into the hash table? You may assume that the hash table will not need to be resized, and that evaluating the hash function takes \(\Theta(1)\) time.

Suppose \(u\) is a node in a complete, undirected graph \(G = (V,E)\). What is the degree of \(u\)? Remember, an undirected graph is complete if it contains every possible edge.

Let \(V = \{a, b, c, d\}\) and \(E = \{(a,b), (a,a), (a,c), (d,b), (c,a)\}\) be the nodes and edges of a directed graph. How many predecessors does node \(b\) have?

Let \(C\) be a connected component in an undirected graph \(G\). Suppose \(u_1\) is a node in \(C\) and let \(u_2\) be a node that is reachable from \(u_1\). True or False: \(u_2\) must also be in the same connected component, \(C\).

Let \(A\) be the adjacency matrix representing a directed graph with $n$ nodes. What is the greatest possible sum of any row of \(A\)?

Let \(G = (V, E)\) be a connected, undirected graph with 16 nodes and 35 edges. What is the greatest possible number of edges that can be in a simple path within \(G\)?

Suppose \(G = (V, E)\) is an undirected graph. Let \(k\) be the number of connected components in \(G\). True or False: it is possible that \(k > |E|\).

Let \(G = (V, E)\) be a directed graph, and suppose \(u, v, w \in V\) are all nodes. True or False: if \(w\) is reachable from \(v\), and \(v\) is reachable from \(u\), then \(w\) is reachable from \(u\).

Let \(G = (V,E)\) be a connected, undirected graph with \(|E| = |V| - 1\). Suppose \(u\) and \(v\) are both nodes in \(G\). True or False: there can be more than one simple path from \(u\) to \(v\).

Suppose an undirected graph \(G = (V,E)\) has two connected components, \(C_1\) and \(C_2\). Suppose that \(|C_1| = 4\) and \(|C_2| = 3\). What is the largest that \(|E|\) can possibly be?

Suppose a breadth first search (BFS) is run on the graph shown below using node \(u_4\) as the source and the convention that graph.neighbors produces nodes in ascending order by label. What will be the predecessor of \(u_6\) in the BFS?

Suppose a depth first search (DFS) is run on the graph shown below using node \(u_4\) as the source and the convention that graph.neighbors produces nodes in ascending order by label. What will be the predecessor of \(u_6\) in the DFS?

Suppose a breadth first search (BFS) is run on a graph \(G = (V, E)\), and that node \(u\) is distance 5 from the source while node \(v\) is distance 3 from the source. True or False: it is possible that at some point during the BFS, both \(u\) and \(v\) are in the pending queue at the same time.

Suppose the code below is run on a graph \(G = (V, E)\). What is its time complexity? You may assume that \(|E| \geq 1\).

for u in graph.nodes:
    for v in graph.neighbors(u):
        print(u, v)

What is the time complexity of depth first search (DFS) when run on a tree with \(n\) nodes?

Suppose a depth first search is run on a directed graph. True or False: it is possible that, at any moment in time, there is a node marked as visited which has a neighbor (successor) that is marked as pending.

Suppose a depth first search is run on the graph shown below using node \(u_4\) as the source, and adopt the convention that graph.neighbors produces nodes in ascending order of label. Which node will have the smallest finish time?

Suppose a depth first search is run on the graph shown below using node \(u_4\) as the source, and adopt the convention that graph.neighbors produces nodes in ascending order of label. What will be the start time of node \(u_7\)?

Let \(G = (V,E)\) be the directed graph with \(V = \{a, b, c, d, e\}\) and \(E = \{(a, b), (a, c), (a, d), (b, e), (c, e), (d, e)\}\). How many valid topological sorts of $V$ are there?

Suppose \(T = (V, E)\) is a connected, undirected graph with no cycles (that is, \(T\) is a tree). Suppose a depth first search is run on \(T\) using node s as the source. Assume that node s has two neighbors: \(u\) and \(v\). If \(|V| = 15\), which one of the below represents possible start and finish times of \(u\) and \(v\)? You may assume that graph.neighbors produces neighbors in ascending order of label.

Recall that Bellman-Ford with early stopping updates edges iteratively until no estimated distances change, at which point the algorithm terminates early. True or False: the number of iterations needed before early termination may depend on the order in which the edges are updated.

Suppose that every edge in the weighted graph \(G\) has weight -5. True or False: breadth first search on this graph will compute a longest path from the source to every node in the graph (that is, a path with greatest possible total edge weight).

You may assume that every node in the graph is reachable from the source.