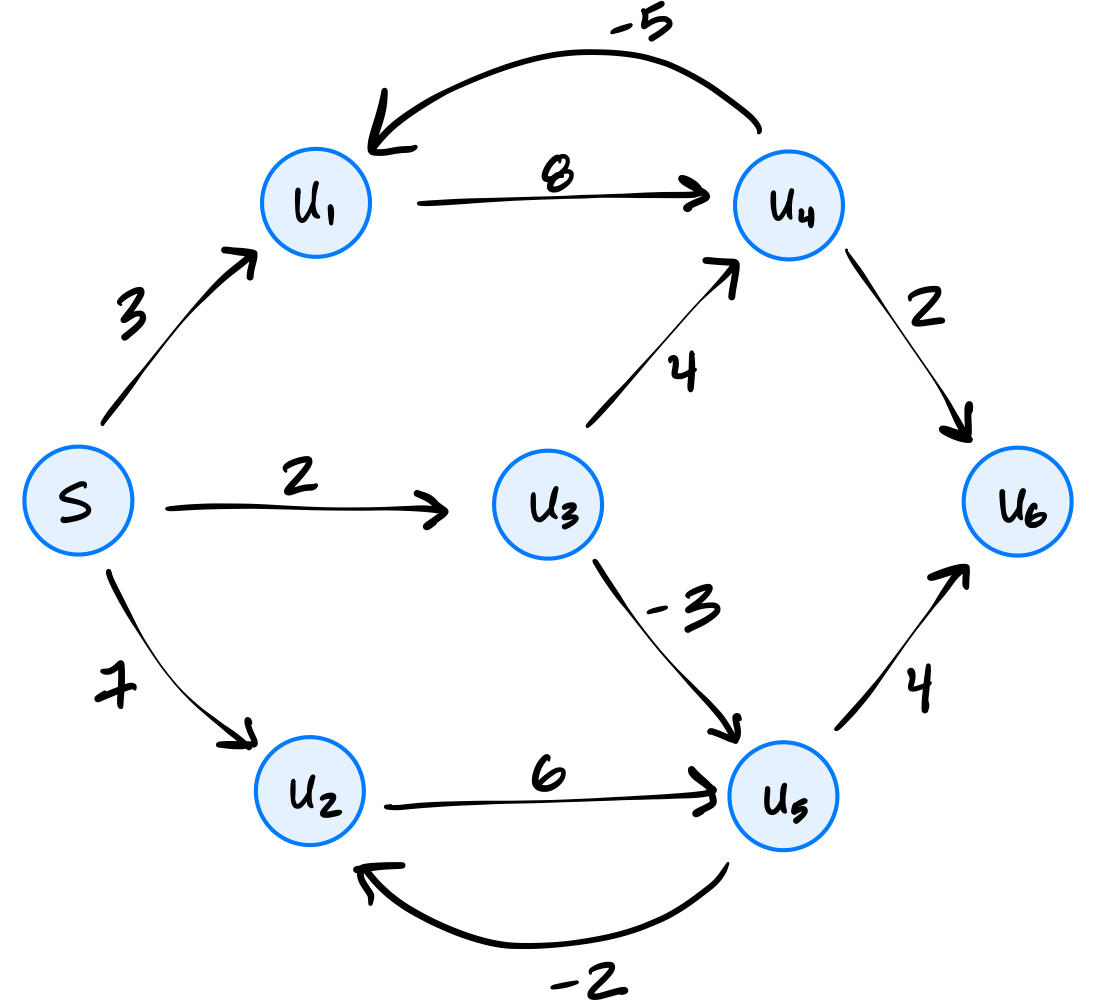
Problems tagged with "bellman-ford"

Recall that the outer loop of the Bellman-Ford algorithm without early stopping loops for a fixed number of iterations, while the inner loop iterates over each edge of the graph.

Suppose Bellman-Ford with early stopping is run on the graph below using node \(s\) as the source:

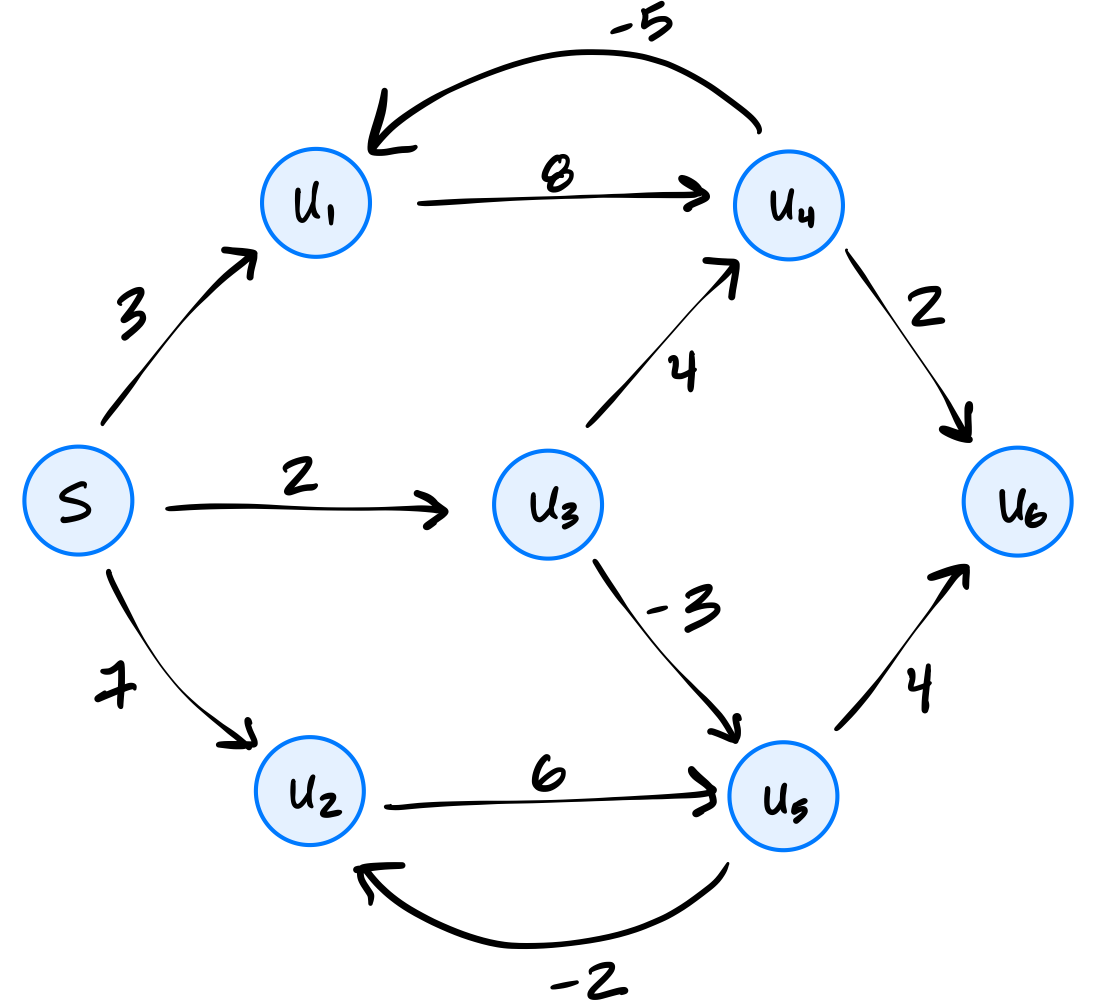
What is the fewest number of iterations of the outer loop that can possibly be performed?

Recall that the Bellman-Ford algorithm keeps track of the estimated shortest path distance from the source to each node in the graph. These estimates are updated, and eventually become correct, provided that the graph has no negative cycles.

Suppose the Bellman-Ford algorithm is run on the graph below using node \(s\) as the source.

After 2 iterations of the outer loop, which of the nodes listed below are guaranteed to have correct estimated shortest path distances (no matter the order in which graph.nodes produces the graph's nodes)? Select all that apply.

Suppose the Bellman-Ford algorithm is run on a graph \(G\) that does not contain negative cycles. Let \(u\) be an arbitrary node in the graph, and assume that \(u\) is reachable from the source.

True or False: \(u\)'s estimated distance can change multiple times during the algorithm's execution.

Suppose the Bellman-Ford algorithm with early stopping is run on the weighted graph shown below using node \(s\) as the source (the edge weights are intentionally not shown). In the worst case, how many iterations of Bellman-Ford will be performed? That is, how many iterations of the outer for-loop will occur?

Again consider a ``2-chain'' graph, which was defined above to the a graph with \(n\) nodes that is constructed by taking \(n\) nodes labeled 1, 2, \(\ldots\), \(n\), and, for each node \(u\), making an edge to nodes \(u + 1\) and \(u + 2\)(if they are in the graph).

Suppose the Bellman-Ford algorithm without early stopping is run on a 2-chain graph with \(n\) nodes, using node 1 as the source. What is the time taken as a function of \(n\)? State your answer using asymptotic notation.

Recall that Bellman-Ford with early stopping updates edges iteratively until no estimated distances change, at which point the algorithm terminates early. True or False: the number of iterations needed before early termination may depend on the order in which the edges are updated.