Link Search Menu Expand Document
DSC 90

Week 1 – Introduction, Calculus

Welcome to the first lecture and week of DSC 90 this quarter! Each week of DSC 90 will have a webpage, like this one, that contains links to lecture slides, recordings, and required readings, and also contains that week’s homework assignment.

Lecture (January 3rd) 👨‍🏫

Readings 📖

Required:

Optional:

Homework 1 (due Sunday, January 9th at 11:59PM) (solutions) 📝

Welcome to your first DSC 90 homework! Homeworks in DSC 90 are designed to have you engage with the week’s content. They will rely on you having completed the readings.

Submit your answers as a PDF to Gradescope by the due date for full credit. We encourage you to discuss the readings and questions with others in the course, but all work must be your own. Remember to use Campuswire if you need guidance!


Question 1

For both subparts, we’re expecting 3-4 sentences.

(a) According to Donoho, in “The Future of Data Analysis”, John Tukey stated that the science of data analysis is being shaped by four factors. In your own words, what are those four factors?

(b) Based on your current understanding, describe how the field of data science is different than the field of statistics.

Question 2

Disclaimer: This question looks long, but the amount of work you’ll have to do is relatively minimal.

Archimedes’ approximation for the value of \(\pi\) used the fact that the ratio between the circumference of a circle and the diameter of that circle is constant.

Suppose we are given that \(\pi\) is also equal to the ratio between the area of a circle and the square of the radius of that circle. (This is not a trivial fact, but we will use it without proof for now.) What if we try to estimate \(\pi\) using this fact, instead? That is, what if we inscribe regular polygons with more and more sides inside a circle with radius \(r = 1\), and estimate \(\pi\) with

\[\pi \approx \frac{\text{Area of regular n-gon}}{r^2} = \text{Area of regular n-gon}\]

(The term “\(n\)-gon” refers to a polygon with \(n\) sides.)

Intuitively, as our inscribed polygon has more and more sides, it looks more and more like a circle, so its area should approach the area of the circle. (This is not a fully rigorous argument, but it will suffice for our purposes.)

Recall from lecture, if \(s_1\) is the side length of a regular \(n\)-gon inscribed in a circle of radius 1 and \(s_2\) is the side length of a regular \(2n\)-gon inscribed in the same circle, then

\[s_2 = \sqrt{\left(\frac{s_1}{2}\right)^2 + \left( 1 - \sqrt{1 - \left(\frac{s_1}{2}\right)^2} \right)^2}\]

(This formula is implemented by next_sidelength(s) in the code for this week’s lecture.)

Since we already have this formula, we’re already able to calculate the side length of a regular \(n\)-gon for any value of \(n\) in the sequence (6, 12, 24, 48, 96, 192, …), which are the same polygons we’ll continue to look at.

Now, let’s switch our focus to calculating the area of a given inscribed \(n\)-gon. Let’s supppose our \(n\)-gon has side length \(s\). Then, one way to calculate its area is to split the \(n\)-gon into \(n\) isoceles triangles, each of which have two sides of length \(r = 1\) and one side of length \(s\). What we then need to do is find the area of one of these isoceles triangles and multiply it by \(n\).

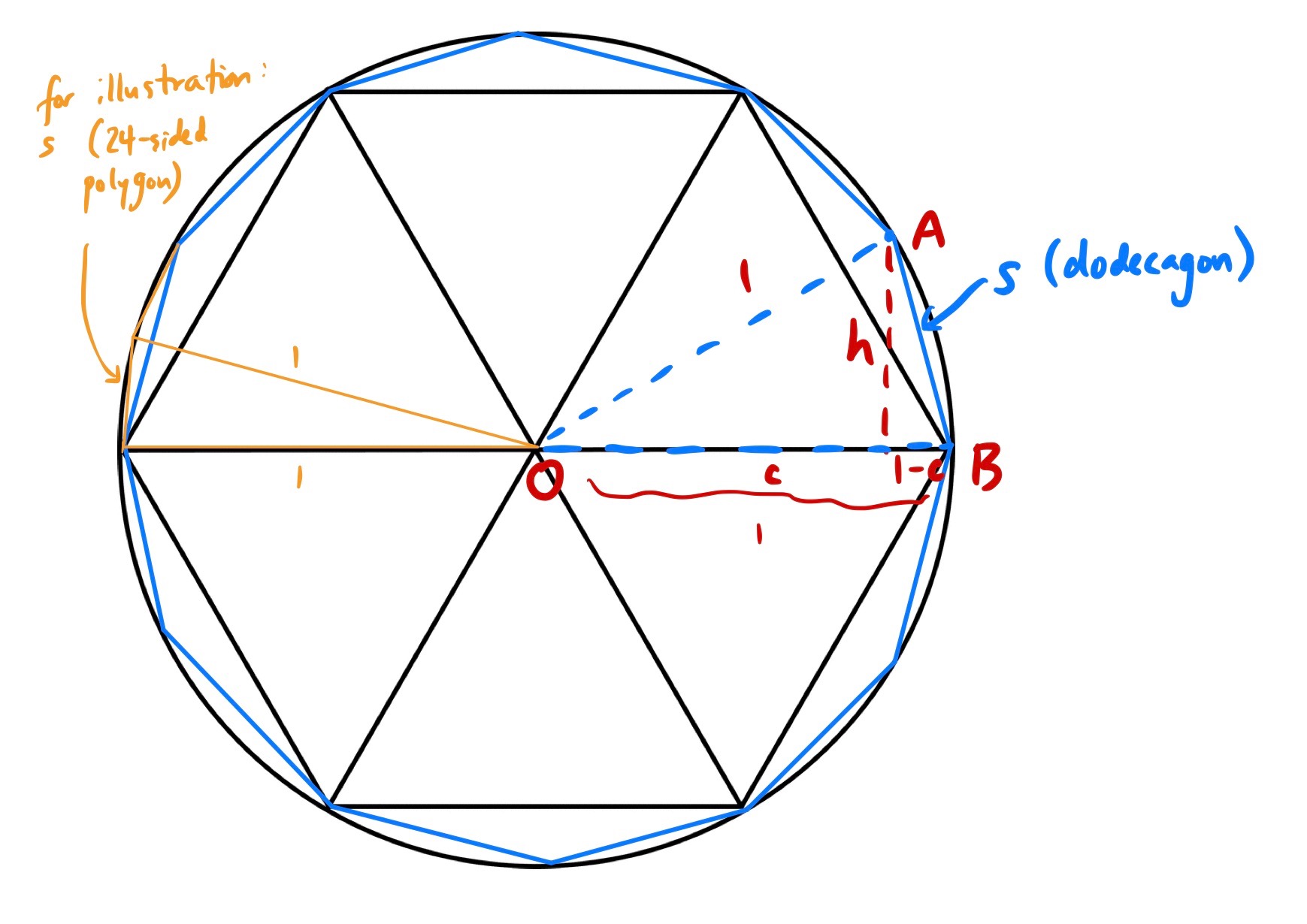
In the image above, the blue polygon is a dodecagon, a regular polygon with 12 sides. If we find the area of triangle OAB and multiply it by 12, we’ll get the area of the dodecagon. (Similarly, if we found the area of the orange triangle and multiplied it by 24, we’d get the area of the inscribed 24-sided polygon. Note that the orange triangle also has two sides of length 1.)

To find the area of triangle OAB, we need to multiply its base (which we know to be 1) by its height, which we’ve denoted as \(h\) in the diagram above, and divide the result by 2. Our problem now lies in determining what \(h\) is, in terms of \(s\). (Remember, for any value of \(n\), we know \(s\).)

(a) Use the above diagram and the Pythagorean Theorem to find two equations that involve some or all of \(h\), \(c\), and \(s\), and show that

\[h = \sqrt{1 - \left( 1 - \frac{s^2}{2} \right)^2}\]

Show your work.

(b) Open the lecture notebook, linked at the top of this page. Add two new cells above the cell that contains the text “Let’s do some calculations.”

  1. In the first cell, define a function height(s) that implements the relationship between \(h\) and \(s\) we found in part \(a\).
    • Check: height(1) should return approximately 0.86602540378. (The exact value of this is \(\frac{\sqrt{3}}{2}\).)
  2. In the second cell, define a function pi_estimate_area(h, n) which takes in a value of \(h\) (as defined above) and \(n\) (the number of sides) and returns the area of the inscribed regular \(n\)-gon. The body of your function should only be one relatively straightforward line of code.
    • Check: pi_estimate_area(height(1), 6) should return approximately 2.5980762113. This is computing the area of a regular hexagon with side length 1; the exact value of this is \(\frac{3 \sqrt{3}}{2}\).
  3. Now, in the cell containing the for-loop, add a line that computes the value of h for the current s (before the print statement), and replace pi_estimate(s, n) with pi_estimate_area(h, n). Run the cell.

You’ve now estimated the value of \(\pi\) using the areas of inscribed polygons rather than the perimeters of inscribed polygons. Nice work! In your PDF writeup, provide a screenshot of all of the code you wrote and the output of the new for-loop.

(c) Which method seems like it converges to \(\pi\) quicker – the method based on perimeters, or the method based on areas?

Question 3

After finishing Questions 1 and 2, but before submitting the homework, please fill out this anonymous survey. Once you submit the survey, it’ll show you a secret word. Write that secret word in your PDF as the answer to Question 3. Thanks!

(Optional) Question 4

Watch this video on YouTube: How to Calculate Pi, Archimedes’ Method.

This video describes a process similar to the one we covered in class, but with a few key differences. What are the differences between this approach and the approach from class? Do you think this approach is historically accurate (i.e. could this have been the approach Archimedes used)?

If you answer this question, assign it to Question 3 on Gradescope when matching pages.